【机器学习】EM算法从小白到理解,附带案例代码
前言
\quad\quad 本篇主要介绍 EM算法 相关内容,首先通过极大似然估计引出 EM算法 的作用,然后通过例子引出 EM算法 ,旨在尽可能的通俗易懂地让大家理解 EM算法 ,最后在介绍 EM算法 算法在高斯混合模型(GMM)中的应用,通过Python实现。
\quad\quad 学习机器学习必定会碰到 EM算法,博主希望通过本篇可以帮助到大家,因为博主也在学习中,所以难免会有错误的地方,还望大家多多指教!
本篇代码可见:Github
一、最大似然估计
学习过数理统计的知道,在参数模型中,最大似然估计法(MLE)是一种参数估计方法,其思想如下:
在没有其他信息的情况下,我们只能认为在一次
随机试验中发生的事件具有最大的概率。反过来,如果能够使事件发生的概率最大化,那么该事件也就最有可能发生,因此寻找使概率最大化的参数就是很自然的想法了,最大似然估计法就是基于这样的思想。“似然”在这里就是“可能是”的意思。
1、定义似然函数
-
假设总体 X X X 是离散总体,其概率分布为 P ( X = x ; θ ) P(X=x;\theta) P(X=x;θ) 记为 f ( x ; θ ) f(x;\theta) f(x;θ),当给定 θ \theta θ 时, f ( x ; θ ) f(x;\theta) f(x;θ) 为 X X X 在 x x x 处发生的概率, ∏ i = 1 n f ( x i ; θ ) \prod_{i=1}^n f(x_i;\theta) ∏i=1nf(xi;θ) 为样本 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn 在点 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 处发生的概率(联合概率)。当固定 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 时,让 θ \theta θ 变化,可能存在某个 θ \theta θ 使得概率 ∏ i = 1 n f ( x i ; θ ) \prod_{i=1}^n f(x_i;\theta) ∏i=1nf(xi;θ) 达到最大,记为 θ ^ \hat{\theta} θ^,显然它是 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 的函数,即选择的参数 θ ^ \hat{\theta} θ^ 是使概率 ∏ i = 1 n f ( x i ; θ ) \prod_{i=1}^n f(x_i;\theta) ∏i=1nf(xi;θ) 达到最大的最值点,因此称 θ ^ ( X 1 , X 2 , . . . , X n ) \hat{\theta}(X_1,X_2,...,X_n) θ^(X1,X2,...,Xn) 是参数 θ \theta θ 的最大似然估计值。
-
如果总体 X X X 是连续型的,则样本 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn 在点 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 处发生的概率近似为 ∏ i = 1 n f ( x i ; θ ) Δ x i \prod_{i=1}^n f(x_i;\theta)\Delta x_i ∏i=1nf(xi;θ)Δxi,由于 Δ x i \Delta x_i Δxi 与参数 θ \theta θ 无关,所以 ∏ i = 1 n f ( x i ; θ ) Δ x i \prod_{i=1}^n f(x_i;\theta)\Delta x_i ∏i=1nf(xi;θ)Δxi 与 ∏ i = 1 n f ( x i ; θ ) \prod_{i=1}^n f(x_i;\theta) ∏i=1nf(xi;θ) 关于 θ \theta θ 具有相同的最大值点。
因此,定义 似然函数 为:
L ( θ ; x 1 , x 2 , . . . x n ) = ∏ i = 1 n f ( x i ; θ ) L(\theta;x_1,x_2,...x_n) = \prod_{i=1}^n f(x_i; \theta) L(θ;x1,x2,...xn)=i=1∏nf(xi;θ)
其中 L ( θ ; x 1 , x 2 , . . . x n ) L(\theta;x_1,x_2,...x_n) L(θ;x1,x2,...xn) 表示当给定样本观测值 x 1 , x 2 , . . . , x n x_1, x_2,...,x_n x1,x2,...,xn 时仅为 θ \theta θ 的函数。
2、最大似然估计
θ \theta θ 的 最大似然估计 定义为满足:
L ( θ ^ ; x 1 , x 2 , . . . , x n ) = max θ ∈ Θ L ( θ ; x 1 , x 2 , . . . x n ) L(\hat{\theta};x_1,x_2,...,x_n) = \max_{\theta \in \Theta} L(\theta;x_1,x_2,...x_n) L(θ^;x1,x2,...,xn)=θ∈ΘmaxL(θ;x1,x2,...xn) 的统计量 θ ^ ( X 1 , X 2 , . . . , X n ) \hat{\theta}(X_1,X_2,...,X_n) θ^(X1,X2,...,Xn)。
3、似然方程
利用极值原理,假设似然函数 L ( θ ; x 1 , x 2 , . . . x n ) L(\theta;x_1,x_2,...x_n) L(θ;x1,x2,...xn) 关于 θ \theta θ 连续可微,令其偏导数为0:
∂ ∂ θ L ( θ ; x 1 , x 2 , . . . x n ) = 0 \frac{\partial}{\partial \theta} L(\theta;x_1,x_2,...x_n) = 0 ∂θ∂L(θ;x1,x2,...xn)=0
其中:
i = ( 1 , 2 , . . . , k ) θ = ( θ 1 , θ 2 , . . . , θ k ) i = (1, 2, ... ,k) \quad\quad \theta=(\theta_1, \theta_2, ..., \theta_k) i=(1,2,...,k)θ=(θ1,θ2,...,θk)
上面方程通常称为似然方程。
由于似然函数是函数相乘的,为了计算方便,我们常常取对数似然函数,很容易知道: L ( θ ; x 1 , x 2 , . . . x n ) L(\theta;x_1,x_2,...x_n) L(θ;x1,x2,...xn) 和 ln L ( θ ; x 1 , x 2 , . . . x n ) \ln L(\theta;x_1,x_2,...x_n) lnL(θ;x1,x2,...xn) 在参数空间 Θ \Theta Θ 上具有相同的最大值点,因此似然方程可改写为:
∂ ∂ θ ln L ( θ ; x 1 , x 2 , . . . x n ) = 0 \frac{\partial}{\partial \theta} \ln L(\theta;x_1,x_2,...x_n) = 0 ∂θ∂lnL(θ;x1,x2,...xn)=0
通过求解上式得到 θ i ( x 1 , x 2 , . . . x n ) ( i = 1 , 2 , . . . , k ) \theta_i(x_1, x_2,...x_n)(i = 1,2,...,k) θi(x1,x2,...xn)(i=1,2,...,k),记为 θ ^ i ( x 1 , x 2 , . . . , x n ) \hat{\theta}_i(x_1, x_2, ..., x_n) θ^i(x1,x2,...,xn),并称之为参数 θ 1 , θ 2 , . . θ k \theta_1, \theta_2, .. \theta_k θ1,θ2,..θk 的最大似然估计值。
4、例子解释
\quad\quad 随机选择 n n n 个男生,我们知道人的身高是满足正态分布的,假设样本 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn 来自正态分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2),其中参数 μ , σ 2 \mu, \sigma^2 μ,σ2是未知的,求参数 μ , σ 2 \mu, \sigma^2 μ,σ2 的最大似然估计量 μ , σ 2 \mu, \sigma^2 μ,σ2。
解:因为总体满足正态分布,所以总体的密度函数为:
f ( x ; μ , σ 2 ) = 1 2 π σ e x p ( − ( x − μ ) 2 2 σ 2 ) f(x;\mu, \sigma^2) = \frac{1}{\sqrt {2\pi} \sigma} exp({-\frac{(x-\mu)^2}{2\sigma^2}}) f(x;μ,σ2)=2πσ1exp(−2σ2(x−μ)2)
由似然函数的定义得:
L ( μ , σ 2 ; x 1 , x 2 , . . . , x n ) = ∏ i = 1 n f ( x i ; μ , σ 2 ) L(\mu, \sigma^2;x_1,x_2,...,x_n) = \prod_{i=1}^n f(x_i; \mu, \sigma^2) L(μ,σ2;x1,x2,...,xn)=i=1∏nf(xi;μ,σ2)
= ∏ i = 1 n 1 2 π σ e x p ( − ( x i − μ ) 2 2 σ 2 ) =\prod_{i=1}^n \frac{1}{\sqrt {2\pi} \sigma} exp({-\frac{(x_i-\mu)^2}{2\sigma^2}}) =i=1∏n2πσ1exp(−2σ2(xi−μ)2)
= ( 1 2 π σ 2 ) n 2 e x p ( − ∑ i = 1 n ( x i − μ ) 2 2 σ 2 ) =(\frac{1}{2\pi \sigma^2})^{\frac{n}{2}}exp(-\frac{\sum_{i=1}^n (x_i - \mu)^2}{2 \sigma^2}) =(2πσ21)2nexp(−2σ2∑i=1n(xi−μ)2)
两边取对数,得:
ln L ( μ , σ 2 ; x 1 , x 2 , . . . , x n ) = − n 2 ln ( 2 π σ 2 ) − ∑ i = 1 n ( x i − μ ) 2 2 σ 2 \ln L(\mu, \sigma^2;x_1,x_2,...,x_n) = -\frac{n}{2} \ln(2\pi\sigma^2)-\frac{\sum_{i=1}^n (x_i - \mu)^2}{2 \sigma^2} lnL(μ,σ2;x1,x2,...,xn)=−2nln(2πσ2)−2σ2∑i=1n(xi−μ)2
对参数 ( μ , σ 2 (\mu, \sigma^2 (μ,σ2 分别求导,得到似然方程:
{ ∂ ∂ μ ln L ( μ , σ 2 ; x 1 , x 2 , . . . , x n ) = 1 σ 2 ∑ i = 1 n ( x i − μ ) 2 = 0 ∂ ∂ σ 2 ln L ( μ , σ 2 ; x 1 , x 2 , . . . , x n ) = − n 2 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 0 \begin{cases} \frac{\partial}{\partial \mu} \ln L(\mu, \sigma^2;x_1,x_2,...,x_n) = \frac{1}{\sigma^2}\sum_{i=1}^n(x_i - \mu)^2 = 0 \\ \\ \frac{\partial}{\partial \sigma^2} \ln L(\mu, \sigma^2;x_1,x_2,...,x_n) =-\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_{i=1}^n(x_i - \mu)^2 = 0 \end{cases} ⎩⎪⎨⎪⎧∂μ∂lnL(μ,σ2;x1,x2,...,xn)=σ21∑i=1n(xi−μ)2=0∂σ2∂lnL(μ,σ2;x1,x2,...,xn)=−2σ2n+2σ41∑i=1n(xi−μ)2=0
解得:
{ μ = 1 n ∑ i = 1 n x i σ 2 = 1 n ∑ i = 1 n ( x i − x ‾ ) 2 \begin{cases} \mu = \frac{1}{n}\sum_{i=1}^n x_i \\ \\ \sigma^2 = \frac{1}{n}\sum_{i=1}^n(x_i - \overline{x})^2 \end{cases} ⎩⎪⎨⎪⎧μ=n1∑i=1nxiσ2=n1∑i=1n(xi−x)2
所以参数 μ , σ 2 \mu, \sigma^2 μ,σ2 的最大似然估计量为 μ ^ = 1 n ∑ i = 1 n x i \hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i μ^=n1∑i=1nxi, σ 2 ^ = 1 n ∑ i = 1 n ( x i − x ‾ ) 2 \hat{\sigma^2} = \frac{1}{n}\sum_{i=1}^n(x_i - \overline{x})^2 σ2^=n1∑i=1n(xi−x)2。
5、求极大似然估计量的一般步骤
- 写出似然函数;
- 取对数似然函数,并整理;
- 求导数,令导数为0,得到似然方程;
- 求解似然方程,得到的参数即为所求;
\quad\quad 通过以上分析,我们可以知道极大似然估计(MLE)就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值的计算过程。简单地说,就是给定了一定的数据,假定知道数据是从某种分布中随机抽取出来的,但是不知道这个分布的具体的参数值,即“模型已定,参数未知”,MLE就可以用来估计模型的参数。MLE的目标是找出一组参数(模型中的参数),使得模型产出数据的概率最大。
二、引出 EM算法
现在我们已经知道,极大似然估计就是:知道模型,反推参数。
\quad\quad 下面我们将上面的例子进一步延伸,前面我们只随机选取了 n n n 个男生,这次我们随机选取 100 个 男生和 100 个女生,他/她们的身高组成样本集 X = ( X 1 , X 2 , . . . , X n ) ( n = 200 ) X = (X_1, X_2, ...,X_n) (n =200) X=(X1,X2,...,Xn)(n=200) ,假定男生的身高服从正态分布: N ( μ 1 , σ 1 2 ) N(\mu_1, \sigma_1^2) N(μ1,σ12),女生的身高服从另一个正态分布: N ( μ 2 , σ 2 2 ) N(\mu_2, \sigma_2^2) N(μ2,σ22),但是我们不知道具体的模型参数 μ , σ 2 \mu,\sigma^2 μ,σ2,现在我们的目标就是求未知的模型参数。
1、思考
\quad\quad 这个例子也是:知道模型,反推参数,但是我们发现此时有两个模型的参数需要求,而极大似然估计法中的概率分布只有一个或者我们知道上面的样本哪个是男生哪个是女生(即:知道样本是通过哪个概率分布得到的),只不过我们不知道这个概率分布的参数,此时求解只需要根据模型对应的样本求解相应模型的参数,分别进行类似的求解就可以得到两个模型的参数。
\quad\quad 但是现在这100个男生和100个女生混合在一起了,我们并不知道每个样本是来自哪个概率分布,这个时候样本来自哪个概率分布就成了一个 隐变量 (本例也就是样本是男生还是女生)。
通常来说,我们只有知道了精确的男女生身高的正态分布参数,我们才能知道每一个人更有可能是男生还是女生。反过来,我们只有知道了每个人是男生还是女生,才能尽可能准确地估计男女各自身高的正态分布的参数。
EM算法 便是为了解决上面使用“极大似然估计法”存在的缺陷(含有隐变量)。
2、什么是 EM算法 ?
EM算法(Expectation-maximization Algorithm,最大期望算法或期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量:
EM算法 经过两个步骤交替进行计算,是一种迭代算法:
- E:计算期望,利用对隐变量的现有估计值,计算其最大似然估计值;
- M:最大化,最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
3、隐变量
\quad\quad 我们知道,EM算法 和 极大似然估计法 区别就在于 EM算法 多了隐变量,那么理解 EM算法 中的隐变量便成了关键。
通常,我们用 Y Y Y 表示观测到的随机变量的数据(如上面例子中样本的身高), Z Z Z 表示隐随机变量的数据(如上面例子中观测不到样本是从哪个概率分布中得到的,所以这个叫做隐变量。
- 完全数据: Y Y Y 和 Z Z Z 连在一起
- 不完全数据:仅 Y Y Y 一个
EM算法 面临的主要主要问题就是:有个隐变量数据 Z Z Z ,如果 Z Z Z 已知的话,那么问题就可以通过极大似然估计求解了。那么 EM算法 又是怎么处理这个问题的呢?我们举个例子来说明:
假定你是一个幼儿园老师,有一杯牛奶,现在需要把牛奶
平均分配给表现优秀的小朋友。如果只有一个表现优秀小朋友那都给他就好了,但是如果有两个表现优秀的小朋友,由于我们不知道到底每个小朋友应该分多少牛奶,所以无法一次性把牛奶平均分配。
相信大家的做法都可以描述如下:
- 先拿两个杯子,将牛奶随意地分到两个杯子,然后看看哪个杯子中的牛奶多,就把多的杯子往少的杯子中匀一点,之后重复多次这个过程,直到两个杯子中的牛奶一样多。
上面的例子中,平均分配这个果可以看作“观测数据”,为了达到平均分配而给每个杯子分配多少牛奶可以看作“待求参数”,每次比较后匀一点的手感可以看作是“概率分布”。
如果只有一个表现优秀的小朋友,那么概率分布就确定了(就是把牛奶都倒到这个小朋友的杯子里),但是因为有两个表现优秀的小朋友,所以我们无法一次就能够平均分配,不过可以采用上面描述的方式来实现最终的目标。
4、EM算法的思想
- 给参数 θ \theta θ 自主初始化个初值(如:既然我们不知道要平均分配牛奶到两个杯子,两个杯子到底要分配多少,那我们可以先估计这个值);
- 根据给定观测数据和当前的参数 θ \theta θ,求未观测数据的条件概率分布的期望(如:在上一步中,已经根据初值的概率分布将牛奶分配到两个杯子,然后这一步根据“比较两个杯子各有多少牛奶”来判断此次分配的结果)
- 上一步中未观测数据已经求出来了,于是根据极大似然估计求最优的参数 θ ^ \hat{\theta} θ^(上一步中既然分配结果已经有了,那么就根据概率分布判断下杯子里应该有多少牛奶,然后把牛奶匀一下)
- 因为第二步和第三步的结果可能不是最优的,所以重复第二步和第三步,直到收敛(重复多次匀一点的操作,直到两个杯子的牛奶大致一样多)
5、例子解释
有两个硬币 A A A 和 B B B,假设随机抛硬币后正面朝上的概率分别为 P A , P B P_A,P_B PA,PB,为了顾及这两个硬币正面朝上的概率,我们轮流抛硬币 A A A 和 B B B,每一轮都连续抛5次,总共5轮,观测结果如下:
| 硬币 | 结果 | 统计 |
|---|---|---|
| A | 正正反正反 | 3正-2反 |
| B | 反反正正反 | 2正-3反 |
| A | 正反反反反 | 1正-4反 |
| B | 正反反正正 | 3正2反 |
| A | 反正正反反 | 2正-3反 |
根据上表数据,我们知道A硬币抛了15次,B硬币抛了10次,很容易求得:
P A = ( 3 + 1 + 2 ) / 15 = 0.4 P_A = (3+1+2) / 15 = 0.4 PA=(3+1+2)/15=0.4
P B = ( 2 + 3 ) / 10 = 0.5 P_B = (2+3) / 10 = 0.5 PB=(2+3)/10=0.5
当然,这个结果并不能完全说明 P A , P B P_A,P_B PA,PB ,但是要是试验的次数足够多,根据“大数定理”,这个值可以无限接近真实的 P A , P B P_A,P_B PA,PB。
问题来了,要是我们不知道每轮抛的硬币是A还是B呢?然后再轮流抛5轮,观测结果如下:
| 硬币 | 结果 | 统计 |
|---|---|---|
| 未知 | 正正反正反 | 3正-2反 |
| 未知 | 反反正正反 | 2正-3反 |
| 未知 | 正反反反反 | 1正-4反 |
| 未知 | 正反反正正 | 3正2反 |
| 未知 | 反正正反反 | 2正-3反 |
我们要求的目标没有变,还是求:硬币A和B正面朝上的概率 P A , P B P_A,P_B PA,PB。
此时,该问题就多了一个硬币种类的隐变量,设为 Z = ( z 1 , z 2 , z 3 , z 4 , z 5 ) Z=(z_1,z_2,z_3,z_4,z_5) Z=(z1,z2,z3,z4,z5),代表每轮抛硬币所使用的硬币是A还是B
- 其中这个隐变量 Z Z Z 我们是不知道,就无法估计 P A , P B P_A,P_B PA,PB,所以我们必须先估计出 Z Z Z ,然后才能进一步估计 P A , P B P_A,P_B PA,PB;
- 但是要估计 Z Z Z ,我们又要知道 P A , P B P_A,P_B PA,PB,这样我们才能用极大似然估计法去估计 Z Z Z,那么这不就是鸡生蛋和蛋生鸡的问题了吗?那么又该如何解决呢?
答案就是:先随机初始化一个 P A , P B P_A,P_B PA,PB,用它来估计 Z Z Z ,然后基于 Z Z Z ,还是按照极大似然估计法去估计新的 P A , P B P_A,P_B PA,PB,如果新的 P A , P B P_A,P_B PA,PB和我们初始化的 P A , P B P_A,P_B PA,PB一样,那么说明:我们初始化的值是一个相当靠谱的估计!也就是说,我们初始化的 P A , P B P_A,P_B PA,PB,按照最大似然估计法可以估计出 Z Z Z ,然后基于 Z Z Z ,按照最大似然估计法可以反过来估计出 P 1 , P 2 P_1,P_2 P1,P2,当 P 1 , P 2 P_1,P_2 P1,P2和 P A , P B P_A,P_B PA,PB一样时,说明 P 1 , P 2 P_1,P_2 P1,P2 很有可能就是真实的值。如果新估计出来的 P A , P B P_A,P_B PA,PB 和我们初始化的值差别很大,就继续使用新的 P A , P B P_A,P_B PA,PB进行迭代,直到收敛。
不妨假设, P A = 0.2 , P B = 0.7 P_A = 0.2,P_B=0.7 PA=0.2,PB=0.7;然后我们看第一轮抛掷的最可能的是哪个硬币:
- 如果是硬币A,得出3正2反的概率为:
0.2 ∗ 0.2 ∗ 0.2 ∗ 0.8 ∗ 0.8 = 0.00512 0.2*0.2*0.2*0.8*0.8 = 0.00512 0.2∗0.2∗0.2∗0.8∗0.8=0.00512 - 如果是硬币B,得出3正2反的概率为:
0.7 ∗ 0.7 ∗ 0.7 ∗ 0.3 ∗ 0.3 = 0.03087 0.7*0.7*0.7*0.3*0.3 = 0.03087 0.7∗0.7∗0.7∗0.3∗0.3=0.03087
然后依次求出其他四轮的相应概率,如下表:
| 轮数 | 若是硬币A | 若是硬币B | 按照最大似然法则 |
|---|---|---|---|
| 1 | 3正-2反——0.00512 | 3正-2反——0.03087 | 最有可能的是硬币B |
| 2 | 2正-3反——0.02048 | 2正-3反——0.01323 | 最有可能的是硬币A |
| 3 | 1正-4反——0.08192 | 1正-4反——0.00567 | 最有可能的是硬币A |
| 4 | 3正2反——0.00512 | 3正2反——0.03087 | 最有可能的是硬币B |
| 5 | 2正-3反——0.02048 | 2正-3反——0.01323 | 最有可能的是硬币A |
此时根据更有可能的硬币计算新的 P A , P B P_A,P_B PA,PB:
P A = ( 2 + 1 + 2 ) / 15 = 0.33 P_A = (2+1+2) / 15 = 0.33 PA=(2+1+2)/15=0.33
P B = ( 3 + 3 ) / 10 = 0.6 P_B = (3+3) / 10 = 0.6 PB=(3+3)/10=0.6
至此,我们得到如下表:
| 初始化的 P A P_A PA | 估计出的 P A P_A PA | 真实的 P A P_A PA | 初始化的 P B P_B PB | 估计出的 P B P_B PB | 真实的 P B P_B PB |
|---|---|---|---|---|---|
| 0.2 | 0.33 | 0.4 | 0.7 | 0.6 | 0.5 |
其中,将上文中得到的 P A = 0.4 , P B = 0.5 P_A= 0.4,P_B = 0.5 PA=0.4,PB=0.5两个值称为 P A , P B P_A,P_B PA,PB的真实值。
由上表可以看出,我们估计的新的 P A , P B P_A,P_B PA,PB相比于它们的初始值更接近它们的真实值了,就这样重复迭代,不断接近真实值,这就是
EM算法的奇妙之处了。
三、EM算法
1、三硬币模型
假设有3枚硬币,分别记作 A , B , C A,B,C A,B,C,这些硬币正面出现的概率分别是 π , p , q \pi,p,q π,p,q,进行如下试验:
先掷硬币 A A A根据其结果选出硬币 B B B或者硬币 C C C,正面选硬币 B B B,反面选硬币 C C C;然后掷出选出的硬币,出现正面记为1,反面记为0;独立地重复 n n n次试验(这里 n n n取10),观测结果如下:
1101001101
假设只能观测到掷硬币的结果,不能观测掷硬币的过程,问如何估计三个硬币正面出现的概率,即三硬币模型的参数。
三硬币模型可写为:
p ( x ∣ θ ) = ∑ z p ( x , z ∣ θ ) = ∑ z p ( z ∣ θ ) p ( x ∣ z , θ ) = π p x ( 1 − p ) 1 − x + ( 1 − π ) q x ( 1 − q ) 1 − x p(x|\theta) = \sum_z p(x,z|\theta) = \sum_z p(z|\theta)p(x|z, \theta) \\ = \pi p^x(1-p)^{1-x}+ (1-\pi)q^x(1-q)^{1-x} p(x∣θ)=z∑p(x,z∣θ)=z∑p(z∣θ)p(x∣z,θ)=πpx(1−p)1−x+(1−π)qx(1−q)1−x
这里,随机变量 x x x是观测变量,表示一次试验观测的结果1或0;随机变量 z z z是隐变量,表示未观测到的掷硬币 A A A的结果; θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)是模型参数。
p ( A B ) = p ( A ) p ( B ∣ A ) p(AB) = p(A)p(B|A) p(AB)=p(A)p(B∣A)
下面将观测数据表示为 X = ( x 1 , x 2 , . . . , x n ) T X = (x_1,x_2,...,x_n)^T X=(x1,x2,...,xn)T,未观测数据表示为 Z = ( z 1 , z 2 , . . . , z n ) T Z = (z_1,z_2,...,z_n)^T Z=(z1,z2,...,zn)T,则观测数据的似然函数为:
p ( X ∣ θ ) = ∑ z p ( Z ∣ θ ) p ( X ∣ Z , θ ) p(X|\theta) = \sum_z p(Z|\theta)p(X|Z,\theta) p(X∣θ)=z∑p(Z∣θ)p(X∣Z,θ)
即:
p ( X ∣ θ ) = ∏ j = 1 n [ π p x j ( 1 − p ) 1 − x j + ( 1 − π ) q x j ( 1 − q ) 1 − x j ] p(X|\theta) = \prod_{j=1}^{n}[\pi p^{x_j}(1-p)^{1-x_j}+ (1-\pi)q^{x_j}(1-q)^{1-x_j}] p(X∣θ)=j=1∏n[πpxj(1−p)1−xj+(1−π)qxj(1−q)1−xj]
考虑求模型参数 θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)的极大似然估计,取对数似然:
θ M L E = a r g max θ l o g p ( X ∣ θ ) \theta_{MLE} = arg \max_\theta log \ p(X|\theta) θMLE=argθmaxlog p(X∣θ)
EM算法 通过迭代求 L ( θ ) = l o g p ( X ∣ θ ) \mathcal{L}(\theta) = log \ p(X|\theta) L(θ)=log p(X∣θ)的极大似然估计。每次迭代包含两步:
E步:求期望;M步:求极大化。
此问题的求解可见下文第三大点
2、EM算法
输入: 观测变量数据 X X X,隐变量数据 Z Z Z,联合分布 p ( X , Z ∣ θ ) p(X,Z|\theta) p(X,Z∣θ),条件分布 p ( Z ∣ X , θ ) p(Z|X,\theta) p(Z∣X,θ);
输出:模型参数 θ \theta θ
(1)选择参数的初值 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2)E步:记 θ ( i ) \theta^{(i)} θ(i)为第 i i i次迭代参数 θ \theta θ的估计值,在第 i + 1 i+1 i+1次迭代的E步,计算:
Q ( θ , θ ( i ) ) = E z [ l o g p ( X , Z ∣ θ ) ∣ X , θ ( i ) ] = ∑ z p ( X , Z ∣ θ ) p ( Z ∣ X , θ ( i ) ) Q(\theta,\theta^{(i)} )= E_z[log \ p(X,Z|\theta)|X,\theta^{(i)}] \\ =\sum_z p(X,Z|\theta)p(Z|X,\theta^{(i)}) Q(θ,θ(i))=Ez[log p(X,Z∣θ)∣X,θ(i)]=z∑p(X,Z∣θ)p(Z∣X,θ(i))
这里, p ( Z ∣ X , θ ( i ) ) p(Z|X,\theta^{(i)}) p(Z∣X,θ(i))表示在给定观测数据 X X X和当前的参数估计 θ ( i ) \theta^{(i)} θ(i)下隐变量数据 Z Z Z的条件概率分布;
(3)M步:求使 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)} ) Q(θ,θ(i))极大化的 θ \theta θ,确定第 i + 1 i+1 i+1次迭代的参数估计值 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)
θ ( i + 1 ) = a r g max θ Q ( θ , θ ( i ) ) \theta^{(i+1)} = arg \max_\theta Q(\theta,\theta^{(i)} ) θ(i+1)=argθmaxQ(θ,θ(i))
(4)重复第(2)步和第(3)步,直到收敛。
注:
- 函数 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)} ) Q(θ,θ(i))是
EM算法的核心,称为Q函数。- 参数的初值可以任意选择,但
EM算法对初值是敏感的- Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)} ) Q(θ,θ(i))中 θ \theta θ表示要极大化的参数, θ ( i ) \theta^{(i)} θ(i)表示当前估计值,每次迭代实际在求Q函数及其极大化
- M步求Q函数的极大化,得到 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),完成一次迭代
- 第(4)步给出停止迭代的条件,一般是对较小的正数 E 1 , E 2 \mathcal{E}_1,\mathcal{E}_2 E1,E2,若满足:
- ∣ ∣ θ ( i + 1 ) − θ ( i ) ∣ ∣ ⩽ E 1 , 或 ∣ ∣ Q ( θ ( i + 1 ) , θ ( i ) ) − Q ( θ ( i ) , θ ( i ) ) ∣ ∣ ⩽ E 2 ||\theta^{(i+1)}-\theta^{(i)}|| \leqslant \mathcal{E}_1,或 ||Q(\theta^{(i+1)},\theta^{(i)} )-Q(\theta^{(i)} ,\theta^{(i)} )|| \leqslant \mathcal{E}_2 ∣∣θ(i+1)−θ(i)∣∣⩽E1,或∣∣Q(θ(i+1),θ(i))−Q(θ(i),θ(i))∣∣⩽E2
- 则停止迭代。
3、 EM算法 公式推导
\quad\quad 上面我们给出了 EM算法 ,那么为什么 EM算法 能近似实现对观测数据的极大似然估计呢?下面通过近似求解观测数据的对数似然函数的极大化问题来导出 EM算法 。
由上面内容可以知道,极大化观测数据 X X X关于参数 θ \theta θ的对数似然函数,即极大化:
L ( θ ) = l o g p ( X ∣ θ ) = l o g ∑ z p ( X , Z ∣ θ ) = l o g ( ∑ z p ( X ∣ Z , θ ) p ( Z ∣ θ ) ) \mathcal{L}(\theta) = log\ p(X|\theta) = log \ \sum_z p(X,Z|\theta)= log \Big(\sum_z p(X|Z,\theta)p(Z|\theta)\Big) L(θ)=log p(X∣θ)=log z∑p(X,Z∣θ)=log(z∑p(X∣Z,θ)p(Z∣θ))
注意到:上式中有未观测数据并包含和的对数
事实上, EM算法 是通过迭代逐步近似极大化 L ( θ ) \mathcal{L}(\theta) L(θ)的。
假设在第 i i i次迭代后 θ \theta θ的估计值是 θ ( i ) \theta^{(i)} θ(i),我们希望新估计值 θ \theta θ能使 L ( θ ) \mathcal{L}(\theta) L(θ)增加,即 L ( θ ) > L ( θ ( i ) ) \mathcal{L}(\theta) > \mathcal{L}(\theta^{(i)}) L(θ)>L(θ(i)),并逐步达到极大值,为此考虑两者的差:
L ( θ ) − L ( θ ( i ) ) = l o g ( ∑ z p ( X ∣ Z , θ ) p ( Z ∣ θ ) ) − l o g p ( X ∣ θ ( i ) ) \mathcal{L}(\theta) - \mathcal{L}(\theta^{(i)}) = log \Big(\sum_z p(X|Z,\theta)p(Z|\theta)\Big) - log\ p(X|\theta^{(i)}) L(θ)−L(θ(i))=log(z∑p(X∣Z,θ)p(Z∣θ))−log p(X∣θ(i))
log函数为凹函数,利用 J e n s e n Jensen Jensen不等式(关于Jensen不等式可看下面第4点),即:函数的期望小于等于期望的函数
l o g ∑ j λ j y i ⩾ ∑ j λ j l o g y j log \sum_j \lambda_jy_i \geqslant \sum_j \lambda_j log\ y_j logj∑λjyi⩾j∑λjlog yj
其中 λ j ⩾ 0 , ∑ j λ j = 1 \lambda_j \geqslant 0, \sum_j \lambda_j = 1 λj⩾0,∑jλj=1
将两者差的式子前部分分子分母同时乘以 p ( X ∣ Z , θ ( i ) ) p(X|Z,\theta^{(i)}) p(X∣Z,θ(i)),在利用凹函数的Jensen不等式:
L ( θ ) − L ( θ ( i ) ) = l o g ( ∑ z p ( X ∣ Z , θ ( i ) ) p ( X ∣ Z , θ ) p ( Z ∣ θ ) p ( X ∣ Z , θ ( i ) ) ) − l o g p ( X ∣ θ ( i ) ) ⩾ ∑ z p ( Z ∣ X , θ ( i ) ) l o g p ( X ∣ Z , θ ) p ( Z ∣ θ ) p ( Z ∣ X , θ ( i ) ) − l o g p ( X ∣ θ ( i ) ) = ∑ z p ( Z ∣ X , θ ( i ) ) l o g p ( X ∣ Z , θ ) p ( Z ∣ θ ) p ( Z ∣ X , θ ( i ) ) p ( X ∣ θ ( i ) ) \mathcal{L}(\theta) - \mathcal{L}(\theta^{(i)}) = log \big(\sum_z p(X|Z,\theta^{(i)})\frac{p(X|Z,\theta)p(Z|\theta)}{p(X|Z,\theta^{(i)})}\big) - log\ p(X|\theta^{(i)}) \\ \geqslant \sum_z p(Z|X,\theta^{(i)})log\frac{p(X|Z,\theta)p(Z|\theta)}{p(Z|X,\theta^{(i)})} - log\ p(X|\theta^{(i)}) \\ = \sum_z p(Z|X,\theta^{(i)})log\frac{p(X|Z,\theta)p(Z|\theta)}{p(Z|X,\theta^{(i)})p(X|\theta^{(i)})} L(θ)−L(θ(i))=log(z∑p(X∣Z,θ(i))p(X∣Z,θ(i))p(X∣Z,θ)p(Z∣θ))−log p(X∣θ(i))⩾z∑p(Z∣X,θ(i))logp(Z∣X,θ(i))p(X∣Z,θ)p(Z∣θ)−log p(X∣θ(i))=z∑p(Z∣X,θ(i))logp(Z∣X,θ(i))p(X∣θ(i))p(X∣Z,θ)p(Z∣θ)
令:
B ( θ , θ ( i ) ) = L ( θ ( i ) ) + ∑ z p ( Z ∣ X , θ ( i ) ) l o g p ( X ∣ Z , θ ) p ( Z ∣ θ ) p ( Z ∣ X , θ ( i ) ) p ( X ∣ θ ( i ) ) B(\theta,\theta^{(i)}) = \mathcal{L}(\theta^{(i)})+\sum_z p(Z|X,\theta^{(i)})log\frac{p(X|Z,\theta)p(Z|\theta)}{p(Z|X,\theta^{(i)})p(X|\theta^{(i)})} B(θ,θ(i))=L(θ(i))+z∑p(Z∣X,θ(i))logp(Z∣X,θ(i))p(X∣θ(i))p(X∣Z,θ)p(Z∣θ)
则:
L ( θ ) ⩾ B ( θ , θ ( i ) ) \mathcal{L}(\theta) \geqslant B(\theta,\theta^{(i)}) L(θ)⩾B(θ,θ(i))
即函数 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))是 L ( θ ) \mathcal{L}(\theta) L(θ)的一个下届,因此任何使 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))增大的 θ \theta θ都会使 L ( θ ) \mathcal{L}(\theta) L(θ)的下届增大,也即使 L ( θ ) \mathcal{L}(\theta) L(θ)增大,为了使 L ( θ ) \mathcal{L}(\theta) L(θ)尽可能的大,自然选择使 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))达到最大的 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),即:
θ ( i + 1 ) = a r g max θ B ( θ , θ ( i ) ) \theta^{(i+1)} = arg \max_\theta B(\theta,\theta^{(i)}) θ(i+1)=argθmaxB(θ,θ(i))
现在求 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)的表达式,省去对 θ \theta θ的极大化而言的常数的项,有:
θ ( i + 1 ) = a r g max θ ( L ( θ ( i ) ) + ∑ z p ( Z ∣ X , θ ( i ) ) l o g p ( X ∣ Z , θ ) p ( Z ∣ θ ) p ( Z ∣ X , θ ( i ) ) p ( X ∣ θ ( i ) ) ) = a r g max θ ( ∑ z p ( Z ∣ X , θ ( i ) ) l o g ( p ( X ∣ Z , θ ) p ( Z ∣ θ ) ) ) = a r g max θ ( ∑ z p ( Z ∣ X , θ ( i ) ) l o g ( p ( X , Z ∣ θ ) ) = a r g max θ Q ( θ , θ ( i ) ) \theta^{(i+1)} = arg \max_\theta \big(\mathcal{L}(\theta^{(i)})+\sum_z p(Z|X,\theta^{(i)})log\frac{p(X|Z,\theta)p(Z|\theta)}{p(Z|X,\theta^{(i)})p(X|\theta^{(i)})} \big) \\ = arg \max_\theta \big(\sum_z p(Z|X,\theta^{(i)})log \ (p(X|Z,\theta)p(Z|\theta))\big) \\ = arg \max_\theta \big(\sum_z p(Z|X,\theta^{(i)})log \ (p(X,Z|\theta)\big) \\ = arg \max_\theta Q(\theta,\theta^{(i)}) θ(i+1)=argθmax(L(θ(i))+z∑p(Z∣X,θ(i))logp(Z∣X,θ(i))p(X∣θ(i))p(X∣Z,θ)p(Z∣θ))=argθmax(z∑p(Z∣X,θ(i))log (p(X∣Z,θ)p(Z∣θ)))=argθmax(z∑p(Z∣X,θ(i))log (p(X,Z∣θ))=argθmaxQ(θ,θ(i))
E M EM EM算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法。
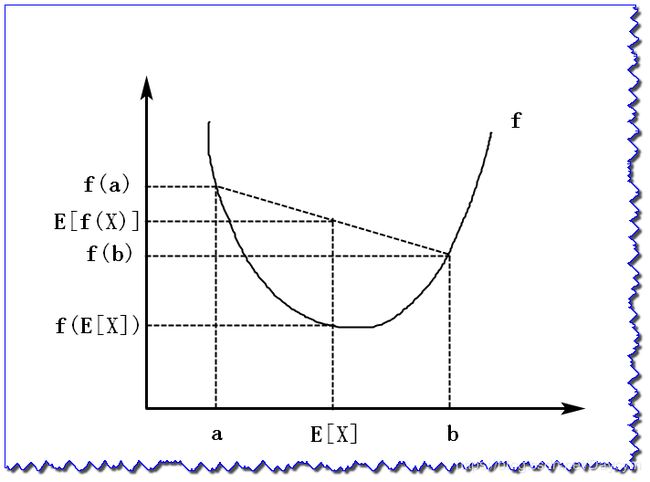
- 上图给出 E M EM EM算法的直观解释。图中上方曲线为 L ( θ ) \mathcal{L}(\theta) L(θ),下方曲线为 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)),图中在点 θ = θ ( i ) \theta = \theta^{(i)} θ=θ(i) 处时 L ( θ ) \mathcal{L}(\theta) L(θ) 并没用达到极大值,这时使 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))极大化,由于 L ( θ ) ⩾ B ( θ , θ ( i ) ) \mathcal{L}(\theta) \geqslant B(\theta,\theta^{(i)}) L(θ)⩾B(θ,θ(i)),所以 L ( θ ) \mathcal{L}(\theta) L(θ)在每次迭代中也是增加的。
- 在这个过程中, L ( θ ) \mathcal{L}(\theta) L(θ)不断增大,从图中可以看出
EM算法不能保证找到全局最优解。
使用迭代必须保证 p ( X ∣ θ ( i ) ) p(X|\theta^{(i)}) p(X∣θ(i))单调递增:
l o g p ( X ∣ θ ( i + 1 ) ) ⩾ l o g p ( X ∣ θ ( i ) ) log \ p(X|\theta^{(i+1)}) \geqslant log \ p(X|\theta^{(i)}) log p(X∣θ(i+1))⩾log p(X∣θ(i))
证明:
由:
p ( X ) = p ( X , Z ) p ( Z ∣ X ) p(X) = \frac{p(X,Z)}{p(Z|X)} p(X)=p(Z∣X)p(X,Z)
得到:
E [ l o g p ( X ∣ θ ) ] = E [ l o g p ( X , Z ∣ θ ) − l o g p ( Z ∣ X , θ ) ] E[log\ p(X|\theta)] = E[log \ p(X,Z|\theta)-log \ p(Z|X,\theta)] E[log p(X∣θ)]=E[log p(X,Z∣θ)−log p(Z∣X,θ)]
求期望,连续变量即求积分,离散变量即求和,上面我们用的都是求和,这个使用求积分,是为了让大家理解上面求和符号怎么来的。
上式左端:
= ∫ z l o g p ( X ∣ θ ) p ( Z ∣ X , θ ( i ) ) d z = l o g p ( X ∣ θ ) = \int_z log \ p(X|\theta)p(Z|X,\theta^{(i)})dz = log \ p(X|\theta) =∫zlog p(X∣θ)p(Z∣X,θ(i))dz=log p(X∣θ)
这个式子中, l o g p ( X ∣ θ ) log \ p(X|\theta) log p(X∣θ) 不包含 z z z,所以可以提出来;而 ∫ z p ( Z ∣ X , θ ( i ) ) d z = 1 \int_zp(Z|X,\theta^{(i)})dz = 1 ∫zp(Z∣X,θ(i))dz=1 ,也就是说在观测数据 X X X 下,属于某个分布 z i z_i zi 的概率,对属于每个分布的求积分(即一个数据属于每个分布的概率的和,自然等于1)
上式右端:
= ∫ z l o g p ( X , Z ∣ θ ) p ( Z ∣ X , θ ( i ) ) d z − ∫ z l o g p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( i ) d z = \int_z log \ p(X,Z|\theta)p(Z|X,\theta^{(i)})dz-\int_z log \ p(Z|X,\theta)p(Z|X,\theta^{(i)}dz =∫zlog p(X,Z∣θ)p(Z∣X,θ(i))dz−∫zlog p(Z∣X,θ)p(Z∣X,θ(i)dz
上式减号左边的式子与上面 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)中的式子一样,我们将其设为 Q ( θ , θ ( i ) ) Q(\theta, \theta^{(i)}) Q(θ,θ(i)),减号后面一项设为 H ( θ , θ ( i ) ) H(\theta, \theta^{(i)}) H(θ,θ(i))
那么对数似然函数(等式)可写为:
l o g p ( X ∣ θ ) = Q ( θ , θ ( i ) ) − H ( θ , θ ( i ) ) log \ p(X|\theta) = Q(\theta, \theta^{(i)}) - H(\theta, \theta^{(i)}) log p(X∣θ)=Q(θ,θ(i))−H(θ,θ(i))
因为求得是极大似然函数估计,那么 Q ( θ ( i + 1 ) , θ ( i ) ) ⩾ Q ( θ , θ ( i ) ) Q(\theta^{(i+1)}, \theta^{(i)}) \geqslant Q(\theta, \theta^{(i)}) Q(θ(i+1),θ(i))⩾Q(θ,θ(i));
-
假如对于所有的 θ \theta θ都有 H ( θ ( i ) , θ ( i ) ) ⩾ H ( θ , θ ( i ) ) H(\theta^{(i)}, \theta^{(i)}) \geqslant H(\theta, \theta^{(i)}) H(θ(i),θ(i))⩾H(θ,θ(i))
-
=> 那么 H ( θ ( i ) , θ ( i ) ) ⩾ H ( θ ( i + 1 ) , θ ( i ) ) H(\theta^{(i)}, \theta^{(i)}) \geqslant H(\theta^{(i+1)}, \theta^{(i)}) H(θ(i),θ(i))⩾H(θ(i+1),θ(i))
这样一来,对数似然函数就会逐渐增大。
那么我们又该如何证明对于所有的 θ \theta θ都有 H ( θ ( g ) , θ ( g ) ) ⩾ H ( θ , θ ( g ) ) H(\theta^{(g)}, \theta^{(g)}) \geqslant H(\theta, \theta^{(g)}) H(θ(g),θ(g))⩾H(θ,θ(g))
证明:
H ( θ ( i ) , θ ( i ) ) − H ( θ , θ ( i ) ) ⩾ 0 = ∫ z l o g p ( Z ∣ X , θ ( i ) ) p ( Z ∣ X , θ ( i ) ) d z − ∫ z l o g p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( i ) ) d z = ∫ z l o g ( p ( Z ∣ X , θ ( i ) ) p ( Z ∣ X , θ ) ) p ( Z ∣ X , θ ( i ) ) d z = − ∫ z l o g ( p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( i ) ) ) p ( Z ∣ X , θ ( i ) ) d z H(\theta^{(i)}, \theta^{(i)}) - H(\theta, \theta^{(i)}) \geqslant 0 \\ = \int_z log \ p(Z|X,\theta^{(i)})p(Z|X,\theta^{(i)})dz - \int_z log \ p(Z|X,\theta)p(Z|X,\theta^{(i)})dz \\ = \int_z log(\frac{p(Z|X,\theta^{(i)})}{p(Z|X,\theta)})p(Z|X,\theta^{(i)})dz \\ = - \int_z log(\frac{p(Z|X,\theta)}{p(Z|X,\theta^{(i)})})p(Z|X,\theta^{(i)})dz H(θ(i),θ(i))−H(θ,θ(i))⩾0=∫zlog p(Z∣X,θ(i))p(Z∣X,θ(i))dz−∫zlog p(Z∣X,θ)p(Z∣X,θ(i))dz=∫zlog(p(Z∣X,θ)p(Z∣X,θ(i)))p(Z∣X,θ(i))dz=−∫zlog(p(Z∣X,θ(i))p(Z∣X,θ))p(Z∣X,θ(i))dz
利用 J e n s e n Jensen Jensen不等式(函数的期望大于等于期望的函数):
⩾ − l o g ∫ z p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( i ) ) p ( Z ∣ X , θ ( i ) ) d z = 0 \geqslant -log \int_z\frac{p(Z|X,\theta)}{p(Z|X,\theta^{(i)})}p(Z|X,\theta^{(i)})dz = 0 ⩾−log∫zp(Z∣X,θ(i))p(Z∣X,θ)p(Z∣X,θ(i))dz=0
上式 l o g log log 中:
∫ z p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( i ) ) p ( Z ∣ X , θ ( i ) ) d z = 1 \int_z\frac{p(Z|X,\theta)}{p(Z|X,\theta^{(i)})}p(Z|X,\theta^{(i)})dz=1 ∫zp(Z∣X,θ(i))p(Z∣X,θ)p(Z∣X,θ(i))dz=1
消去 p ( Z ∣ X , θ ( i ) ) p(Z|X,\theta^{(i)}) p(Z∣X,θ(i))为:
∫ z p ( Z ∣ X , θ ) d z = 1 \int_zp(Z|X,\theta)dz = 1 ∫zp(Z∣X,θ)dz=1
4、Jensen不等式
设 f f f 是定义域为实数的函数:
- 如果对于所有的实数 x x x , f ( x ) f(x) f(x) 的二次导数 f ′ ′ ( x ) ⩾ 0 f''(x) \geqslant 0 f′′(x)⩾0,那么 f f f 是凸函数;
- 当 x x x 是向量时,如果其
hessian矩阵H H H 是半正定的( H ⩾ 0 H \geqslant 0 H⩾0),那么 f f f 是凸函数; - 如果 f ′ ′ ( x ) ⩾ 0 f''(x) \geqslant 0 f′′(x)⩾0 或者 H ⩾ 0 H \geqslant 0 H⩾0,那么 f f f 是严格凸函数。
Jensen不等式 表述如下:
如果 f f f 是凸函数, X X X 是随机变量,那么:
E [ f ( X ) ] ⩾ f ( E [ X ] ) E[f(X)] \geqslant f(E[X]) E[f(X)]⩾f(E[X])
也即:函数的期望大于等于期望的函数
- 特别地,如果 f f f 是严格凸函数,当且仅当 P ( X = E [ X ] ) = 1 P(X = E[X]) = 1 P(X=E[X])=1,即 X X X 是常量时,上式取等号
当 f f f 是凹函数,不等号方向反向即可,即 E [ f ( x ) ] ⩽ f ( E [ X ] ) E[f(x)] \leqslant f(E[X]) E[f(x)]⩽f(E[X])
四、三硬币模型 EM算法 求解
在前面我们提到了三硬币模型,这里我们给出具体的计算过程,以及Python代码实现
首先前面我们得到了:
对数似然:
θ M L E = a r g max θ l o g p ( X ∣ θ ) \theta_{MLE} = arg \max_\theta log \ p(X|\theta) θMLE=argθmaxlog p(X∣θ)
EM算法 是通过迭代求 L ( θ ) = l o g p ( X ∣ θ ) \mathcal{L}(\theta) = log \ p(X|\theta) L(θ)=log p(X∣θ)的极大似然估计。每次迭代包含两步:
E步:求期望;M步:求极大化。
1、使用 EM算法 求解
- 符号标记:
- x j x_j xj 为第 j j j 次实验的观测,只有两个取值0/1;
- Z Z Z 为隐变量,表示抛硬币 A A A 出现的结果,该变量只有两个取值 0/1;
- z j z_j zj 为第 j j j 次实验时,抛硬币 A A A 出现的结果,同样的, z j = 1 z_j=1 zj=1 表示硬币 A A A 抛出正面;
- θ \theta θ 表示模型参数集合 π , p , q \pi,p,q π,p,q;
- θ ( i ) \theta^{(i)} θ(i) 为第 i i i 次迭代时, π , p , q \pi,p,q π,p,q 的估计值。
- E步:
完全数据的对数似然函数为:
l o g ( p ( X , Z ∣ θ ) ) = l o g ( ∏ j = 1 n p ( x j , z j ∣ θ ) ) = ∑ j = 1 n l o g ( p ( x j , z j ∣ θ ) ) log(p(X,Z|\theta)) = log (\prod_{j=1}^n p(x_j,z_j|\theta)) \\ = \sum_{j=1}^nlog(p(x_j,z_j|\theta)) log(p(X,Z∣θ))=log(j=1∏np(xj,zj∣θ))=j=1∑nlog(p(xj,zj∣θ))
期望为:
E Z ∣ X , θ ( i ) [ l o g ( p ( X , Z ∣ θ ) ) ] = ∑ j = 1 n ∑ z j [ p ( z j ∣ x j , θ ( i ) ) l o g ( p ( x j , z j ∣ θ ) ) ] E_{Z|X,\theta^{(i)}}[log(p(X,Z|\theta)) ]=\sum_{j=1}^n\sum_{z_j}[p(z_j|x_j,\theta^{(i)})log(p(x_j,z_j|\theta))] EZ∣X,θ(i)[log(p(X,Z∣θ))]=j=1∑nzj∑[p(zj∣xj,θ(i))log(p(xj,zj∣θ))]
= ∑ j = 1 n [ [ p ( z j = 1 ∣ x j , θ ( i ) ) l o g ( p ( x j , z j = 1 ∣ θ ) ) ] + [ p ( z j = 0 ∣ x j , θ ( i ) ) l o g ( p ( x j , z j = 0 ∣ θ ) ) ] ] =\sum_{j=1}^n\Big[[p(z_j=1|x_j,\theta^{(i)})log(p(x_j,z_j=1|\theta))]+[p(z_j=0|x_j,\theta^{(i)})log(p(x_j,z_j=0|\theta))]\Big] =j=1∑n[[p(zj=1∣xj,θ(i))log(p(xj,zj=1∣θ))]+[p(zj=0∣xj,θ(i))log(p(xj,zj=0∣θ))]]
上式中 z j z_j zj 只有两个取值;
对于后验概率 p ( z j ∣ x j ; θ ( i ) ) p(z_j|x_j;\theta^{(i)}) p(zj∣xj;θ(i)),这里先求 z j = 1 z_j=1 zj=1 的情况, z j = 0 z_j=0 zj=0 的情况类似:
μ j ( i + 1 ) = p ( z j = 1 ∣ x j ; θ ( i ) ) \mu_j^{(i+1)} = p(z_j=1|x_j;\theta^{(i)}) μj(i+1)=p(zj=1∣xj;θ(i))
= p ( x j ∣ z j = 1 ) p ( z j = 1 ) p ( x j ) = \frac{p(x_j|z_j=1)p(z_j=1)}{ p(x_j)} =p(xj)p(xj∣zj=1)p(zj=1)上式用到贝叶斯公式:
p ( A ∣ B ) = p ( B ∣ A ) p ( A ) p ( B ) p(A|B) = \frac{p(B|A)p(A)}{p(B)} p(A∣B)=p(B)p(B∣A)p(A)又:
p ( x j ) = ∑ z j p ( x j , z j ) p(x_j) = \sum_{z_j}p(x_j,z_j) p(xj)=zj∑p(xj,zj)所以上式:
= p ( x j ∣ z j = 1 ) p ( z j = 1 ) ∑ z j p ( x j , z j ) = \frac{p(x_j|z_j=1)p(z_j=1)}{ \sum_{z_j}p(x_j,z_j)} =∑zjp(xj,zj)p(xj∣zj=1)p(zj=1)
= p ( x j ∣ z j = 1 ) p ( z j = 1 ) p ( x j , z j = 1 ) + p ( x j , z j = 0 ) = \frac{p(x_j|z_j=1)p(z_j=1)}{ p(x_j,z_j=1)+p(x_j,z_j=0)} =p(xj,zj=1)+p(xj,zj=0)p(xj∣zj=1)p(zj=1)
μ j ( i + 1 ) = ( p ( i ) ) x j ( 1 − p ( i ) ) ( 1 − x j ) × π ( i ) ( p ( i ) ) x j ( 1 − p ( i ) ) ( 1 − x j ) × π ( i ) + ( q ( i ) ) x j ( 1 − q ( i ) ) ( 1 − x j ) × ( 1 − π ( i ) ) \mu_j^{(i+1)}=\frac{(p^{(i)})^{x_j}(1-p^{(i)})^{(1-x_j)} \times \pi^{(i)}}{(p^{(i)})^{x_j}(1-p^{(i)})^{(1-x_j)} \times \pi^{(i)}+(q^{(i)})^{x_j}(1-q^{(i)})^{(1-x_j)} \times (1-\pi^{(i)})} μj(i+1)=(p(i))xj(1−p(i))(1−xj)×π(i)+(q(i))xj(1−q(i))(1−xj)×(1−π(i))(p(i))xj(1−p(i))(1−xj)×π(i)其实,上式也就是在模型参数 θ ( i ) \theta^{(i)} θ(i) 下,观测数据 x j x_j xj 来自硬币 B B B 的概率,那么来自 硬币 C C C 的概率可以表示为:
1 − μ j ( i + 1 ) 1- \mu_j^{(i+1)} 1−μj(i+1)对于联合概率 p ( x j , z j ∣ θ ) p(x_j,z_j|\theta) p(xj,zj∣θ):
p ( x j , z j = 1 ∣ θ ) = p ( x j ∣ z j = 1 , θ ) p ( z j = 1 ∣ θ ) p(x_j,z_j=1|\theta) = p(x_j|z_j=1,\theta)p(z_j=1|\theta) p(xj,zj=1∣θ)=p(xj∣zj=1,θ)p(zj=1∣θ)
= π p x j ( 1 − p ) 1 − x j =\pi p^{x_j}(1-p)^{1-x_j} =πpxj(1−p)1−xj上式用到:
p ( B A ) = p ( A B ) = p ( B ∣ A ) p ( A ) p(BA) =p(AB)= p(B|A)p(A) p(BA)=p(AB)=p(B∣A)p(A)同样:
p ( x j , z j = 0 ∣ θ ) = p ( x j ∣ z j = 1 , θ ) p ( z j = 0 ∣ θ ) p(x_j,z_j=0|\theta) = p(x_j|z_j=1,\theta)p(z_j=0|\theta) p(xj,zj=0∣θ)=p(xj∣zj=1,θ)p(zj=0∣θ)
= ( 1 − π ) q x j ( 1 − q ) 1 − x j =(1-\pi) q^{x_j}(1-q)^{1-x_j} =(1−π)qxj(1−q)1−xj
所以最终结果为:
E Z ∣ X , θ ( i ) [ l o g ( p ( X , Z ∣ θ ) ) ] E_{Z|X,\theta^{(i)}}[log(p(X,Z|\theta)) ] EZ∣X,θ(i)[log(p(X,Z∣θ))]
= ∑ j = 1 n [ [ p ( z j = 1 ∣ x j , θ ( i ) ) l o g ( p ( x j , z j = 1 ∣ θ ) ) ] + [ p ( z j = 0 ∣ x j , θ ( i ) ) l o g ( p ( x j , z j = 0 ∣ θ ) ) ] ] =\sum_{j=1}^n\Big[[p(z_j=1|x_j,\theta^{(i)})log(p(x_j,z_j=1|\theta))]+[p(z_j=0|x_j,\theta^{(i)})log(p(x_j,z_j=0|\theta))]\Big] =j=1∑n[[p(zj=1∣xj,θ(i))log(p(xj,zj=1∣θ))]+[p(zj=0∣xj,θ(i))log(p(xj,zj=0∣θ))]]
= ∑ j = 1 n [ [ μ j ( i + 1 ) × l o g ( π p x j ( 1 − p ) 1 − x j ] + [ ( 1 − μ j ( i + 1 ) ) × l o g ( ( 1 − π ) q x j ( 1 − q ) 1 − x j ] ] =\sum_{j=1}^n\Big[[\mu_j^{(i+1)} \times log(\pi p^{x_j}(1-p)^{1-x_j}]+[(1- \mu_j^{(i+1)})\times log((1-\pi) q^{x_j}(1-q)^{1-x_j}]\Big] =j=1∑n[[μj(i+1)×log(πpxj(1−p)1−xj]+[(1−μj(i+1))×log((1−π)qxj(1−q)1−xj]]
令:
f = ∑ j = 1 n [ [ μ j ( i + 1 ) × l o g ( π p x j ( 1 − p ) 1 − x j ] + [ ( 1 − μ j ( i + 1 ) ) × l o g ( ( 1 − π ) q x j ( 1 − q ) 1 − x j ] ] f = \sum_{j=1}^n\Big[[\mu_j^{(i+1)} \times log(\pi p^{x_j}(1-p)^{1-x_j}]+[(1- \mu_j^{(i+1)})\times log((1-\pi) q^{x_j}(1-q)^{1-x_j}]\Big] f=j=1∑n[[μj(i+1)×log(πpxj(1−p)1−xj]+[(1−μj(i+1))×log((1−π)qxj(1−q)1−xj]]
- M步:
对上面的期望最终表达式求偏导,并令偏导数为0,来估计每个参数:
- (1)估计参数 π \pi π
对 π \pi π 求偏导,其中 μ ( i + 1 ) \mu^{(i+1)} μ(i+1) 为常数:
∂ f ∂ π = ∑ j = 1 n { μ j ( i + 1 ) × 1 π − ( 1 − μ j ( i + 1 ) ) × 1 1 − π } \frac{\partial f}{\partial \pi} = \sum_{j=1}^n \Big\{\mu_j^{(i+1)} \times \frac{1}{\pi} - (1- \mu_j^{(i+1)}) \times \frac{1}{1 - \pi}\Big\} ∂π∂f=j=1∑n{μj(i+1)×π1−(1−μj(i+1))×1−π1}
= ∑ j = 1 n { π − μ j ( i + 1 ) π ( 1 − π ) } =\sum_{j=1}^n\Big\{\frac{\pi - \mu_j^{(i+1)}}{\pi(1-\pi)}\Big\} =j=1∑n{π(1−π)π−μj(i+1)}
= n π − ∑ j = 1 n μ j ( i + 1 ) π ( 1 − π ) = 0 = \frac{n\pi - \sum_{j=1}^n \mu_j^{(i+1)}}{\pi(1-\pi)}=0 =π(1−π)nπ−∑j=1nμj(i+1)=0
求得 π \pi π 的估计为:
π = 1 n ∑ j = 1 n μ j ( i + 1 ) \pi = \frac{1}{n} \sum_{j=1}^n \mu_j^{(i+1)} π=n1j=1∑nμj(i+1)
- (2)估计参数 p p p
对 p p p 求偏导:
∂ f ∂ p = ∑ j = 1 n μ j ( i + 1 ) × π { x j p x j − 1 ( 1 − p ) 1 − x j + p x j [ − ( 1 − x j ) ( 1 − p ) − x j ] } π p x j ( 1 − p ) 1 − x j \frac{\partial f}{\partial p} =\sum_{j=1}^n\mu_j^{(i+1)} \times \frac{\pi\Big\{x_jp^{x_j-1}(1-p)^{1-x_j} + p^{x_j}[-(1-x_j)(1-p)^{-x_j}]\Big\}}{\pi p^{x_j}(1-p)^{1-x_j}} ∂p∂f=j=1∑nμj(i+1)×πpxj(1−p)1−xjπ{xjpxj−1(1−p)1−xj+pxj[−(1−xj)(1−p)−xj]}
= ∑ j = 1 n μ j ( i + 1 ) × { x j p − 1 + [ − ( 1 − x j ) ( 1 − p ) − 1 ] } =\sum_{j=1}^n\mu_j^{(i+1)} \times \Big\{x_j p^{-1}+[-(1-x_j)(1-p)^{-1}]\Big\} =j=1∑nμj(i+1)×{xjp−1+[−(1−xj)(1−p)−1]}
= ∑ j = 1 n μ j ( i + 1 ) × { x j p − 1 − x j 1 − p } =\sum_{j=1}^n\mu_j^{(i+1)} \times \Big\{\frac{x_j}{p}-\frac{1-x_j}{1-p}\Big\} =j=1∑nμj(i+1)×{pxj−1−p1−xj}
= ∑ j = 1 n μ j ( i + 1 ) × { x j ( 1 − p ) + p ( x j − 1 ) p ( 1 − p ) } =\sum_{j=1}^n\mu_j^{(i+1)} \times \Big\{\frac{x_j(1-p)+p(x_j-1)}{p(1-p)}\Big\} =j=1∑nμj(i+1)×{p(1−p)xj(1−p)+p(xj−1)}
= ∑ j = 1 n μ j ( i + 1 ) × { x j − p p ( 1 − p ) } = 0 =\sum_{j=1}^n\mu_j^{(i+1)} \times \Big\{\frac{x_j-p}{p(1-p)}\Big\} = 0 =j=1∑nμj(i+1)×{p(1−p)xj−p}=0
求得 p p p 的估计为:
p = ∑ j = 1 n μ j ( i + 1 ) x j ∑ j = 1 n μ j ( i + 1 ) p = \frac{\sum_{j=1}^n \mu_j^{(i+1)}x_j}{\sum_{j=1}^n \mu_j^{(i+1)}} p=∑j=1nμj(i+1)∑j=1nμj(i+1)xj
- (3)估计参数 q q q
对 q q q 求偏导:
∂ f ∂ q = ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) × ( 1 − π ) { x j q x j − 1 ( 1 − q ) 1 − x j + q x j [ − ( 1 − x j ) ( 1 − q ) − x j ] } ( 1 − π ) q x j ( 1 − q ) 1 − x j \frac{\partial f}{\partial q} = \sum_{j=1}^n(1-\mu_j^{(i+1)})\times\frac{(1-\pi)\Big\{x_jq^{x_j-1}(1-q)^{1-x_j}+q^{x_j}[-(1-x_j)(1-q)^{-x_j}]\Big\}}{(1-\pi)q^{x_j}(1-q)^{1-x_j}} ∂q∂f=j=1∑n(1−μj(i+1))×(1−π)qxj(1−q)1−xj(1−π){xjqxj−1(1−q)1−xj+qxj[−(1−xj)(1−q)−xj]}
= ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) × [ x j q − 1 + ( x j − 1 ) ( 1 − q ) − 1 ] =\sum_{j=1}^n(1-\mu_j^{(i+1)})\times \Big[x_jq^{-1}+(x_j-1)(1-q)^{-1}\Big] =j=1∑n(1−μj(i+1))×[xjq−1+(xj−1)(1−q)−1]
= ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) × [ x j q + x j − 1 1 − q ] =\sum_{j=1}^n(1-\mu_j^{(i+1)})\times\Big[\frac{x_j}{q}+\frac{x_j-1}{1-q}\Big] =j=1∑n(1−μj(i+1))×[qxj+1−qxj−1]
= ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) × x j − q q ( 1 − q ) = 0 =\sum_{j=1}^n(1-\mu_j^{(i+1)})\times \frac{x_j-q}{q(1-q)}=0 =j=1∑n(1−μj(i+1))×q(1−q)xj−q=0
求得 q q q 的估计为:
q = ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) x j ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) q = \frac{\sum_{j=1}^n (1-\mu_j^{(i+1)})x_j}{\sum_{j=1}^n (1-\mu_j^{(i+1)})} q=∑j=1n(1−μj(i+1))∑j=1n(1−μj(i+1))xj
2、具体数字计算
- 假设模型参数的初始值为:
π ( 0 ) = 0.5 , p ( 0 ) = 0.5 , q ( 0 ) = 0.5 \pi^{(0)}=0.5,p^{(0)}=0.5,q^{(0)}=0.5 π(0)=0.5,p(0)=0.5,q(0)=0.5
- 由 μ j ( i + 1 ) \mu_j^{(i+1)} μj(i+1)公式,对 x j = 1 x_j=1 xj=1 与 x j = 0 x_j=0 xj=0 均有:
μ j ( 1 ) = 0.5 \mu_j^{(1)} = 0.5 μj(1)=0.5
- 根据参数迭代公式,可得:
π ( 1 ) = 0.5 , p ( 1 ) = 0.6 , q ( 1 ) = 0.6 \pi^{(1)}=0.5,p^{(1)}=0.6,q^{(1)}=0.6 π(1)=0.5,p(1)=0.6,q(1)=0.6
- 在根据更新后的参数,更新 μ j ( 2 ) \mu_j^{(2)} μj(2):
μ j ( 2 ) = 0.5 \mu_j^{(2)}=0.5 μj(2)=0.5
- 继续迭代:
π ( 2 ) = 0.5 , p ( 2 ) = 0.6 , q ( 2 ) = 0.6 \pi^{(2)}=0.5,p^{(2)}=0.6,q^{(2)}=0.6 π(2)=0.5,p(2)=0.6,q(2)=0.6
此时,参数不发生改变,所以得到模型参数的极大似然估计为:
π ^ = 0.5 , p ^ = 0.6 , q ^ = 0.6 \hat{\pi}=0.5,\hat{p}=0.6,\hat{q}=0.6 π^=0.5,p^=0.6,q^=0.6
3、Python代码实现
代码可见:01_三硬币模型EM算法求解
运行结果:
init prob:0.5, 0.5, 0.5
1/10 pro_a:0.500, pro_b:0.600, pro_c:0.600
2/10 pro_a:0.500, pro_b:0.600, pro_c:0.600
init prob:0.4, 0.6, 0.7
1/10 pro_a:0.406, pro_b:0.537, pro_c:0.643
2/10 pro_a:0.406, pro_b:0.537, pro_c:0.643
由运行结果可见:
- 不同初始化值会得到不同的参数估计值,也就是说
EM算法与初值的选择有关,选择不同的初值可能得到不同的参数估计值。
五、EM算法 在高斯混合模型中的应用
1、单个高斯分布
\quad\quad 如上左图,假如我们有一些数据,这些数据来自同一个高斯分布(独立同分布),那么我们如何根据这些数据估计出这个高斯分布的参数呢?我们知道只要知道高斯分布的参数 θ = { μ , σ 2 } \theta=\{\mu,\sigma^2\} θ={μ,σ2}就能确定此高斯分布。
\quad\quad 前面第一大点:最大似然估计中第4点的例子解释,便可以根据观测数据来计算出未知的模型参数,从而确定数据的分布。
2、高斯混合模型
\quad\quad 如上右图中的红色曲线,是一个高斯混合模型,此处只画了两个高斯分布,可以是多个高斯分布。
\quad\quad 如果我们知道每一个数据属于哪一个高斯分布,就会很容易求解,但是我们不可能都知道的,这时随便一个数据点,我们应该如何判断它是哪个高斯分布产生的呢?
假定高斯混合模型 (Gaussian Mixture Model, GMM)是指由多个高斯模型 线性叠加 混合而成,那么概率密度函数可以表述如下:
这里我们引入 α k \alpha_k αk表示属于第 k k k个高斯分布的权重,并满足 ∑ k = 1 K α k = 1 \sum_{k=1}^{K} \alpha_k = 1 ∑k=1Kαk=1
这样我们可以得到:
p ( X ∣ θ ) = ∑ k = 1 K α k N ( μ k , σ k 2 ) ∑ k = 1 K α k = 1 p(X|\theta) = \sum_{k=1}^{K} \alpha_k \mathcal{N}(\mu_k, \sigma^2_k) \\ \sum_{k=1}^{K} \alpha_k= 1 p(X∣θ)=k=1∑KαkN(μk,σk2)k=1∑Kαk=1
其中 N ( μ k , σ k 2 ) \mathcal{N}(\mu_k, \sigma^2_k) N(μk,σk2)是高斯分布, α k \alpha_k αk是系数
给出定义:
高斯混合模型是指具有如下形式的概率分布模型:
p ( x ∣ θ ) = ∑ k = 1 K α k ϕ ( x ∣ θ k ) p(x|\theta) = \sum_{k=1}^{K}\alpha_k \phi(x|\theta_k) p(x∣θ)=k=1∑Kαkϕ(x∣θk)
其中, α k \alpha_k αk是系数, α k ⩾ 0 ∑ k = 1 K α k = 1 \alpha_k\geqslant 0 \sum_{k=1}^{K} \alpha_k= 1 αk⩾0∑k=1Kαk=1; ϕ ( x ∣ θ k ) \phi(x|\theta_k) ϕ(x∣θk)是高斯分布密度, θ k = ( μ k , σ k 2 ) \theta_k = (\mu_k, \sigma^2_k) θk=(μk,σk2),
ϕ ( x ∣ θ k ) = 1 2 π σ k e x p ( − ( x − μ k ) 2 2 σ k 2 ) \phi(x|\theta_k) = \frac{1}{\sqrt{2\pi}\sigma_k}exp(-\frac{(x - \mu_k)^2}{2\sigma_k^2}) ϕ(x∣θk)=2πσk1exp(−2σk2(x−μk)2)
称为第 k k k个分模型。
3、高斯混合模型参数估计的 E M EM EM算法
假设观测数据 x 1 , x 2 , . . . , x N x_1,x_2,...,x_N x1,x2,...,xN由高斯混合模型生成:
p ( x ∣ θ ) = ∑ k = 1 K α k ϕ ( x ∣ θ k ) p(x|\theta) = \sum_{k=1}^K\alpha_k \phi(x|\theta_k) p(x∣θ)=k=1∑Kαkϕ(x∣θk)
其中, θ = ( α 1 , α 2 , . . , α k ; θ 1 , θ 2 , . . , θ k ) \theta = (\alpha_1,\alpha_2,..,\alpha_k;\theta_1,\theta_2,..,\theta_k) θ=(α1,α2,..,αk;θ1,θ2,..,θk),我们用 E M EM EM算法估计高斯混合模型的参数 θ \theta θ.
(1)明确隐变量,写出完全数据的对数似然函数
我们设想数据是这样产生的:
- 首先依概率 α k \alpha_k αk 选择第 k k k 个高斯分布模型 ϕ ( x ∣ θ k ) \phi(x|\theta_k) ϕ(x∣θk);
- 然后依第 k k k 个分模型的概率分布 ϕ ( x ∣ θ k ) \phi(x|\theta_k) ϕ(x∣θk) 生成观测数据 x j x_j xj,此时观测数据 x j x_j xj 是已知的;
- 反映观测数据 x j x_j xj来自第 k k k个分模型的数据是未知的, k = 1 , 2 , . . . , K k = 1,2,...,K k=1,2,...,K,以隐变量 γ j k \gamma_{jk} γjk 表示,其定义如下:
γ j k = { 1 , 第 j 个 观 测 来 自 第 k 个 分 模 型 0 , 否 则 \gamma_{jk}=\begin{cases} 1,\quad 第j个观测来自第k个分模型 \\ 0, \quad 否则 \\ \end{cases} γjk={1,第j个观测来自第k个分模型0,否则
j = 1 , 2 , . . . , N ; k = 1 , 2 , . . . , K j = 1,2,...,N; k = 1,2,...,K j=1,2,...,N;k=1,2,...,K
有了观测数据 x j x_j xj及未观测数据 γ j k \gamma_{jk} γjk,那么完全数据是: ( x j , γ j 1 , γ j 2 , . . . , γ j K ) , j = 1 , 2 , . . . , N (x_j,\gamma_{j1},\gamma_{j2},...,\gamma_{jK}), j = 1,2,...,N (xj,γj1,γj2,...,γjK),j=1,2,...,N
于是,可以写出完全数据的似然函数:
p ( x , γ ∣ θ ) = ∏ j = 1 N p ( x j , γ j 1 , γ j 2 , . . . , γ j K ∣ θ ) p(x,\gamma|\theta) = \prod_{j=1}^Np(x_j,\gamma_{j1},\gamma_{j2},...,\gamma_{jK}|\theta) p(x,γ∣θ)=j=1∏Np(xj,γj1,γj2,...,γjK∣θ)
= ∏ k = 1 K ∏ j = 1 N [ α k ϕ ( x j ∣ θ k ) ] γ j k = \prod_{k=1}^K\prod_{j=1}^N[\alpha_k \phi(x_j|\theta_k)]^{\gamma_{jk}} =k=1∏Kj=1∏N