【Tensorflow】Tensorflow构建VGG实现17种花数据分类

前言

【Tensorflow】Tensorflow构建LeNet实现手写数字识别

  前面我们动手构建了LeNet 网络结构，并实现手写数字的识别，本篇和上篇基本类似，我们构建 VGG网络结构来对17中花的数据集进行分类。

本篇代码可见：Github

一、数据的获取

  17中花数据分类，是VGG网络初赛时候的数据集，现在网上没有下载；现在唯一一份数据集在tflearn这个框架中默认自带

tflearn安装：pip install tflearn

from tflearn.datasets import oxflower17

# 读取数据
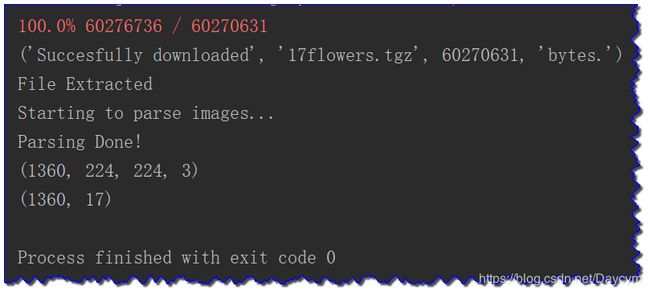
X, Y = oxflower17.load_data(dirname="17flowers", one_hot=True)
print(X.shape)  # sample_number,224,224,3
print(Y.shape)  # sample_number,17

二、相关参数和超参数的设置

# 相关的参数、超参数的设置
# 学习率，一般学习率设置的比较小
learn_rate = 0.1
# 每次迭代的训练样本数量
batch_size = 32
# 训练迭代次数(每个迭代次数中必须训练完一次所有的数据集)
train_epoch = 10000  # 如果只是想看程序是否可以运行以及可视化结果，可以设置为20
# 样本数量
total_sample_number = X.shape[0]

这里我们使用固定的学习率

三、模型的构建

1、输入输出数据的占位符

# 1. 设置数据输入的占位符
x = tf.placeholder(tf.float32, shape=[None, 224, 224, 3], name='x')
y = tf.placeholder(tf.float32, shape=[None, 17], name='y')


# 返回一个对应的变量，用于对w和b的更新
def get_variable(name, shape=None, dtype=tf.float32, initializer=tf.random_normal_initializer(mean=0, stddev=0.1)):
    return tf.get_variable(name, shape, dtype, initializer)

2、VGG网络结构构建

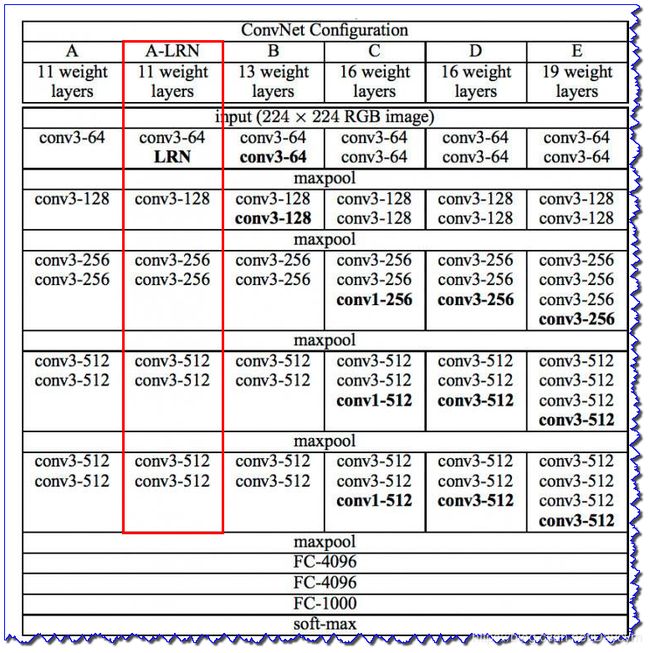
这里我们选择 A-LRN 网络结构

# 网络的构建
def vgg_network(x, y):
    net1_kernel_size = 8
    net3_kernel_size = 16
    net5_kernal_size_1 = 32
    net5_kernal_size_2 = 32
    net7_kernal_size_1 = 64
    net7_kernal_size_2 = 64
    net9_kernal_size_1 = 64
    net9_kernal_size_2 = 64
    net11_unit_size = 1000
    net12_unit_size = 1000
    net13_unit_size = 17

    # cov3-64 lrn
    with tf.variable_scope('net1'):
        net = tf.nn.conv2d(x, filter=get_variable('w', [3, 3, 3, net1_kernel_size]), strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b', [net1_kernel_size]))
        net = tf.nn.relu(net)
        # lrn(input, depth_radius=5, bias=1, alpha=1, beta=0.5, name=None)
        # 做一个局部响应归一化，是对卷积核的输出值做归一化
        # depth_radius ==> 对应ppt公式上的n，bias => 对应ppt公式上的k, alpha => 对应ppt公式上的α, beta=>对应ppt公式上的β
        net = tf.nn.lrn(net)
    # maxpool
    with tf.variable_scope('net2'):
        net = tf.nn.max_pool(net, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
    # conv3-128
    with tf.variable_scope('net3'):
        net = tf.nn.conv2d(net, filter=get_variable('w', [3, 3, net1_kernel_size, net3_kernel_size]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b', [net3_kernel_size]))
        net = tf.nn.relu(net)
    # maxpool
    with tf.variable_scope('net4'):
        net = tf.nn.max_pool(net, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
    # conv3-256 conv3-256
    with tf.variable_scope('net5'):
        net = tf.nn.conv2d(net, filter=get_variable('w1', [3, 3, net3_kernel_size, net5_kernal_size_1]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b1', [net5_kernal_size_1]))
        net = tf.nn.relu(net)

        net = tf.nn.conv2d(net, filter=get_variable('w2', [3, 3, net5_kernal_size_1, net5_kernal_size_2]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b2', [net5_kernal_size_2]))
        net = tf.nn.relu(net)
    # maxpool
    with tf.variable_scope('net6'):
        net = tf.nn.max_pool(net, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
    # conv3-512 conv3-512
    with tf.variable_scope('net7'):
        net = tf.nn.conv2d(net, filter=get_variable('w1', [3, 3, net5_kernal_size_2, net7_kernal_size_1]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b1', [net7_kernal_size_1]))
        net = tf.nn.relu(net)

        net = tf.nn.conv2d(net, filter=get_variable('w2', [3, 3, net7_kernal_size_1, net7_kernal_size_2]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b2', [net7_kernal_size_2]))
        net = tf.nn.relu(net)
    # maxpool
    with tf.variable_scope('net8'):
        net = tf.nn.max_pool(net, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
    # conv3-512 conv3-512
    with tf.variable_scope('net9'):
        net = tf.nn.conv2d(net, filter=get_variable('w1', [3, 3, net7_kernal_size_2, net9_kernal_size_1]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b1', [net9_kernal_size_1]))
        net = tf.nn.relu(net)

        net = tf.nn.conv2d(net, filter=get_variable('w2', [3, 3, net9_kernal_size_1, net9_kernal_size_2]),
                           strides=[1, 1, 1, 1],
                           padding='SAME')
        net = tf.nn.bias_add(net, get_variable('b2', [net9_kernal_size_2]))
        net = tf.nn.relu(net)
    # maxpool
    with tf.variable_scope('net10'):
        net = tf.nn.max_pool(net, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
    # fc
    with tf.variable_scope('net11'):
        # 将四维的数据转换为两维的数据
        shape = net.get_shape()
        feature_number = shape[1] * shape[2] * shape[3]
        net = tf.reshape(net, shape=[-1, feature_number])
        # 全连接
        net = tf.add(tf.matmul(net, get_variable('w', [feature_number, net11_unit_size])),
                     get_variable('b', [net11_unit_size]))
        net = tf.nn.relu(net)
    # fc
    with tf.variable_scope('net12'):
        # 全连接
        net = tf.add(tf.matmul(net, get_variable('w', [net11_unit_size, net12_unit_size])),
                     get_variable('b', [net12_unit_size]))
        net = tf.nn.relu(net)
    # fc
    with tf.variable_scope('net13'):
        # 全连接
        net = tf.add(tf.matmul(net, get_variable('w', [net12_unit_size, net13_unit_size])),
                     get_variable('b', [net13_unit_size]))

    return net


# 获取网络
act = vgg_network(x, y)

# 构建损失函数，优化器，准确率评估
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=act))  # 损失函数

# 优化器
# AdamOptimizer通过使用动量（参数的移动平均数）来改善传统梯度下降，促进超参数动态调整。
# 我们可以通过创建标签错误率的摘要标量来跟踪丢失和错误率
# 一个寻找全局最优点的优化算法，引入了二次方梯度校正。
# 相比于基础SGD算法，1.不容易陷于局部优点。2.速度更快
train = tf.train.GradientDescentOptimizer(learning_rate=learn_rate).minimize(cost)

# 正确率
# y [[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0],[0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]] ->arg_max(y,1)->[0,1]
# net  y [[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0],[0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0] ]
correct_pred = tf.equal(tf.argmax(y, axis=1), tf.argmax(act, axis=1))
acc = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

四、模型的训练

# 训练
with tf.Session(config=tf.ConfigProto(log_device_placement=True)) as sess:
    # 1.初始化所有的变量（一定在变量构建之后调用初始化操作）
    tf.global_variables_initializer().run()
    # 2.迭代训练
    for epoch in range(train_epoch):
        # a.计算一次迭代batch执行的次数
        # 前面的用于训练，后面的5个批次用于测试
        total_batch = int(total_sample_number / batch_size) - 5
        # b.迭代更新
        for step in range(total_batch):
            # 获取当前批次的数据
            train_x = X[step * batch_size:step * batch_size + batch_size]
            train_y = Y[step * batch_size:step * batch_size + batch_size]
            # 模型训练
            sess.run(train, feed_dict={x: train_x, y: train_y})

            # 每更新10次，输出一下
            if step % 10 == 0:
                loss, accuracy = sess.run([cost, acc], feed_dict={x: train_x, y: train_y})
                print('迭代次数:{}, 步骤：{}, 训练集损失函数：{}, 训练集准确率：{}'.format(epoch, step, loss, accuracy))

        # 展示一下
        if epoch % 2 == 0:
            # 获取测试集数据
            test_x = X[step * batch_size:]
            test_y = Y[step * batch_size:]
            loss, test_acc = sess.run([cost, acc], feed_dict={x: test_x, y: test_y})
            print('*' * 100)
            print('【测试集】迭代次数：{}, 测试集损失函数值：{}，测试集准确率：{}'.format(epoch, loss, test_acc))

    # 3.模型保存、持久化
    saver = tf.train.Saver()
    saver.save(sess, './vgg/model_{}'.format(train_epoch))

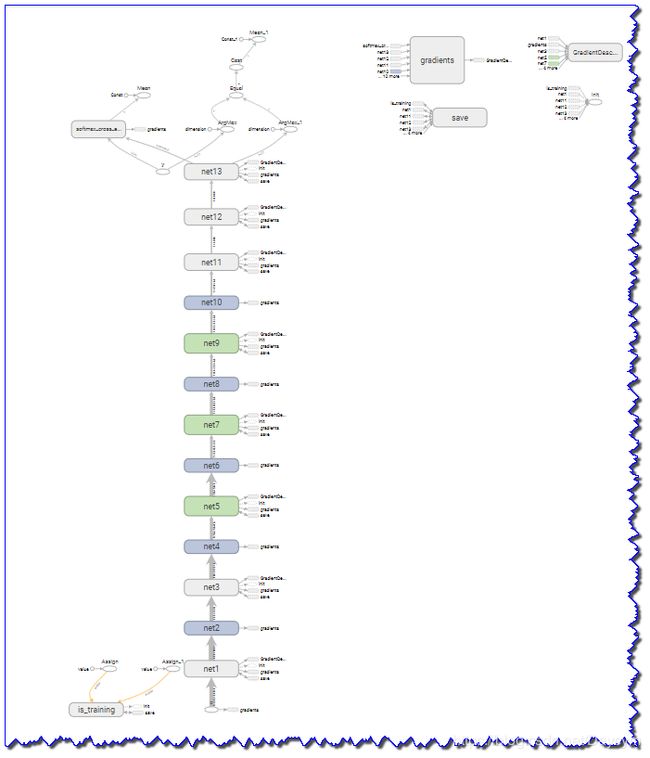
    # 模型可视化输出
    writer = tf.summary.FileWriter('./vgg/graph', tf.get_default_graph())
    writer.close()

print("End！！")

为了显示程序可行，已经最终的可视化结果，这里我只迭代了20次，感兴趣的可以尝试迭代10000次

五、模型可视化结果