RBM(Restricted Bolzmann Machines)原理

玻尔兹曼机是一种随机网络，它基于能量模型进行建模。

能量模型

我们一般认为物体的能量越高越不稳定，能量越低越趋于稳定。比如说，斜坡上的一个箱子，它位于越高的位置，则拥有更高的重力势能。能量模型把箱子停在哪个位置定义为一种状态，每个状态对应着一个能量。这个能量由能量函数来定义，箱子位于某个位置(某个位置)的概率。比如箱子位于斜坡1/2高度上的概率为p，它可以用E表示成 p=f(E) 。

能量概率模型定义通过能量函数一个概率分布：

p(x)=e−E(x)Z

Z 为配分函数：

Z=∑xe−E(x)

一个能量模型可以通过随机梯度下降来极小负似然来学习，似然为：

L(θ,D)=1N∑x(i)∈Dlogp(x(i))

目标函数：

l(θ,D)=−L(θ,D)

利用随机梯度 −∂logp(x(i))∂θ ， θ 为模型参数。
最大化这个似然函数的意义就是使模型的分布尽量地拟合训练数据的分布。

能量模型的作用

1. RBM属于一种无监督学习的方法，无监督学习的目的是最大可能地拟合训练数据。
2. 对于一组输入数据来说，如果我们不知道它属于什么分布，我们是非常难学习的。如，如果我们知道数据符合高斯分布，我们就可以确定参数，利用极大似然即可轻松地学习，但如果不知道什么分布，就无从入手。但是，统计力学的结论表明，任何概率分布都可以转换成能量模型。，这为拟合任何数据带来了可行性。
3. 在马尔科夫随机场(MRF)中，能量模型充当了两个角色：一、全局解的度量(目标函数)；二、能量最小时的解为目标解。这为能量模型提供了目标函数和目标解。

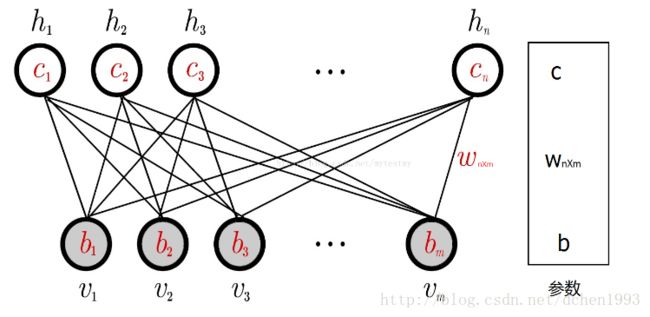
RBM结构

上图的RBM网络中有m个可视节点，n个隐藏节点，其中每个可视节点与每个隐藏节点相互关联。可视节点之间和隐藏节点之间是相互独立的。这就是RBM的概率图模型。
该网络的参数为 c,W,b ： b 为可以可视节点的偏移量， c 为隐藏节点的偏移量， W 为可视层与隐藏层之间的权重矩阵 Wx×m 。

这里为了简单描述，假设每个节点的取值为{0,1}。

编码过程

一个样本 x=(x1,x2,…,xm) 进入，经过RBM网络编码，得到这个样本的m维编码后的样本 y=(y1,y2,…,yn) ，意义为抽取了样本的n个特征。该生成的规则为：
1. 根据模型可以计算出隐藏层节点i取值为1的条件概率 p(hi=1|v)
2. 根据 p(hi=1|v) 这个概率来随机选择 hi 的取值为1还是0。
3. 对每个隐层节点执行上述操作。

解码过程

与编码过程同理，生成规则为：
1. 根据模型可以计算出可视层节点i取值为1的条件概率 p(vi=1|h)
2. 根据 p(vi=1|h) 这个概率来随机选择 vi 的取值为1还是0。
3. 对每个隐层节点执行上述操作。

概率的计算

能量模型需要定义一个能量函数，RBM的能量函数为：

E(v,h)=−∑i=1n∑j=1mwijhivj−∑j=1mbjvj−∑i=1ncihi

这个能量函数的意义是：每个可视节点和隐藏节点之间的连接都有一个能量。
还有一个解释，叫做专家乘积系统(POE, product of expert)，是Hinton发明的。他把每个隐藏节点当做一个专家，每个专家都能对可视节点的状态分布产生影响，可能单个“专家”对可视节点的状态分布不够强，但是所有的“专家”的观察结果连乘起来就够强了。

为了引入概率，定义可视节点和隐藏节点的联合概率：

p(v,h)=e−E(v,h)∑v,he−E(v,h)

其热力学解释在这里就不做解释。

有了联合概率，就可以得到条件概率和边缘概率：

P(v)=∑he−E(v,h)∑v,he−E(v,h)

P(h)=∑ve−E(v,h)∑v,he−E(v,h)

P(v|h)=e−E(v,h)∑ve−E(v,h)

P(h|v)=e−E(v,h)∑he−E(v,h)

极大似然

上面得到了一个样本和其对应编码的联合概率，也就得到了Gibbs分布的概率密度函数。

RBM求解的目标就是——让RBM网络表示的Gibbs分布最大可能的拟合训练数据（分布）。

似然函数为：

L(θ,D)=1N∑x(i)∈Dlogp(x(i))

函数的意义就是模型分布与训练数据分布的相似性。

为什么可以转化为极大似然来求解？
意义就是：当RBM网络训练完成后，如果让这个RBM网络随机发生若干次状态（当然一个状态是由(v,h)组成的），这若干次状态中，可视节点部分（就是v）出现训练样本的概率要最大。即在反编码（从隐藏节点到可视节点的编码过程）过程中，能使训练样本出现的概率最大，也就是使得反编码的误差尽最大的可能最小。
如，一个样本(1,0,1,0,1)编码到(0,1,1)，那么，(0,1,1)从隐藏节点反编码到可视节点的时候也要大概率地编码到(1,0,1,0,1)。
这就可以准确地将样本数据映射到n维的特征中而尽可能地减少损失。

求解极大似然

求解极大似然的方法一般为梯度上升，这里也不例外。

梯度可写为：

∂L(θ)∂θ=∑v∂lnp(v)∂θ

对于每个 lnp(v) :

lnp(x)=ln∑he−E(v,h)∑v,he−E(v,h)=ln(∑he−E(v,h))−ln(∑v,he−E(v,h))

∂lnp(x)∂θ=∑he−E(v,h)(−∂E(v,h)∂θ)∑he−E(v,h)−∑v,he−E(v,h)(−∂E(v,h)∂θ)∑v,he−E(v,h)=∑h(p(h|v)(−∂E(v,h)∂θ))−∑v,h(p(v,h)(−∂E(v,h)∂θ))=Ep(h|v)[−∂E(v,h)∂θ]−Ep(h,v)[−∂E(v,h)∂θ]

可见，最后可转化成两个期望，第一项为 −∂E(v,h)∂θ 在概率 p(h|v) 下的期望，第二项为 −∂E(v,h)∂θ 在概率 p(v,h) 下的期望。

下面对参数 c,W,b 分别求导：

∂lnp(x)∂wij=∑h(p(h|v)(−∂E(v,h)∂wij))−∑v,h(p(v,h)(−∂E(v,h)∂wij))=∑hp(h|v)hivj−∑v,hp(v,h)hivj=∑hp(h|v)hivj−∑vp(v)∑hp(h|v)hivj=p(hi=1|v)vj−∑vp(v)p(hi=1|v)vj

∂lnp(x)∂bj=∑h(p(h|v)(−∂E(v,h)∂bj))−∑v,h(p(v,h)(−∂E(v,h)∂bj))=∑hp(h|v)vj−∑v,hp(v,h)vj=∑hp(h|v)vj−∑vp(v)∑hp(h|v)vj=vj−∑vp(v)vj

∂lnp(x)∂ci=∑h(p(h|v)(−∂E(v,h)∂ci))−∑v,h(p(v,h)(−∂E(v,h)∂ci))=∑hp(h|v)hi−∑v,hp(v,h)hi=∑hp(h|v)hi−∑vp(v)∑hp(h|v)hi=p(hi=1|v)−∑vp(v)p(hi=1|v)

其中 p(v,h)=p(h|v)p(v) ，条件概率：

p(vj=1|h)=∑vk≠jp(vj=1,vk≠j,h)∑vp(v,h)=σ(∑i=1nwijhi+bj)

可以轻易求解。

p(hi=1|v)∑hk≠ip(hi=1,hk≠i,v)∑hp(v,h)=σ(∑j=1mwijvj+ci)

需要遍历所有可能的v值，然后根据梯度计算几个梯度的值，这样做很麻烦，但是我们可以通过对训练样本抽样得到符合模型Gibbs分布的样本，然后直接用这些样本估算以上条件概率。

对每个训练样本x，都用某种抽样方法抽取一个它对应的符合RBM网络表示的Gibbs分布的样本（对应的意思就是符合参数确定的Gibbs分布p(x)的），假如叫y；那么，对于整个的训练集 {x1,x2,…xl} 来说，就得到了一组符合RBM网络表示的Gibbs分布的样本 {y1,y2,…,yl} ，然后拿这组样本去估算第二项，那么梯度就可以用下面的公式来近似了:

∂lnp(x)∂wij=p(hi=1|v)vj−∑vp(v)p(hi=1|v)vj=p(hi=1|v)vj−1l∑k=1lp(hi=1|vyk)vyk

∂lnp(x)∂bj=vj−∑vp(v)vj=vj−1l∑k=1lvyk

∂lnp(x)∂ci=p(hi=1|v)−∑vp(v)p(hi=1|v)=p(hi=1|v)−1l∑k=1lp(hi=1|vyk)

其中 yk 表示第k个训练样本对应RBM网络表示的Gibbs分布的样本。

这样梯度就出来了。

为什么需要抽样得到符合模型Gibbs分布的样本？因为公式中需要用到关于模型的期望，不能直接用训练样本，因为训练样本的分布不一定符合模型Gibbs分布，只有符合这个分布的样本才能拿来算期望。

抽样方法

在Hinton教授还没提取CD-k之前，RBM的抽样问题是用Gibbs采样解决的。

我们有了上面的条件概率，我们就可以交替地进行下面的采样：
h0∼p(h|v0) v1∼p(v|h0)
h1∼p(h|v1) v2∼p(v|h1)
……， vk+1∼p(v|hk)

在抽样步数k足够大的情况下，就可以获得符合RBM模型Gibbs分布的样本，得到这些样本就可以计算梯度的第二项了。

但是每个样本都进行k步的抽样，计算量会很大，所以Hinton教授提出了一个简化的版本，叫做CD-k（对比散度）。与Gibbs抽样不同，Hinton教授指出当使用训练样本初始化 v0 的时候，仅需要较少的抽样步数（一般就一步）就可以得到足够好的近似。

Reference

http://blog.csdn.net/mytestmy/article/details/9150213/
http://deeplearning.net/tutorial/rbm.html