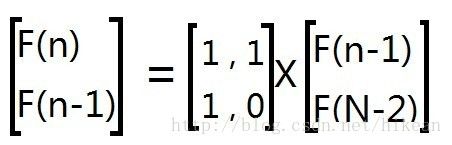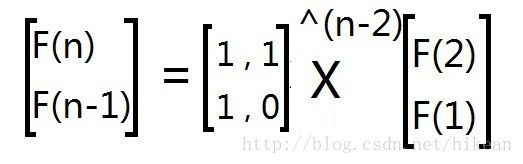- 用OpenCV标定相机内参应用示例(C++和Python)
下面是一个完整的使用OpenCV进行相机内参标定(CameraCalibration)的示例,包括C++和Python两个版本,基于棋盘格图案标定。一、目标:相机标定通过拍摄多张带有棋盘格图案的图像,估计相机的内参:相机矩阵(内参)K畸变系数distCoeffs可选外参(R,T)标定精度指标(如重投影误差)二、棋盘格参数设置(根据自己的棋盘格设置):棋盘格角点数:9x6(内角点,9列×6行);每个
- centos7安装 mysql5.7(安装包)
heiPony
linuxmysqlmariadbcentosmysql
一.卸载centos7自带数据库查看系统自带的Mariadbrpm-qa|grepmariadbmariadb-libs-5.5.44-2.el7.centos.x86_64卸载rpm-e--nodepsmariadb-libs-5.5.44-2.el7.centos.x86_64删除etc目录下的my.cnfrm/etc/my.cnf二.检查mysql是否存在(有就卸载,删除相关文件)rpm-q
- EMQX 社区版单机和集群部署
pcj_888
MQTTMQTTEMQ
EMQ支持Docker,宿主机,k8s部署;支持单机或集群部署。以下给出EMQX社区版单机和集群部署方法1.Docker单机部署官方推荐最小配置:2核4G下载容器镜像dockerpullemqx/emqx:5.3.2启动容器dockerrun-d--nameemqx\-p1883:1883\-p8083:8083\-p8883:8883\-p8084:8084\-p18083:18083\emqx
- Vue3+Vite+TS+Axios整合详细教程
老马聊技术
VueViteTSvue.js
1.Vite简介Vite是新一代的前端构建工具,在尤雨溪开发Vue3.0的时候诞生。类似于Webpack+Webpack-dev-server。其主要利用浏览器ESM特性导入组织代码,在服务器端按需编译返回,完全跳过了打包这个概念,服务器随起随用。生产中利用Rollup作为打包工具,号称下一代的前端构建工具。vite是一种新型的前端构建工具,能够显著的提升前端开发者的体验。它主要有俩部分组成:一个
- Anaconda 详细下载与安装教程
Anaconda详细下载与安装教程1.简介Anaconda是一个用于科学计算的开源发行版,包含了Python和R的众多常用库。它还包括了conda包管理器,可以方便地安装、更新和管理各种软件包。2.下载Anaconda2.1访问官方网站首先,打开浏览器,访问Anaconda官方网站。2.2选择适合的版本在页面中,你会看到两个主要的下载选项:AnacondaIndividualEdition:适用于
- C++设计模式:简单工厂、工厂方法、抽象工厂
起个别名
C++算法c++
1.工厂模式的特点在我们现实生活中,买馒头和自己蒸馒头、去饭店点一份大盘鸡和自己养鸡,杀鸡,做大盘鸡,这是全然不同的两种体验:自己做麻烦,而且有失败的风险,需要自己承担后果。买现成的,可以忽略制作细节,方便快捷并且无风险,得到的肯定是美味的食物。对于后者,就相当于是一个加工厂,通过这个工厂我们就可以得到想要的东西,在程序设计中,这种模式就叫做工厂模式,工厂生成出的产品就是某个类的实例,也就是对象。
- npm proxy setting
kjndppl
[Node.jsJavaScriptnpmhttpsproxypassword
清理npmconfigdeletehttp-proxynpmconfigdeletehttps-proxy具体设置步骤如下:1.执行npmconfig后,将看到下一行提示信息npmconfigls-ltoshowalldefaults.2.执行npmconfigls-l后,在一大长串的settign中找出userconfig项(大概位于倒数第4项)[b]userconfig[/b]="C:\\Us
- kube-scheduler 抢占机制
分享放大价值
kubernetes源码分析kuberneteskube-scheduler抢占
当pod调度失败后,会在PostFilter扩展点执行抢占流程,下面分析相关的代码实现抢占接口//PodNominatorabstractsoperationstomaintainnominatedPods.typePodNominatorinterface{//将pod加入抢占成功的node中AddNominatedPod(pod*PodInfo,nodeNamestring)//将pod从no
- Linux/Centos7离线安装并配置MySQL 5.7
有事开摆无事百杜同学
LInux/CentOS7linuxmysql运维
Linux/Centos7离线安装并配置MySQL5.7超详细教程一、环境准备1.下载MySQL5.7离线包2.使用rpm工具卸载MariaDB(避免冲突)3.创建系统级别的MySQL专用用户二、安装与配置1.解压并重命名MySQL目录2.创建数据目录和配置文件3.设置目录权限4.初始化MySQL5.配置启动脚本6.配置环境变量三、启动与验证1.启动MySQL服务2.获取初始密码3.登录并修改密码
- docker安装node部分问题
自律的蜗牛
docker容器node.js
sudonlatestsudo:n:commandnotfound如果运行sudonlatest时出现:sudo:n:commandnotfound说明n版本管理工具未安装或未添加到PATH环境变量。解决方案1️⃣先检查n是否已安装运行:whichn或者:command-vn如果有输出/usr/local/bin/n,说明n已安装,但可能需要sudo访问。如果没有任何输出,说明n没有安装,跳到方法
- 本地包解决npm error code E404
雅痞yuppie
npm前端node.js
这个错误提示表明npm找不到名为create-vue-admin-cli的包。这是因为你开发的CLI工具还没有发布到npm官方注册表。要解决这个问题,有两种方法:方法一:使用本地开发模式测试1.确保你的CLI已正确链接到全局在你的vue-admin-cli项目根目录下执行:npmlink这会在全局环境中创建一个符号链接,指向你本地的CLI项目。2.使用本地链接的CLI创建项目直接使用命令:vue-
- python中 @注解 及内置注解 的使用方法总结以及完整示例
慧一居士
Pythonpython
在Python中,装饰器(Decorator)使用@符号实现,是一种修改函数/类行为的语法糖。它本质上是一个高阶函数,接受目标函数作为参数并返回包装后的函数。Python也提供了多个内置装饰器,如@property、@staticmethod、@classmethod等。一、核心概念装饰器本质:@decorator等价于func=decorator(func)执行时机:在函数/类定义时立即执行装饰
- Java特性之设计模式【责任链模式】
Naijia_OvO
Java特性java设计模式责任链模式
一、责任链模式概述顾名思义,责任链模式(ChainofResponsibilityPattern)为请求创建了一个接收者对象的链。这种模式给予请求的类型,对请求的发送者和接收者进行解耦。这种类型的设计模式属于行为型模式在这种模式中,通常每个接收者都包含对另一个接收者的引用。如果一个对象不能处理该请求,那么它会把相同的请求传给下一个接收者,依此类推主要解决:职责链上的处理者负责处理请求,客户只需要将
- windows安装pnpm后报错:pnpm : 无法将“pnpm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。
Ithao2
Vuenpm前端node.js
使用npm方式安装pnpm,命令如下:npminstall-gpnpm安装完以后,执行pnpm-v查看版本号:pnpm-v执行完发现报错:pnpm:无法将“pnpm”项识别为cmdlet、函数、脚本文件或可运行程序的名称。尝试配置环境变量,重启后均不生效。解决方案:使用PowerShell进行安装1.以管理员用户打开PowerShell,执行如下命令:iwrhttps://get.pnpm.io/
- Python中的静态方法和类方法详解
在Python中,`@staticmethod`和`@classmethod`是两种装饰器,它们用于定义类中的方法,但是它们的行为和用途有所不同。###@staticmethod`@staticmethod`装饰器用于定义一个静态方法。静态方法不接收类或实例的引用作为第一个参数,因此它不能访问类的状态或实例的状态。静态方法可以看作是与类关联的普通函数,但它们可以通过类名直接调用。classMath
- Linux操作系统磁盘管理
CZZDg
linux运维服务器
目录一.硬盘介绍1.硬盘的物理结构2.CHS编号3.磁盘存储划分4.开机流程5.要点6.磁盘存储数据的形式二.Linux文件系统1.根文件系统2.虚拟文件系统3.真文件系统4.伪文件系统三.磁盘分区与挂载1.磁盘分区方式2.分区命令3.查看与识别命令4.格式化命令5.挂载命令四.LVM逻辑卷1.概述2.管理命令五.磁盘配额1.概述usrquota:支持对用户的磁盘配额grpquota:支持对组的磁
- 计算机网络技术
CZZDg
计算机网络
目录一.网络概述1.网络的概念2.网络发展是3.网络的四要素4.网络功能5.网络类型6.网络协议与标准7.网络中常见的概念8.网络拓补结构二.网络模型1.分层思想2.OSI七层模型3.TCP/IP五层模型4.数据的封装与解封装过程三.IP地址1.进制转换2.IP地址定义3.IP地址组成成分4.IP地址分类5.地址划分6、相关概念一.网络概述1.网络的概念两个主机通过传输介质和通信协议实现通信和资源
- cesium添加原生MVT矢量瓦片方案
zhu_zhu_xia
cesiumvuearcgiscesiumwebgljavascript
项目中需要基于cesium接入mvt格式的服务并支持属性拾取查询,通过一系列预研测试,最后选择cesium-mvt-imagery-provider开源插件完成,关键源码信息如下:npmicesiumcesium-mvt-imagery-provider//安装依赖包//加载图层importCesiumMVTImageryProviderfrom"cesium-mvt-imagery-provid
- npm 切换 node 版本 和npm的源
爱敲代码的小冰
npm前端node.js
在开发过程中,不同项目可能需要不同版本的Node.js,同时于由XX原因,我们需要切换npm的源。这时如果需要切换node版本或者npm的源,我们可以使用以下方法。使用nvm切换Node版本1、安装npminstallnvm-g2、使用#列出所有可用版本nvmlist-remote#安装指定版本nvminstall16.15.1#使用指定版本nvmuse16.15.1#查看当前使用的版本nvmcu
- Python中类静态方法:@classmethod/@staticmethod详解和实战示例
在Python中,类方法(@classmethod)和静态方法(@staticmethod)是类作用域下的两种特殊方法。它们使用装饰器定义,并且与实例方法(deffunc(self))的行为有所不同。1.三种方法的对比概览方法类型是否访问实例(self)是否访问类(cls)典型用途实例方法✅是❌否访问对象属性类方法@classmethod❌否✅是创建类的替代构造器,访问类变量等静态方法@stati
- 日历插件-FullCalendar的详细使用
老马聊技术
JavaScript前端javascript
一、介绍FullCalendar是一个功能强大、高度可定制的JavaScript日历组件,用于在网页中显示和管理日历事件。它支持多种视图(月、周、日等),可以轻松集成各种框架,并提供丰富的事件处理功能。二、实操案例具体代码如下:FullCalendar日期选择body{font-family:Arial,sans-serif;margin:20px;}#calendar{max-width:900
- EasyCwmp源码分析与接口实现详解:深入理解源码架构,掌握核心接口
EasyCwmp源码分析与接口实现详解:深入理解源码架构,掌握核心接口去发现同类优质开源项目:https://gitcode.com/在开源项目中,寻找一款能够提升开发效率、简化流程的工具是每个开发者的追求。今天,我们要介绍的这款开源项目EasyCwmp,正是为了帮助开发者深入了解源码架构,掌握核心接口实现,从而加速项目开发进程。以下是关于EasyCwmp源码分析与接口实现详解的项目推荐文章。项目
- OpenWebUI(12)源码学习-后端constants.py常量定义文件
青苔猿猿
AI大模型openwebuiconstants常量定义
目录文件名:`constants.py`功能概述:主要功能点详解1.**MESSAGES枚举类**2.**WEBHOOK_MESSAGES枚举类**3.**ERROR_MESSAGES枚举类**✅默认错误模板✅认证与用户相关错误✅资源冲突与重复错误✅验证失败类错误✅权限限制类错误✅文件上传与格式错误✅模型与API错误✅请求频率与安全限制✅数据库与配置错误4.**TASKS枚举类**✅总结实际应用场
- Kafka系列之:Dead Letter Queue死信队列DLQ
快乐骑行^_^
KafkaKafka系列DeadLetterQueue死信队列DLQ
Kafka系列之:DeadLetterQueue死信队列DLQ一、死信队列二、参数errors.tolerance三、创建死信队列主题四、在启用安全性的情况下使用死信队列更多内容请阅读博主这篇博客:Kafka系列之:KafkaConnect深入探讨-错误处理和死信队列一、死信队列死信队列(DLQ)仅适用于接收器连接器。当一条记录以JSON格式到达接收器连接器时,但接收器连接器配置期望另一种格式,如
- 基于Python的健身数据分析工具的搭建流程day1
weixin_45677320
python开发语言数据挖掘爬虫
基于Python的健身数据分析工具的搭建流程分数据挖掘、数据存储和数据分析三个步骤。本文主要介绍利用Python实现健身数据分析工具的数据挖掘部分。第一步:加载库加载本文需要的库,如下代码所示。若库未安装,请按照python如何安装各种库(保姆级教程)_python安装库-CSDN博客https://blog.csdn.net/aobulaien001/article/details/133298
- tcpdump交叉编译
weixin_45673259
tcpdump测试工具网络
1.下载路径官网:https://www.tcpdump.org/2.编译解压:tar-xflibpcap-1.10.4.tar.xztar-xftcpdump-4.99.4.tar.xz编译libpcap./configure--host=mips-v720s229-linux--target=mips-v720s229-linuxCC=/opt/A1/mips-gcc720-uclibc229
- 消息中间件巡检
搬砖小常
消息中间件运维笔记RocketMQkafka中间件巡检运维
除资源使用情况外,消息中间件RocketMQ、kafka还可以巡检哪些?一、RocketMQ巡检1、检查broker写入耗时是否有压力2、检查brokerbusy的数量与频率3、主题发送TPS、发送错误率巡检4、从节点消费情况检查5、集群各broker消息流转情况巡检二、Kafka巡检1、检查是否有分区发生ISR频繁扩张收缩2、检查分区leader选举值是否处于正常水平3、检查controller
- cvc降噪和主动降噪_音频知识:CVC降噪和ANC主动降噪的区别和应用
汪国
cvc降噪和主动降噪
原标题:音频知识:CVC降噪和ANC主动降噪的区别和应用降噪,对于需要长时间戴耳机的人群来讲,起到了很好的保护作用。然而在购买蓝牙耳机时总会听到商家在宣传耳机所具备的CVC、ANC降噪功能,尽管听过很多商家描述,有些小伙伴依然不是很明白这两者之间的区别以及应用。现在简单和大家介绍这两个看不懂的降噪名词。CVC降噪(ClearVoiceCapture)是通话软件降噪技术。工作原理是是通过耳机内置的消
- RocketMQ 基础教程-应用篇-死信队列
码炫课堂-码哥
rocketmq专题rocketmqjava
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬学习必须往深处挖,挖的越深,基础越扎实!阶段1、深入多线程阶段2、深入多线程设计模式阶段3、深入juc源码解析阶段4、深入jdk其余源码解析
- 入门html这篇文章就够了
ξ流ぁ星ぷ132
html前端
HTML笔记文章目录HTML笔记html介绍什么是htmlhtml的作用HTML标签介绍常用标签标签and标签and标签u标签del删除线br标签用于换行pre标签,预处理标签span标签div标签sub标签andsup标签hr标签h1,h2...h6标签:HTML5中的语义标签:特殊字符img标签a标签第一种用法:超链接第二种用法:锚点video标签表格标签:form标签input标签selec
- jquery实现的jsonp掉java后台
知了ing
javajsonpjquery
什么是JSONP?
先说说JSONP是怎么产生的:
其实网上关于JSONP的讲解有很多,但却千篇一律,而且云里雾里,对于很多刚接触的人来讲理解起来有些困难,小可不才,试着用自己的方式来阐释一下这个问题,看看是否有帮助。
1、一个众所周知的问题,Ajax直接请求普通文件存在跨域无权限访问的问题,甭管你是静态页面、动态网页、web服务、WCF,只要是跨域请求,一律不准;
2、
- Struts2学习笔记
caoyong
struts2
SSH : Spring + Struts2 + Hibernate
三层架构(表示层,业务逻辑层,数据访问层) MVC模式 (Model View Controller)
分层原则:单向依赖,接口耦合
1、Struts2 = Struts + Webwork
2、搭建struts2开发环境
a>、到www.apac
- SpringMVC学习之后台往前台传值方法
满城风雨近重阳
springMVC
springMVC控制器往前台传值的方法有以下几种:
1.ModelAndView
通过往ModelAndView中存放viewName:目标地址和attribute参数来实现传参:
ModelAndView mv=new ModelAndView();
mv.setViewName="success
- WebService存在的必要性?
一炮送你回车库
webservice
做Java的经常在选择Webservice框架上徘徊很久,Axis Xfire Axis2 CXF ,他们只有一个功能,发布HTTP服务然后用XML做数据传输。
是的,他们就做了两个功能,发布一个http服务让客户端或者浏览器连接,接收xml参数并发送xml结果。
当在不同的平台间传输数据时,就需要一个都能解析的数据格式。
但是为什么要使用xml呢?不能使json或者其他通用数据
- js年份下拉框
3213213333332132
java web ee
<div id="divValue">test...</div>测试
//年份
<select id="year"></select>
<script type="text/javascript">
window.onload =
- 简单链式调用的实现技术
归来朝歌
方法调用链式反应编程思想
在编程中,我们可以经常遇到这样一种场景:一个实例不断调用它自身的方法,像一条链条一样进行调用
这样的调用你可能在Ajax中,在页面中添加标签:
$("<p>").append($("<span>").text(list[i].name)).appendTo("#result");
也可能在HQ
- JAVA调用.net 发布的webservice 接口
darkranger
webservice
/**
* @Title: callInvoke
* @Description: TODO(调用接口公共方法)
* @param @param url 地址
* @param @param method 方法
* @param @param pama 参数
* @param @return
* @param @throws BusinessException
- Javascript模糊查找 | 第一章 循环不能不重视。
aijuans
Way
最近受我的朋友委托用js+HTML做一个像手册一样的程序,里面要有可展开的大纲,模糊查找等功能。我这个人说实在的懒,本来是不愿意的,但想起了父亲以前教我要给朋友搞好关系,再加上这也可以巩固自己的js技术,于是就开始开发这个程序,没想到却出了点小问题,我做的查找只能绝对查找。具体的js代码如下:
function search(){
var arr=new Array("my
- 狼和羊,该怎么抉择
atongyeye
工作
狼和羊,该怎么抉择
在做一个链家的小项目,只有我和另外一个同事两个人负责,各负责一部分接口,我的接口写完,并全部测联调试通过。所以工作就剩下一下细枝末节的,工作就轻松很多。每天会帮另一个同事测试一些功能点,协助他完成一些业务型不强的工作。
今天早上到公司没多久,领导就在QQ上给我发信息,让我多协助同事测试,让我积极主动些,有点责任心等等,我听了这话,心里面立马凉半截,首先一个领导轻易说
- 读取android系统的联系人拨号
百合不是茶
androidsqlite数据库内容提供者系统服务的使用
联系人的姓名和号码是保存在不同的表中,不要一下子把号码查询来,我开始就是把姓名和电话同时查询出来的,导致系统非常的慢
关键代码:
1, 使用javabean操作存储读取到的数据
package com.example.bean;
/**
*
* @author Admini
- ORACLE自定义异常
bijian1013
数据库自定义异常
实例:
CREATE OR REPLACE PROCEDURE test_Exception
(
ParameterA IN varchar2,
ParameterB IN varchar2,
ErrorCode OUT varchar2 --返回值,错误编码
)
AS
/*以下是一些变量的定义*/
V1 NUMBER;
V2 nvarc
- 查看端号使用情况
征客丶
windows
一、查看端口
在windows命令行窗口下执行:
>netstat -aon|findstr "8080"
显示结果:
TCP 127.0.0.1:80 0.0.0.0:0 &
- 【Spark二十】运行Spark Streaming的NetworkWordCount实例
bit1129
wordcount
Spark Streaming简介
NetworkWordCount代码
/*
* Licensed to the Apache Software Foundation (ASF) under one or more
* contributor license agreements. See the NOTICE file distributed with
- Struts2 与 SpringMVC的比较
BlueSkator
struts2spring mvc
1. 机制:spring mvc的入口是servlet,而struts2是filter,这样就导致了二者的机制不同。 2. 性能:spring会稍微比struts快。spring mvc是基于方法的设计,而sturts是基于类,每次发一次请求都会实例一个action,每个action都会被注入属性,而spring基于方法,粒度更细,但要小心把握像在servlet控制数据一样。spring
- Hibernate在更新时,是可以不用session的update方法的(转帖)
BreakingBad
Hibernateupdate
地址:http://blog.csdn.net/plpblue/article/details/9304459
public void synDevNameWithItil()
{Session session = null;Transaction tr = null;try{session = HibernateUtil.getSession();tr = session.beginTran
- 读《研磨设计模式》-代码笔记-观察者模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
import java.util.Observable;
import java.util.Observer;
/**
* “观
- 重置MySQL密码
chenhbc
mysql重置密码忘记密码
如果你也像我这么健忘,把MySQL的密码搞忘记了,经过下面几个步骤就可以重置了(以Windows为例,Linux/Unix类似):
1、关闭MySQL服务
2、打开CMD,进入MySQL安装目录的bin目录下,以跳过权限检查的方式启动MySQL
mysqld --skip-grant-tables
3、新开一个CMD窗口,进入MySQL
mysql -uroot
- 再谈系统论,控制论和信息论
comsci
设计模式生物能源企业应用领域模型
再谈系统论,控制论和信息论
偶然看
- oracle moving window size与 AWR retention period关系
daizj
oracle
转自: http://tomszrp.itpub.net/post/11835/494147
晚上在做11gR1的一个awrrpt报告时,顺便想调整一下AWR snapshot的保留时间,结果遇到了ORA-13541这样的错误.下面是这个问题的发生和解决过程.
SQL> select * from v$version;
BANNER
-------------------
- Python版B树
dieslrae
python
话说以前的树都用java写的,最近发现python有点生疏了,于是用python写了个B树实现,B树在索引领域用得还是蛮多了,如果没记错mysql的默认索引好像就是B树...
首先是数据实体对象,很简单,只存放key,value
class Entity(object):
'''数据实体'''
def __init__(self,key,value)
- C语言冒泡排序
dcj3sjt126com
算法
代码示例:
# include <stdio.h>
//冒泡排序
void sort(int * a, int len)
{
int i, j, t;
for (i=0; i<len-1; i++)
{
for (j=0; j<len-1-i; j++)
{
if (a[j] > a[j+1]) // >表示升序
- 自定义导航栏样式
dcj3sjt126com
自定义
-(void)setupAppAppearance
{
[[UILabel appearance] setFont:[UIFont fontWithName:@"FZLTHK—GBK1-0" size:20]];
[UIButton appearance].titleLabel.font =[UIFont fontWithName:@"FZLTH
- 11.性能优化-优化-JVM参数总结
frank1234
jvm参数性能优化
1.堆
-Xms --初始堆大小
-Xmx --最大堆大小
-Xmn --新生代大小
-Xss --线程栈大小
-XX:PermSize --永久代初始大小
-XX:MaxPermSize --永久代最大值
-XX:SurvivorRatio --新生代和suvivor比例,默认为8
-XX:TargetSurvivorRatio --survivor可使用
- nginx日志分割 for linux
HarborChung
nginxlinux脚本
nginx日志分割 for linux 默认情况下,nginx是不分割访问日志的,久而久之,网站的日志文件将会越来越大,占用空间不说,如果有问题要查看网站的日志的话,庞大的文件也将很难打开,于是便有了下面的脚本 使用方法,先将以下脚本保存为 cutlog.sh,放在/root 目录下,然后给予此脚本执行的权限
复制代码代码如下:
chmo
- Spring4新特性——泛型限定式依赖注入
jinnianshilongnian
springspring4泛型式依赖注入
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- centOS安装GCC和G++
liuxihope
centosgcc
Centos支持yum安装,安装软件一般格式为yum install .......,注意安装时要先成为root用户。
按照这个思路,我想安装过程如下:
安装gcc:yum install gcc
安装g++: yum install g++
实际操作过程发现,只能有gcc安装成功,而g++安装失败,提示g++ command not found。上网查了一下,正确安装应该
- 第13章 Ajax进阶(上)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- How to determine BusinessObjects service pack and fix pack
blueoxygen
BO
http://bukhantsov.org/2011/08/how-to-determine-businessobjects-service-pack-and-fix-pack/
The table below is helpful. Reference
BOE XI 3.x
12.0.0.
y BOE XI 3.0 12.0.
x.
y BO
- Oracle里的自增字段设置
tomcat_oracle
oracle
大家都知道吧,这很坑,尤其是用惯了mysql里的自增字段设置,结果oracle里面没有的。oh,no 我用的是12c版本的,它有一个新特性,可以这样设置自增序列,在创建表是,把id设置为自增序列
create table t
(
id number generated by default as identity (start with 1 increment b
- Spring Security(01)——初体验
yang_winnie
springSecurity
Spring Security(01)——初体验
博客分类: spring Security
Spring Security入门安全认证
首先我们为Spring Security专门建立一个Spring的配置文件,该文件就专门用来作为Spring Security的配置