高斯消去法解线性方程组C++实现

       一．问题分析：高斯消去法解线性方程组主要面对的问题是矩阵的运算，所以可以定义一个矩阵类Matrix类作为基类，然后由矩阵类Matrix类派生出一个线性方程组类LinearEqu类。

       二．矩阵功能分析：（1）Matrix类处理n*n的方阵，方阵用一个一维数组存放，矩阵类Matrix的数据成员包括数组的首地址和矩阵长度n，函数成员有设置矩阵的值setMatrix()和显示矩阵printMatrix()。（2）LinearEqu类除了由矩阵Matrix继承过来的存放矩阵A的成员之外，还包括存放解向量X和方程右端向量b的数组的首地址。LinearEqu类的主要操作有方程组设置setLinearEqu(),显示printLinearEqu(),求解solve()及输出方程组的解printSolution()

注：Matrix类只对矩阵进行处理，不掺杂任何方程思想，LinearEqu类利用矩阵类来求解方程

       三．画出UML图

                          

         四.代码

             Matrix.h文件

#ifndef _MATRIX_H_
#define _MATRIX_H_
class Matrix{
public:
	Matrix(int size = 2);
	~Matrix();
	void setMatrix(const double* values);//矩阵赋初值
	void printMatrix() const;//显示矩阵
	int getSize() const{ return size; }//得到矩阵大小
	double &element(int i, int j){ return elements[i*size + j]; }
	double element(int i, int j) const{ return elements[i*size + j]; }//取矩阵的第i行第j列的元素
private:
	int size;
	double* elements;//矩阵存放数组首地址
};
#endif

 Matrix.cpp文件，实现Matrix.h中声明的函数 

#include"Matrix.h"
#include
using namespace std;

Matrix::Matrix(int size /*= 2*/) :size(size){//Matrix类的构造函数的实现
	elements = new double[size*size];//动态内存分配
}

Matrix::~Matrix(){//矩阵Matrix的析构函数
	delete[] elements;//内存释放
}

void Matrix::setMatrix(const double* values){//矩阵赋初值
	for (int i = 0; i < size*size; i++)
		elements[i] = values[i];
}

void Matrix::printMatrix() const{//显示矩阵
	cout << "The Matrix is:" << endl;
	for (int i = 0; i < size; i++){
		for (int j = 0; j < size; j++)
			cout << element(i, j) << " ";
		cout << endl;
	}
}

 LinearEqu.h文件

#ifndef _LINEAREQU_H_
#define _LINEAREQU_H_
#include"Matrix.h"
class LinearEqu :public Matrix{
public:
	LinearEqu(int size = 2);
	~LinearEqu();
	void setLinearEqu(const double* a, const double* b);//方程赋值（设置线性方程组）
	//a表示的是系数矩阵，b表示的是右端矩阵
	bool solve();//全选主元高斯消去法求解方程
	void printLinearEqu() const;//显示方程
	void printSolution() const;//显示方程的解
private:
	double* sums;//方程右端向量
	double* solution;//方程的解
};
#endif

 LinearEqu.cpp文件,实现LinearEqu.h中声明的函数 

#include"LinearEqu.h"
#include
#include
using namespace std;

//用size调用基类构造函数
LinearEqu::LinearEqu(int size/*=2*/) :Matrix(size) {
	sums = new double[size];//动态内存分配
	solution = new double[size];
}

LinearEqu::~LinearEqu(){
	delete[] sums;
	delete[] solution;
}

//设置线性方程组
void LinearEqu::setLinearEqu(const double* a, const double* b){
	setMatrix(a);//调用基类函数
	for (int i = 0; i < getSize(); i++)
		sums[i] = b[i];
}

//显示线性方程组
void LinearEqu::printLinearEqu() const{
	cout << "The Line eqution is:" << endl;
	for (int i = 0; i < getSize(); i++){
		for (int j = 0; j < getSize(); j++)
			cout << element(i, j) << " ";
		cout << "     " << sums[i] << endl;
	}
	cout << endl;
}

//输出方程的解
void LinearEqu::printSolution() const{
	cout << "The Result eqution is:" << endl;
	for (int i = 0; i < getSize(); i++)
		cout << "x[" << i << "]=" << solution[i] << endl;
}

//交换两个实数
inline void swap(double &v1, double &v2){
	double temp = v1;
	v1 = v2;
	v2 = temp;
}

bool LinearEqu::solve(){//全选主元素高斯消去法求解方程
	int *js = new int[getSize()];//存储主元素所在列号的数组

	//选主元素
	for (int k = 0; k < getSize()-1; k++){
		int is;//主元素所在行号
		double max = 0;//所有元素的最大值
		for (int i = k; i < getSize(); i++){
			for (int j = k; j < getSize(); j++){
				double t = fabs(element(i, j));
				if (t > max){
					max = t;
					js[k] = j;
					is = i;
				}
			}
		}
		if (max == 0){
			delete[] js;
			return false;
		}
		else{
			//通过行列交换，把主元素交换到第k行第k列上
			if (js[k] != k)//主元素不在第k列上，交换一列
				for (int i = 0; i < getSize(); i++)
					swap(element(i, k), element(i, js[k]));
			if (is != k){//主元素不在第k行上，交换一行
				for (int j = k; j < getSize(); j++){
					swap(element(is, j), element(k, j));
					swap(sums[k], sums[is]);
				}
			}
		}

		//消去过程
		double major = element(k, k);
		for (int j = k + 1; j < getSize(); j++)
			element(k, j) /= major;
		sums[k] /= major;
		for (int i = k + 1; i < getSize(); i++){
			for (int j = k + 1; j < getSize(); j++)
				element(i, j) -= element(i, k)*element(k, j);//行之间的操作
			sums[i] -= element(i, k)*sums[k];
		}
	}
	//判断剩下的一个元素是否等于0（等于0则矩阵的秩不等于矩阵的行数，则无解）
	double d = element(getSize() - 1, getSize() - 1);
	if (fabs(d) < 1e-15){
		delete[] js;
		return false;
	}

	//求出解之前验证一下最终化简结果
	printMatrix();
	cout << "Output right end matrix:" << endl;
	for (int i = 0; i < getSize(); i++)
		cout << sums[i] << " ";
	cout << endl << endl;

	//回代过程
	solution[getSize() - 1] = sums[getSize() - 1] / d;
	for (int i = getSize() - 2; i >= 0; i--){
		double t = 0.0;
		for (int j = i + 1; j <= getSize() - 1; j++)
			t += element(i, j)*solution[j];//实际上不是单位矩阵
		solution[i] = sums[i] - t;
	}
	js[getSize() - 1] = getSize() - 1;//最后一行最后一列主元素就是本列
	for (int k = getSize() - 1; k >= 0; k--)
		if (js[k] != k) swap(solution[k], solution[js[k]]);
	delete[] js;
	return true;
}

主函数文件

#include
#include"LinearEqu.h"
using namespace std;
int main(){
	double a[] = {//方程系数矩阵
		0.2368, 0.2471, 0.2568, 1.2671,
		0.1968, 0.2071, 1.2168, 0.2271,
		0.1581, 1.1675, 0.1768, 0.1871,
		1.1161, 0.1254, 0.1397, 0.1490
	};
	double b[] = { 1.8471, 1.7471, 1.6471, 1.5471 };//方程右端项
	LinearEqu equ(4);//定义一个四元方程组对象
	equ.setLinearEqu(a, b);//设置方程组
	equ.printLinearEqu();//输出方程组
	if (equ.solve())
		equ.printSolution();
	else
		cout << "Fail" << endl;
	return 0;
}

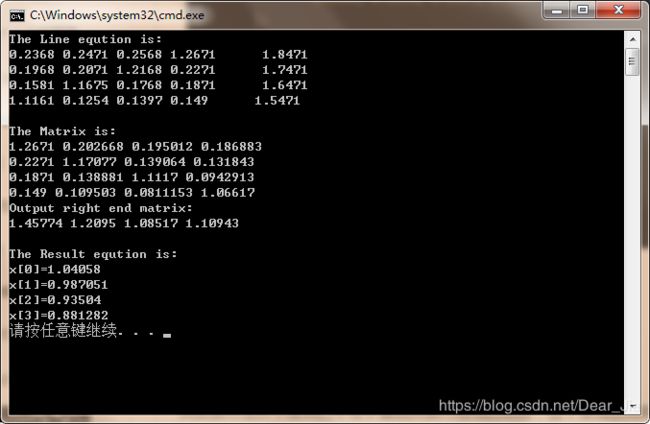
五. 结果

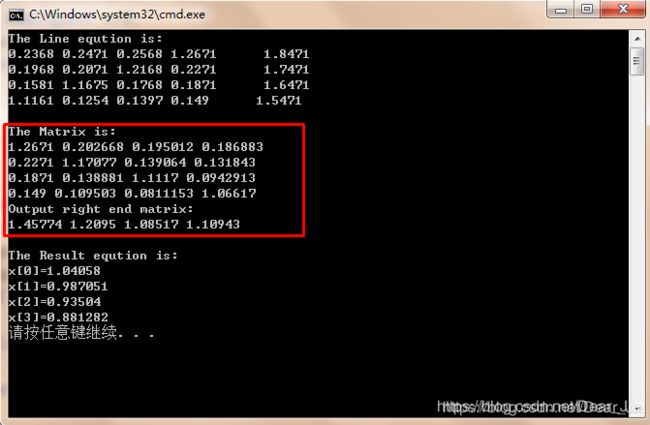
六，分析

其实该方法并不是我们平常手算矩阵解方程组的思路，这个是按照高斯消去法的逻辑将方程组矩阵一步步的转化，但是最后并没有转化为单位矩阵，而是转化为了逻辑上的阶梯矩阵，然后进一步求出解，图中红色即为最终化成的矩阵