哈夫曼编解码算法（C实现）

记得在毕业前去找工作，应聘康佳集团移动应用工程师的笔试题出了这么一道题。

传输文本字符”BADCADFEED”，只能出现”ABCDEF”这六个字符，使用以下的编码方式：

如传输字符：BADCADFEED          接收编码：001000011010000011101100100011

 

接收方可以根据每3个bit进行一次字符解码的方式还原文本传输的信息，但是这样的传输效率太低了，需要30bit才发送10个字符。如何编码来提高传输以及接收效率？？？请写出你的编码方式以及算法思想。

我当时并没有想到解决方法,GG了。最近运用到霍夫曼树，现在回想起来不就是这个算法吗，哈哈哈，太好了。在这里总结一下。

 

引入：

要提高效率，必须要从编码方式去改变，这是无疑的。这里运用了避免每一个字符都占有相同的bit位。如

如传输字符：BADCADFEED          接收编码：1001010010101001000111100 

改进编码方式之后，可以看到发送相同的字符，需要25bit位就可以表示10个字符了。这种编码明显是有很大优势的。

 

问题：这个编码方式有什么规律呢？怎么得到呢？又是如何在接收方解码的呢？下面来揭开神奇的面纱。

假定经过统计得出ABCDEF在所需传输报文出现的概率如下：

 

霍夫曼树算法： 

给定实数w1,w2,···，wt且 w1<=w2<=···<=wt           

（1）连接w1,w2为权的两片树叶，得一分支点，其权为w1+w2 ；

（2）在w1+w2, w3+···+wt中选出两个最小的权，连接它们对应的顶点（不一定都是树叶），得分支点及所带的权；

（3）重复（2），直到形成t – 1个分支点，t片树叶为止

 

或者这样描述算法：

1、给定n个数值{ v1, v2, …, vn}

2.根据这n个数值构造二叉树集合F

F = { T1, T2, …, Tn}           Ti的数据域为vi，左右子树为空

3.在F中选取两棵根结点的值最小的树作为左右子树构造一棵新的二叉树，这棵二叉树的根结点中的值为左右子树根结点中的值之和

4.在F中删除这两棵子树，并将构造的新二叉树加入F中

5.重复3和4，直到F中只剩下一个树为止。这棵树即霍夫曼树

 

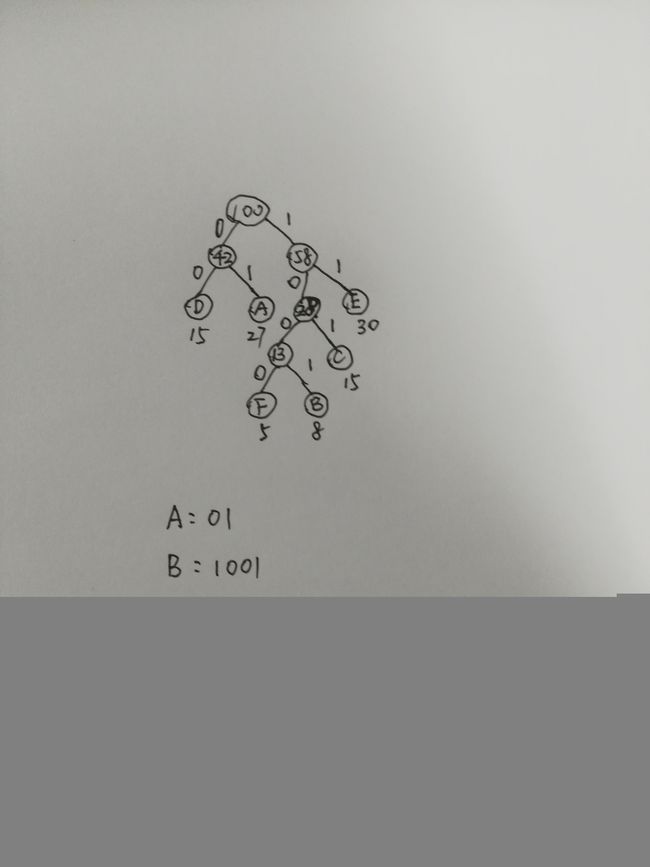
图解上面算法过程：（不想用电脑画图了，直接简单粗暴用手画一个）

Huffman树中，左边分支置为0，右边分支置为1，就行形成了每个结点的哈夫曼编码了

哈夫曼树的应用：

主要用途是实现数据压缩。在某些通讯场合，需将传送的文字转换成由二进制字符组成的字符串进行传输，也是现代压缩软件中运用到的算法的基础

测试结果：

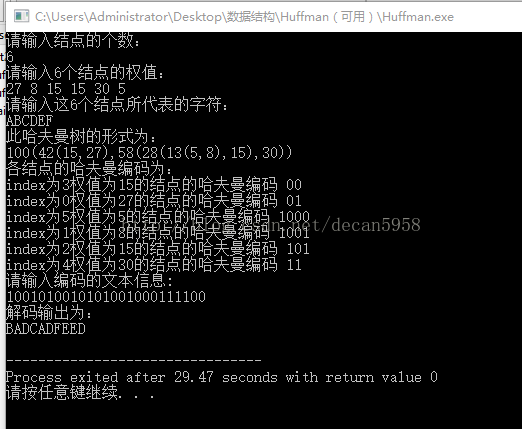
C实现代码：

// Huffman.h

#ifndef HUFFMANBITREE_H_H  
#define HUFFMANBITREE_H_H  

//数据封装 
typedef int LeafNode;  
  
// 哈夫曼树结点结构体  
typedef struct HuffmanTree  
{  
    LeafNode weight;        //结点权重 
    LeafNode index;        // index用来主要用以区分权值相同的结点，这里代表了下标  
    
    struct HuffmanTree* lchild;  
    struct HuffmanTree* rchild;  
}HuffmanNode;  

//创建哈夫曼树 
HuffmanNode* createHuffmanTree(int* Arr, int n);  

//打印哈夫曼树   
void PrintHuffmanTree(HuffmanNode* hufmTree);

// 哈夫曼编码 
void HuffmanCode(HuffmanNode* hufmTree, int depth);      // depth是哈夫曼树的深度 

//哈夫曼解码 
void HuffmanDecode(char DecodeStr[], HuffmanNode* hufmTree, char NodeStr[]);  // DecodeStr是要解码的01串，NodeStr是结点对应的字符
  
#endif  

//Huffman.c
#include   
#include  
#include 
#include "Huffman.h"

// 构建哈夫曼树  
HuffmanNode* createHuffmanTree(int* Arr, int n)  
{  
    int i, j;  
    HuffmanNode **Total_HuffmanNode, *hufmTree;  
    Total_HuffmanNode = malloc(n*sizeof(HuffmanNode));  
    
    for (i=0; iweight = Arr[i];  
        Total_HuffmanNode[i]->index = i;  
        Total_HuffmanNode[i]->lchild = Total_HuffmanNode[i]->rchild = NULL;  
    }  
  
    for (i=0; iweight < Total_HuffmanNode[FirstSmall]->weight)  
                {  
                    SecondSmall = FirstSmall;  
                    FirstSmall = j;  
                } else if (Total_HuffmanNode[j]->weight < Total_HuffmanNode[SecondSmall]->weight)  
                {  
                    SecondSmall = j;  
                }  
            }  
        }  
        hufmTree = (HuffmanNode*)malloc(sizeof(HuffmanNode));  
        hufmTree->weight = Total_HuffmanNode[FirstSmall]->weight + Total_HuffmanNode[SecondSmall]->weight;  
        hufmTree->lchild = Total_HuffmanNode[FirstSmall];  
        hufmTree->rchild = Total_HuffmanNode[SecondSmall];  
  
        Total_HuffmanNode[FirstSmall] = hufmTree;  
        Total_HuffmanNode[SecondSmall] = NULL;  
    }  
    free(Total_HuffmanNode);  
    return hufmTree;  
}  
  
// 打印哈夫曼树  
void PrintHuffmanTree(HuffmanNode* hufmTree)  
{  
    if (hufmTree)  
    {  
        printf("%d", hufmTree->weight);  
        if (hufmTree->lchild != NULL || hufmTree->rchild != NULL)  
        {  
            printf("(");  
            PrintHuffmanTree(hufmTree->lchild);  
            printf(",");  
            PrintHuffmanTree(hufmTree->rchild);  
            printf(")");  
        }  
    }  
}  
  
// 递归进行哈夫曼编码  
void HuffmanCode(HuffmanNode* hufmTree, int depth)      // depth是哈夫曼树的深度  
{  
    static int code[10];  
    if (hufmTree)  
    {  
        if (hufmTree->lchild==NULL && hufmTree->rchild==NULL)  
        {  
            printf("index为%d权值为%d的结点的哈夫曼编码 ", hufmTree->index, hufmTree->weight);  
            int i;  
            for (i=0; ilchild, depth+1);  
            code[depth] = 1;  
            HuffmanCode(hufmTree->rchild, depth+1);  
        }  
    }  
}  
  
// 哈夫曼解码  
void HuffmanDecode(char DecodeStr[], HuffmanNode* hufmTree, char NodeStr[])  // DecodeStr是要解码的01串，NodeStr是结点对应的字符  
{  
    int i;  
    int CodeNum[100];  
    HuffmanNode* Total_HuffmanNodeTree = NULL;  
    for (i=0; ilchild!=NULL && Total_HuffmanNodeTree->rchild!=NULL)  
            {  
                if (CodeNum[i] == 0)  
                {  
                    Total_HuffmanNodeTree = Total_HuffmanNodeTree->lchild;  
                } else  
                {  
                    Total_HuffmanNodeTree = Total_HuffmanNodeTree->rchild;  
                }  
                ++i;  
            }  
            printf("%c", NodeStr[Total_HuffmanNodeTree->index]);     // 输出解码后对应结点的字符  
        }  
    }  
}  

//mian.c 
#include   
#include   
#include   
#include "Huffman.h"  

int main()  
{  
    int i, n;  
    printf("请输入结点的个数：\n");  
    while(1)  
    {  
        scanf("%d", &n);  
        if (n>1)  
            break;  
        else  
            printf("错误，请重新输入n值！");  
    }  
  
    int* ArrLeafNode_Weight;  
    ArrLeafNode_Weight=(int*)malloc(n*sizeof(LeafNode));  
    printf("请输入%d个结点的权值：\n", n);  
    
    for (i=0; i