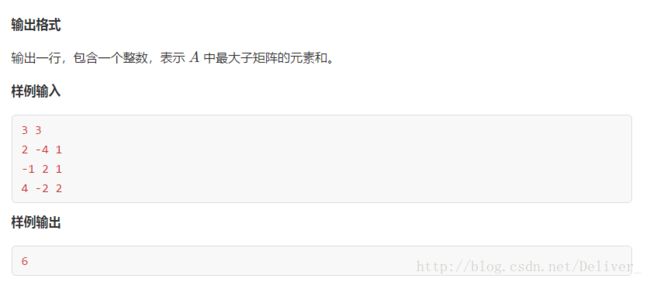
计蒜客 最大子阵

动态规划思想，先解决一维的最大子段和，然后这道题可以将二维降到一维来做的。

#include 
#include 

using namespace std;

int MaxSubArray(int a[], int n)
{
    int record[n];
    record[0] = a[0];
    for (int i = 1; i < n; i++)
        record[i] = record[i-1] + a[i];
    int max = record[0];
    for (int i = 1; i < n; i++)
    {
        if (record[i] > max)
                max = record[i];
        for (int j = 0; j < i; j++)
        {
            int sum = record[i] - record[j];
            if (sum > max)
                max = sum;
        }
    }
    return max;
}

int main()
{
    int a[55][55];
    int dp[55];
    int n, m;
    int max1, max2;
    cin >> n >> m;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cin >> a[i][j];
        }
    }
    max1 = -999999;
    for (int i = 0; i < n; i++)
    {
        memset(dp, 0, sizeof(dp));
        for (int j = i; j < n; j++)
        {
            for (int k = 0; k < m; k++)
            {
                dp[k] += a[j][k];
            }
            max2 = MaxSubArray(dp, m);
            if (max2 > max1)
                max1 = max2;
        }
    }
    cout << max1 << endl;
    return 0;
}