堆（heap）

堆（heap）

一、写在前面

   完全二叉树：若设二叉树的深度为h，出第h层外，其他各层（1~h-1）的节点数都达到最大个数，第h层所有的节点都连续集中在最左边。

   堆（heap）是一种数组对象，他可以被视为一颗完全二叉树结构。他的特点是父节点的值大于（小于）两个子节点的值（分别称为大堆和小堆）。他常用于管理算法执行过程中的信息，应用的场景包括堆排序、海量数据处理（TopK）问题和优先级队列等。

声明：本文虽以仿函数实现了大堆和小堆，但以大堆为例讲解。

二、堆得构建及其基本操作

   1、建堆

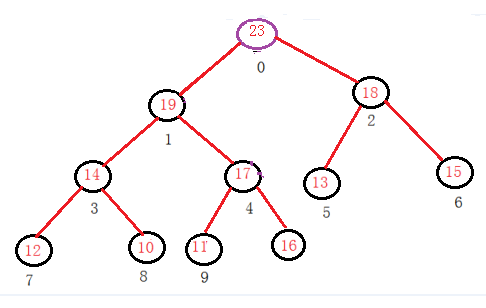
   如图所示，将数组想象为以下标0为树根（堆顶），左孩子下标等于父亲下标乘二加1，左孩子下标等于父亲下标乘二加2,的完全二叉树。

   方法详解：先利用vector创建一个数组，并将所有数据先放入数组中（push_back()）。之后用向下调成算法（_AdjustDown(parent)）将较小的数下沉，这样大的数则上升。其中parent为需要向下调整的数的下标，再定义一个child=parent*2+1为parent的左孩子。先判断parent的右孩子存不存在，如果存在，则比较左右孩子的数据谁大，右孩子大则child++。再将大的孩子与parent的数据相比，child大则将其数据与parent的数据互换。最后将child变为parent，child变为child左孩子继续向下调整。

   见下图

   

           2、插入数据

 

   3、删除数据（头删）

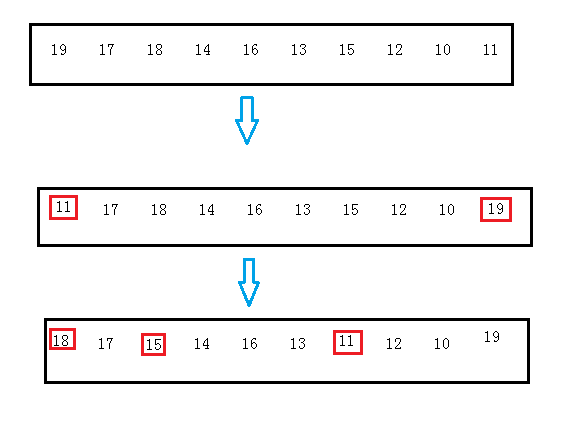
   头删即删除堆顶的数据，由于是堆结构，头删必定会破坏其稳定结构，所以需要调节。这里使用的方法是将堆顶数据与数组中最后一个数据交换，然后调用vector的pop_back()方法删除最后一个数据（即原堆顶数据），最后将堆顶的数据向下调整即可。

三、堆得应用

   1、堆排序（heap_sort，升序）

   这里还是利用的向下调整的算法，不过需要修改一点，那就是传的参数需要增加一个调整的范围size。堆排序前提是数组已经是一个堆得结构，然后我们将堆顶的数据与最后一个数据交换，最后一个数据不包含在范围里进行向下调整。

   2、海量数据处理（topK）

   假设有1000个数据需要选出最大的10个数。我们将这1000个数放入数组a中，并选出前10个数，复用之前的代码建立一个大小为10的小堆。再将数组a中剩下的数据依次与堆顶数据比较，如果比堆顶数据大，则两数交换，并且堆进行向下调整。这样比较完之后堆中必定留下的是最大的10个数。

下面是海量数据处理的代码：

void AdjustDown(int* heap, size_t parent, int k)
{
	size_t child = parent * 2 + 1;
	while (child < k)
	{
		if (child + 1 < k && heap[child + 1] < heap[child])
		{
			++child;
		}

		if (heap[child] < heap[parent])
		{
			swap(heap[child], heap[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
			break;
	}
}

void TopK(int* a, int n, int k)//海量数据处理
{
	assert(n > k);
	int* heap = new int[k];
	for (size_t i = 0; i < k; i++)
	{
		heap[i] = a[i];
	}

	for (int i = (k - 2) / 2; i >= 0; --i)
	{
		AdjustDown(heap, i, k);
	}

	for (int j = k; j < n; j++)
	{
		if (a[j] > heap[0])
		{
			swap(a[j], heap[0]);
			AdjustDown(heap, 0, k);
		}
	}

	for (int m = 0; m < k; m++)
	{
		cout << heap[m] << " ";
	}
	cout << endl;
	delete[] heap;
}

void test()                        //海量数据处理测试
{
	int a[1000];
	for (int i = 0; i < 1000; i++)
	{
		a[i] = i;
	}
	a[100] = 2000;
	a[0] = 1002;
	TopK(a, 1000, 10);
}

四、代码区

#pragma once

#include
#include
#include
using namespace std;


template
struct Less                                  //小堆
{
	bool operator()(const T& l, const T& r)
	{
		return l < r;
	}
};

template
struct Greater                               //大堆
{
	bool operator()(const T& l, const T& r)
	{
		return l > r;
	}
};

template
class Heap
{
public:
	Compare func;
	Heap(T* a, size_t n)//构造堆
	{
		_a.reserve(n);
		for (size_t i = 0; i < n; i++)
		{
			_a.push_back(a[i]);
		}
		for (int i = (_a.size() - 2) / 2; i >= 0; i--)
		{
			_AdjustDown(i);
		}
	}

	const T& Top() const//取堆顶
	{
		return _a[0];
	}

	void Push(const T& x)//插入一个数据
	{
		_a.push_back(x);
		_AdjustUp(_a.size() - 1);
	}

	void Pop()//删除数据
	{
		assert(_a.size() > 0);
		swap(_a[_a.size() - 1], _a[0]);
		_a.pop_back();
		_AdjustDown(0);
	}

	void Heap_Sort(T* a, int n)//堆排序（升序）
	{
		for (size_t i = n - 1; i > 0;--i)
		{
			swap(_a[0], _a[i]);
			_Adjust(0,i);
		}
	}


protected:
	void _Adjust(size_t parent, int size)//堆排序的向下调整
	{
		size_t child = parent * 2 + 1;
		while (child < size)
		{
			if (child + 1 < size && func(_a[child + 1], _a[child]))
			{
				++child;
			}

			if (func(_a[child], _a[parent]))
			{
				swap(_a[child], _a[parent]);
				parent = child;
				child = child * 2 + 1;
			}
			else
				break;
		}
	}

	void _AdjustUp(size_t child)//向上调整
	{
		size_t parent = (child - 1) >> 1;
		while (child > 0)
		{
			if (func(_a[child], _a[parent]))
			{
				swap(_a[child], _a[parent]);
				child = parent;
				parent = (child - 1) >> 1;
			}
			else
				break;
		}
	}

	void _AdjustDown(size_t parent)//向下调整
	{
		size_t child = parent * 2 + 1;
		while (child < _a.size())
		{
			if (child + 1 < _a.size() && func(_a[child + 1], _a[child]))
			{
				++child;
			}

			if (func(_a[child], _a[parent]))
			{
				swap(_a[child], _a[parent]);
				parent = child;
				child = child * 2 + 1;
			}
			else
				break;
		}
	}
protected:
	vector _a;
};

void Test()
{
	int a[10] = { 10, 16, 18, 12, 11, 13, 15, 17, 14, 19 };
	Heap> Hp((int*)a, 10);
	Hp.Push(23);
	Hp.Pop();
	Hp.Heap_Sort((int*)a, 10);
}