2017国庆 雅礼集训 题解合集
D1
D1 T1:Clique:
我做的题太少啦,这都没看出来。首先,这个式子是 c[i]−c[j]>=dis(i,j) ,即在数轴上这样的圆,如果没交点,那么就有边,所以就是最长区间不覆盖。
#includeD1 T2:Mod
好题啊!!要记下来。
套路题。首先,如果一个区间内最大的数都没有模数大,就不用模啦,因为这是无效的膜。又每次取模后,都只最多剩下以前的一半,所以在这个数不变的情况下,这个数最多有效的被模 logn 次,这个可以暴力修改。那么每个数被修改 logn 次,一次改是 logn 的,总的就是 nlognlogn 。
#includeD1 T3:Number
就是你会发现,随着n的变大,那段区间在二进制中有 k 个一的数不会减少。因为从 k 到 k+1 时,有 2k 在二进制中与 k 的 1 的个数相同,所以不会减少。那么就可以数位dp一下。令 S(i)=i+1,2,…,2i , f(i,k) 表示 S(i) 中二进制下恰好有 k 个 1 的数的个数 (i>0,k≥0) 。设为中有几个数 f(i,k)=Σmin(k,p)x=1Ck−x+1ax+1−Ck−x+1ax ,其中 p 表示 i 在二进制下1的个数, ax 表示 i在二进制下第x高的1所在位代表的2的幂次。特判掉 k≤1 ,那么所有满足条件的 n都在 2∗1018 以内。 用二分或逐位贪心求出最小和大的 n 即可。
#include D2
D2 T1 :Mine
神奇的定义与转移。设 f(i,j) 表示当前填第 i 个字符为 j 的方案数,即j表示当前这个位置还缺几个雷,如果是2就表示这个位置本身就是雷。然后 dp 就好搞啦。
#includeD2 T2:Water
就是水如果能流出去,那么一定有一条路径使得其路径上的值都小于其高度。如果流不出去,那么所有路径上的最大值的最小值要大于其高度(因为一条路径上水只会被最高的挡住,而木桶原理,水只会在最低的被挡住的高度被留住)。所以问题就是从这个块走出矩形的所有路径上的最大值的最小值。相邻块连边,权值为两块的较大值,矩形边界的块向“矩形外”连边,权值为 max(高度,0) ,做最小生成树。(最短路也可以)
#include1]);
addedge(idx(i,j),idx(i,j+1),value);
}
for (ll i=1;ifor (ll j=1;j<=m;j++)
{
value = max(mat[i][j] , mat[i+1][j]);
addedge(idx(i,j),idx(i+1,j),value);
}
for (ll i=2;i<=n-1;i++)
{
addedge(0 , idx(i,1) , max(mat[i][1] , (ll)0 ) );
addedge(0 , idx(i,m) , max(mat[i][m] , (ll)0 ) );
}
for (ll j=1;j<=m;j++) addedge(0,j,max((ll)0,mat[1][j]));
for (ll j=1;j<=m;j++) addedge(0 , idx(n,j) , max((ll)0,mat[n][j]));
SPFA(0);
for (ll i=1;i<=n;i++)
{
for (ll j=1;j<=m;j++)
{
if (dis[idx(i,j)] <= mat[i][j]) printf("0 ");
else printf("%lld ",dis[idx(i,j)]-mat[i][j]);
//printf("%lld ",dis[idx(i,j)]);
}
putchar('\n');
}
//for (ll i=1;i<=m*n;i++)
//printf("%d ",dis[i]);
return 0;
}
D2 T3:Gcd:
乱反演一下,然后那个桶记因数出现次数。用 f(i) 表示gcd为i的数对个数, g(i) 表示gcd为i的倍数的数对个数。那么 f(i)=Σμ(d)g(d) ,我们只需要维护 g(1) g(max(xi)) 。记s(i)表示i的倍数的个数,那么 g(i)=s(i)∗(s(i)−1)/2 ,我们只需要在加入/删除一个数时枚举它的因数修改s即可。
#includeD3
D3 T1:string
就是对每种字母单独造棵线段树,然后合并。有点神。
#include1);
for(i=1;i<2*p;i++)
g[i]=-1;
for(i=1;i<=n;i++)
change(1,1,p,i,i,s[i-1]-'a');
while(m--)
{
scanf("%d%d%d",&i,&j,&k);
x=sum(1,1,p,i,j);
if(k)
for(k=0;k<26;k++)
{
if(x.a[k])
change(1,1,p,i,i+x.a[k]-1,k);
i+=x.a[k];
}
else
for(k=25;k>=0;k--)
{
if(x.a[k])
change(1,1,p,i,i+x.a[k]-1,k);
i+=x.a[k];
}
}
for(i=1;i1);
for(i=1;i<=n;i++)
printf("%c",'a'+g[p+i-1]);
printf("\n");
return 0;
} D3 T2:Matrix
这道题只好意会一下,用 f[i][j] 表示做到前 i列,已经有 j列在右侧区间放 1的方案数。 i 越过一个左侧区间的右端点时,从之前剩下空列中选一个在这个左侧区间放 1。也就是说,在扫到i时,我们只在右端点不大于i的左区间放1,转移时分在右侧区间放1或不放 1。还是好转移的。
#includeD3 T3:Big
我们发现,对手是把我们现在得到的数在二进制下把第一位移到最右边(位数限制为 n 位的二进制数),又因为我们可以取遍1到 2n−1 的数,所以换不换没啥意义,就是要把a序列换一下。问题转化为选一个数,使它左移位后与 m+1 个给定数分别异或的最小值大。然后造字典树,如果当前为0,1都有,则出来只能是0,反之只有一个,则是1。
#includeD4
D4 T1:Mayuri
就是约瑟夫问题,可以有 O(min(n,m)) 或 O(mlogn) 的,又因为m小,所以用第一个好一点。
#includeelse{p+=m*(n-i);i=n;}
}
return p%n;
}
D4 T2:Kurisu
化简之后变成这个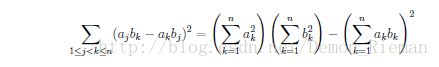
然后bit就好啦。
#includeD4 T3:Okarin
就是一个最长公共上升子序列。
(无输出方案版)
#includeD5
D5 T1:Adore
就是数位dp,0表示这位是偶数,1表示这位是奇数。
#includeD5 T2:Confess
乱搞,随机选n对就好啦(我绝对不会告诉你,倒着搜就不用随机啦)。证明:证明?我们不妨算一算如果随机选两个集合,他们交的期望 min(Σ2ni=1C(ci,2)C(n+1,2)|Σ2ni=1ci=n(n+1))=n−12 注意n 是偶数,所以大于 n−12 即可能会有交为n 的,由于大了一个常数,所以至少有 n 对!随机 O(n) 对即可。
这是STD,我的是倒着搜的,要遭hack,就不放啦。
#include D5 T3:Repulsed
就是贪心一样的 dp ,我们只配那些距离为k的房间与灭火器。考虑自底向上贪心。 G[x][k] 表示 x 下面距离为 k 的需要灭火器的房间数, F[x][k] 表示 x 下面距离为 k 的多余灭火器数,每个灭火器和房间的匹配在 lca 处理每次假设子树里已经最优了,那么 G[x][k] 一定要用 F[x][0] 填满。
#include
#include
using namespace std;
const int size = 100005;
typedef long long ll;
ll n,s,k;
ll ans = 0;
struct EDGE{
ll to,next;
}edge[ 2 * size];ll cnt=0;
ll fa[size] , head[size];
ll f[size][30],g[size][30];
void adde(ll fr,ll to)
{
edge[++cnt]=(EDGE){to,head[fr]};
head[fr] = cnt;
}
void addedge(ll fr,ll to)
{
adde(fr,to);
adde(to,fr);
}
ll calc(ll x) {return (x/s + ( ( x % s ) > 0 ) ); }
ll dfs1(ll node,ll Fe)
{
fa[node] = Fe;
for (ll j =head[node];j;j = edge[j].next)
if (edge[j].to!= Fe) dfs1(edge[j].to,node);
}
ll dfs2(ll node)
{
for (ll j=head[node];j;j=edge[j].next)
{
if (edge[j].to!=fa[node])
{
dfs2(edge[j].to);
for (ll i = 1;i <= k;i++)
{
f[node][i] = min(n , f[node][i] + f[edge[j].to][i-1]);
g[node][i] += g[edge[j].to][i-1];
}
}
}
g[node][0]++;
if (g[node][k])
{
ll need = calc(g[node][k]);
ans += need;
f[node][0] = min (need * s , n);
}
for (ll i=0;i<=k;i++)
{
ll j = min(g[node][i],f[node][k-i]);
g[node][i] -= j; f[node][k-i] -= j;
}
for (ll i=0;i<=k-1;i++)
{
ll j = min(g[node][i],f[node][k-1-i]);
g[node][i] -= j; f[node][k-1-i] -= j;
}
}
int main()
{
scanf("%lld%lld%lld",&n,&s,&k);
for (ll i=1;ito;
scanf("%lld%lld",&fr,&to);
addedge(fr,to);
}
dfs1(1,0);
dfs2(1);
for (ll i=0;i<=k;i++)
for (ll j=0;j<=k;j++)
{
if (i+j<=k)
{
ll need = min(f[1][i],g[1][j]);
f[1][i] -= need; g[1][j] -= need;
}
}
ll cnt=0;
for (ll i=0;i<=k;i++) cnt+=g[1][i];
ans += calc(cnt);
printf("%lld",ans);
}
D6
D6 T1:starway
好题。你考虑如果现在我们定一个答案,那么我们人就可以变成一个园啦,如果走不动,那么拦住他的就是一条路径,那么每个点再与上下边界连表,就变成了最小生成树。这是完全图,用 prim ,然后边存不下,就可以先不存,扫的时候在算,然后更新后才加边。这样还不用打标记,造好了图直接跑就可以啦。
//看我程序多美观
//美观啊,太美观了!!!
#include D6 T2:knows
其实就是极长上升序列考虑 O(n2) 的 dp , fi 表示左边最后一个选的是谁,每次转移的时候枚举一个前面既不相交,又能保证极长的 j 转移这样的j一定是个上升序列,线段树维护上升序列即可。复杂度为 O(nlog2n) 。
#include D6 T3:lost
维护凸包,二分弹栈。
#includeD7
D7 T1 :conjucate
期望可加性,考虑每个在第一个数之前被抓的概率,并且与其他元素无关,有独立性,所以有第i堆的贡献是: aiai+a1 。
#includeD7 T2:conjuct
乱搞dp lcs。
//做不来啦、、、粘的STD
#include D7 T3:conjecture
乱搞。
D8
D8 T1 graph:
贪心,把图建成树,然后每次贪心取,注意到我们应该在这个点的边数为偶数时全取,奇数时向下再取一个。
#includeD8 T2 permutation:
注意到我们先反一下原数列,构造 p[i] 表示i现在在原来的那个数列,所以现在交换就变成了相邻交换。然后有些距离小于 k 的两个的相对位置不会变,所以靠此建图,拓扑排序,dfs一遍就好了。
#includepos[j]-ibreak;
if(!fl)fl=1;
swap(pos[a[i]],pos[j]);
swap(a[pos[a[i]]],a[pos[j]]);
}
}
}
for(int i=1;i<=n;++i)printf("%d\n",a[i]);
}
else
{int i,x;
for (i=1;i<=n;i++)
read(p[i]),q[p[i]]=i;
SegTree::init();
for (i=n;i>=1;i--)
{
x=SegTree::query(1,1,n,q[i]-k+1,q[i]);
if (x<=n) addedge(q[x],q[i]);
x=SegTree::query(1,1,n,q[i],q[i]+k-1);
if (x<=n) addedge(q[x],q[i]);
SegTree::update(1,1,n,q[i],i);
}
for (i=1;i<=n;i++)
if (!deg[i]) pq.push(i);
for (i=n;i>=1;i--)
{
int u=p[i]=pq.top(); pq.pop();
for (int p=FIR[u];p;p=NEXT[p])
if (!(--deg[TO[p]])) pq.push(TO[p]);
}
for (i=1;i<=n;i++) q[p[i]]=i;
for (i=1;i<=n;i++) printf("%d\n",q[i]);
}
}
D8 T3 tree:
每条边都至少出现了一次,所以最优的情况就是所有边权之和,然后能不能取到证不来,反正可以,所以加起来就好啦。(注意爆longlong)
#includescanf("%lld%lld%lld",&fr,&to,&val) ,ans+=val;
printf("%lld",ans);
return 0;
} 总结:
这次去雅礼,总的考的不好,也许是因为是高一不稳定的原因。所以回来后要好好提升自己的知识水平,下次去AK雅礼集训。