Chapter 9 On-policy Prediction with Approximation
本文为《Reinforcement Learning: An Introduction》读书笔记
-
- 9.1 Value-function Approximation
- 9.2 The Prediction Objective ( VE¯¯¯¯¯¯¯¯ V E ¯ )
- 9.3 Stochastic-gradient and Semi-gradient Methods
- 9.4 Linear Methods
- 9.5 Feature Construction for Linear Methods
- 9.5.1 Polynomials
- 9.5.2 Fourier Basis
- 9.5.3 Coarse Coding
- 9.5.4 Tile Coding
- 9.5.5 Radial Basis Functions
- 9.6 Selecting Step-Size Parameters Manually
- 9.7 Nonlinear Function Approximation: Arti cial Neural Networks
- 9.8 Least-Squares TD
- 9.9 Memory-based Function Approximation
- 9.10 Kernel-based Function Approximation
- 9.11 Looking Deeper at On-policy Learning: Interest and Emphasis
- 总结
之前学习的方法都是基于表格的方法,现在要用approximation来替换表格。
本书后面的两个重点:
1. update target
2. updte distribution
9.1 Value-function Approximation
Machine learning methods that learn to mimic input-output examples in this way are called supervised learning methods, and when the outputs are numbers, like u, the process is often called function approximation
正因为学习approximation function的过程是监督学习过程,所以介意使用任意函数来做监督学习,比如神经网络。
9.2 The Prediction Objective ( VE¯¯¯¯¯¯¯¯ V E ¯ )
Mean Squared Value Error,即 VE¯¯¯¯¯¯¯¯ V E ¯
其中 v^(s,w) v ^ ( s , w ) 为 approximate value; vπ(s) v π ( s ) 为true value; μ(s) μ ( s ) 表示处于状态s的时间百分比,在 on-policy training中 μ(s) μ ( s ) 被称为 on-policy distribution
这也是本章要讲的内容

对于连续任务, on-policy distribution就是在 π π 下的状态分布。
9.3 Stochastic-gradient and Semi-gradient Methods
在梯度下降方法中,使用权重向量 w≐(w1,w2,⋯,wd)T w ≐ ( w 1 , w 2 , ⋯ , w d ) T ,来approximate value function v^(s,w) v ^ ( s , w )
Stochastic gradient-descent (SGD)
因为 vπ(s) v π ( s ) 并不是已知的,我们使用 unbiased estimate Ut U t 来代替它。
在蒙特卡洛方法中, Ut U t 是可以计算出来的, Ut≐Gt U t ≐ G t ,所以梯度下降版本的蒙特卡洛 state-value prediction 保证能找到局部最优

如果使用 Bootstrapping 就不会得到这样的保证。
Bootstrapping将不会产生真正的梯度下降方法,原因是targets,如n-step returns Gt:t+n G t : t + n 或DP target ∑a,s′,rπ(a|St)p(s′,r|St,a)[r+γv^(s′,wt)] ∑ a , s ′ , r π ( a | S t ) p ( s ′ , r | S t , a ) [ r + γ v ^ ( s ′ , w t ) ] 都依赖于权重向量 wt w t 的当前值,这表示target将是有偏的,所以不会产生真正的梯度下降方法。
上面说到的这种方法,因此被称为 semi-gradient methods
虽然不保证收敛,但是使用Semi-gradient可以显著提高学习速度,而且允许连续和在线学习
Semi-gradient TD(0),使用 Ut≐Rt+1+γv^(St+1,wt) U t ≐ R t + 1 + γ v ^ ( S t + 1 , w t )

State aggregation
状态聚合是一种简单形式的广义函数逼近,其中状态被分组在一起,每个组具有一个估计值(权重向量w的一个分量)。
状态聚类是一种特殊的SGD,这里每个state group的梯度都等于1。
9.4 Linear Methods
使用线性函数作为 approximation function,来逼近 v^(s,w) v ^ ( s , w ) 。其中 x(s) x ( s ) 被称为 feature vector,用来表示状态s
SGD
semi-gradient TD(0)
当更新达到稳定的时候,可以得到
其中
对于上式,因为已经达到稳定状态,所以必然收敛到权重向量 wTD w T D
linear semi-gradient TD(0) 被证明是收敛到 TD fixed point的,书上有详细证明。而且在 TD fiexed point,在连续的情形下 VE¯¯¯¯¯¯¯¯ V E ¯ 被证明是在可能的最低误差的有限扩展范围内
One-step semi-gradient action-value 方法,如 semi-gradient Sarsa(0)也收敛于类似的fixed point和类似的bound。
对于其他更新分布,使用function approximation的bootstrapping方法实际上可能会发散到无穷大。
9.5 Feature Construction for Linear Methods
A limitation of the linear form is that it cannot take into account any interactions between features, such as the presence of feature i being good only in the absence of feature j.
9.5.1 Polynomials
使用多项式 逼近
把上面的两个变量扩展到 k 个,则
这些特征构成了n阶k维多项式,包含 (n+1)k ( n + 1 ) k 个不同的特征
9.5.2 Fourier Basis
其中 ci=(ci1,⋯,cik) c i = ( c 1 i , ⋯ , c k i ) , 有 cij∈0,⋯,n c j i ∈ 0 , ⋯ , n for j=1,⋯,k j = 1 , ⋯ , k and i=0,⋯,(n+1)k i = 0 , ⋯ , ( n + 1 ) k
9.5.3 Coarse Coding
粗糙编码。表示有重叠的特征的状态。对每个训练状态,包含这个状态的所有圆相当于是特征的权重,区别在在于它们的重叠
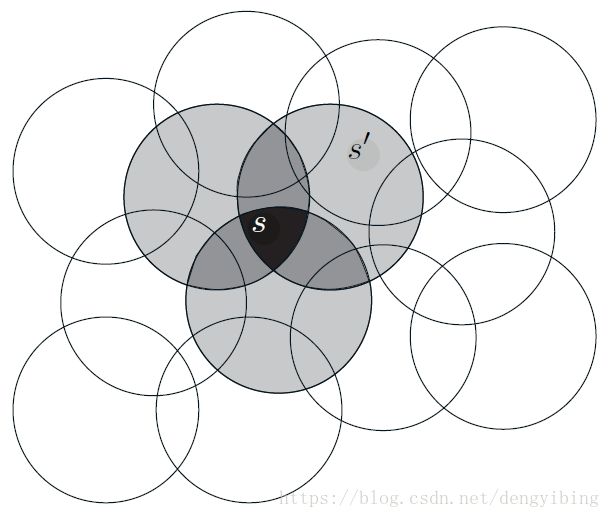
用圆来代表特征,一个状态(落到其中的某个点)与很多圆相交,就受到这么多状态的影响。学习的时候也会影响该点所涉及的所有状态
9.5.4 Tile Coding
如下图所示,每个这样的划分被称为 tiling,每个划分中的元素被称为 tile。
在只有一个tiling的时候只有利用了state aggregation,只有使用multiple tiling才能使用到Coarse Coding的优势。从下图看出,每个tiling都有一个偏移。这里通常设置step-size为 α=1/n α = 1 / n
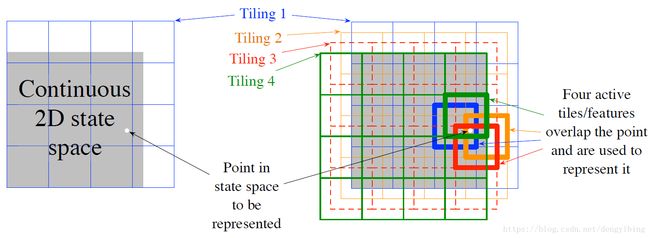
但是有个问题,当所有的offset都是一样的时候会有artifact产生,所以可以使用非对称的偏移来避免这个问题。w表示tile width,n表示tilings的数量,w/n表示基本单元。
In particular, for a continuous space of dimension k, a good choice is to use the first odd integers (1,3,5,7,…,2k-1), with n (the number of tilings) set to an integer power of 2 greater than or equal to 4k.
9.5.5 Radial Basis Functions
Radial basis functions (RBFs)
9.6 Selecting Step-Size Parameters Manually
A good rule of thumb for setting the step-size parameter of linear SGD methods is then
9.7 Nonlinear Function Approximation: Arti cial Neural Networks
使用神经网络来做函数逼近
9.8 Least-Squares TD
上面降到的方法都是迭代法,现在用代数的方式一次算出结果。而且LSTD的数据利用率高
计算出A和b,然后一次性计算出 wt w t 。跟上面讲的TD(0)一样有fixed point
Least-Squares TD algorithm
最终有
但是LSTD的计算复杂性很高,这里A在最后计算的时候是要求逆的,需要时间复杂度是 O(d3) O ( d 3 ) ,但是这里对A的计算是外积加和形式,所以可以写成增量更新的形式,计算复杂度变成了 O(d2) O ( d 2 )

all with only O(d2) O ( d 2 ) memory and per-step computation
9.9 Memory-based Function Approximation
非参数化方法。把训练样本保存在内存中。当有查询需求的时候,取出一组样本用来计算查询状态的估计值。也称作lazy learning。这里主要说local-learning,只使用查询状态的邻居来估计查询状态的值。其中有nearest neighbor method;weighted average methods;locally weighted regression。主要的好处是不受预先定义的函数形式的约束。主要的问题是加速最近邻居的查询,可以使用 k-d tree来加速。
9.10 Kernel-based Function Approximation
kernel function根据memory中状态与查询状态的距离,给予状态不同的权重。核方法还是Memory-based methods。
Kernel regression
D is the set of stored examples
g(s’) denotes the target for state s’ in a stored example
线性参数回归方法也可以被看做是核方法,只不过使用的是线性核函数
“kernel trick”:它允许在扩展特征的高维空间中有效地工作,而实际上仅使用一组存储的训练示例。
9.11 Looking Deeper at On-policy Learning: Interest and Emphasis
现在的算法对于遇到的所有状态都给予相同的重视程度。但事实上,我们会更加重视某些states。即对不同的feature有不同的关注度。
interest It I t :非负的随机变量,表示在时刻t我们对准确估计状态的感兴趣的程度
Emphasis Mt M t :用来强调和弱化t时刻的学习
The general n-step learning rule
总结
Semi-gradient TD methods are not true gradient methods.


