title: 最大权闭合子图
date: 2018-12-15 17:47:40
tags:
- acm
- 刷题
categories: ACM-网络流-最大权闭合子图
https://www.cnblogs.com/31415926535x/p/10124530.html
概述
某一天在翻cf上的contest时,,发现最近的某一场的G题是网络流的题,,,正好最近看了看网络流的题,,想着把他弄出来,,,然后查了一下发现是网络流里最大权闭合子图的问题,,于是就一直拖到现在才基本弄懂。。。。最大权闭合子图的解法很简单,,,其中一部分的计算利用到了求解网络的最大流的那几个算法,,主要是理解它的性质和建图,,,,
题目分析
首先是cf的那道题,,,传送门,,,
题目的意思
大致意思是他定义了一个网络的子图是子图中的点的后继节点也在子图中,,(后继节点就是指1->2->3 , 2就是1的后继节点,,3就是2的后继节点),,然后要你找出最大的子图的权,,,,
题目的描述的其实就是闭合子图的性质,,,所问其实也就是最大权闭合子图,,,
接下来是有关最大权闭合子图的一些概念
最大权闭合子图
以下资料引用自这里
还有这里,,,
(本文所引用内容版权归原作者所有)
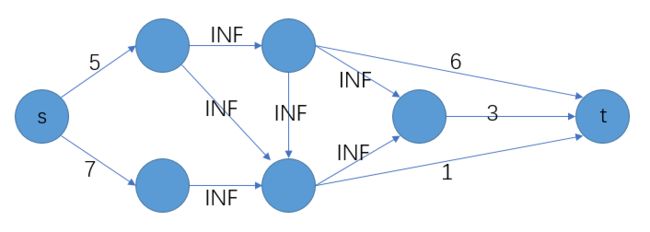
首先对于一个有点权的有向连通图:
用超级源点s和超级汇点t将正权值的点连到s负权值的连到t上,,这样可以将点权图转化为一个边权图,,,:
结论
- 该带边权的有向图的s-t最小割是简单割,,(简单割就是割集中的所有点都与s或t相连),,所以最小割不会出现在inf的边上,,这样的图也是二分图,,,(这里看不懂了,,不过不影响,,)
- 该图中每一个简单割产生的两个子图中,含有s的子图是闭合图
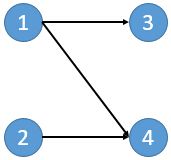
闭合图:在一个图中,选取一些点构成集合,若集合中的任一点连接点的任意出弧,其指向的点也在集合中,,,则这个集合构成的图就是闭合图,,
例如:
这个图的闭合子图就有8个:\(∅,\{3\},\{4\},\{2,4\},\{3,4\},\{1,3,4\},\{2,3,4\},\{1,2,3,4\}\)
- 最小割产生的子图s,t,图s是最大权闭合子图
证明如下:
因为割集中所有的边,不是连接在s上,就是连接在t上;
我们记割集中,所有连接在s上的边的权值和为\(x_1\),所有连接在t上的边的权值和为\(x_2\),而割集中所有边权值和为\(X=x_1+x_2;\)
又,记图S中所有点的权值和为\(W\),记其中正权值之和为\(w_1\),负权值之和为\(-w_2\),故\(W = w_1 - w_2;\)
而 \(W + X = w_1 - w_2 + x_1 + x_2\),由于\(x_2 = w_2\)(因为图S中所有负权值的点,必然连接到t点,而图S必然要与t分割开;故割集中,“连接在t点上的边权值和”就是“图S中所有负权值点的权值之和,取负”)
因而\(W + X = w_1 + x_1;\)
而显然的,\(w_1 + x_1\)是整个图中所有正权值之和,记为\(SUM\);
故\(W = SUM - X\),即 “图S中所有点的权值和” = “整个图中所有正权值之和” - “割集中所有边权值和”;
然后,因为\(SUM\)为定值,只要我们取最小割,则“图S中所有点的权值和”就是最大的,即此时图S为图S为最大权闭合子图;
总结
根据以上的论述,我们就可以得到求解一般的最大权闭合子图的步(tao)骤(lu):
- 记录图中的所有点权为正的和:\(sum\)
- 然后建图,建图的大概流程是:正点权的点与源点s相连,边权为点权,,负点权的点与汇点t相连,,边权为点权的相反数,,最后正负点之间相连,,边权为\(inf\)
- 最后跑网络路的最大流得到最大流\(maxflow\),,,最大权闭合子图的权值就是:\(sum - maxflow\)
有了这些,,这道板子题其实也就差不多了,,,和求最大流的不同只有建图和最后的处理了,,,
代码
//codefroces1082G
//https://codeforces.com/contest/1082/submission/47022828
//#include
#include
#include
#include
#include
#define aaa cout<<233< edge[stck[i]].cap - edge[stck[i]].flow)
{
mi = edge[stck[i]].cap - edge[stck[i]].flow;
inser = i;
}
}
for(int i = 0; i < top; ++i)
{
edge[stck[i]].flow += mi;
edge[stck[i] ^ 1].flow -= mi;
}//cout << mi << " ---" << inf << endl;
ans += mi;
top = inser;
u = edge[stck[top] ^ 1].to;
continue;
}
bool flag = false;
int v;
for(int i = cur[u]; ~i; i = edge[i].next)
{
v = edge[i].to;
if(edge[i].cap - edge[i].flow && dep[v] + 1 == dep[u])
{
flag = true;
cur[u] = i;
break;
}
}
if(flag)
{
stck[top++] = cur[u];
u = v;
continue;
}
int mi = n;
for(int i = head[u]; ~i; i = edge[i].next)
{
if(edge[i].cap - edge[i].flow && dep[edge[i].to] < mi)
{
mi = dep[edge[i].to];
cur[u] = i;
}
}
--gap[dep[u]];
if(!gap[dep[u]])return ans;
dep[u] = mi + 1;
++gap[dep[u]];
if(u != s)u = edge[stck[--top] ^ 1].to;
}
return ans;
}
int main()
{
// freopen("233.txt" , "r" , stdin);
// freopen("233.out" , "w" , stdout);
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
init();
cin >> n >> m;
int x;
int s = 0;int t = n + m + 1;
for(int i = 1; i <= n; ++i)
{
cin >> x;
addedge(i , t , x);
}
int u , v , w;
ll ans = 0;
for(int i = 1; i <= m; ++i)
{
cin >> u >> v >> w;
addedge(n + i , u , inf);
addedge(n + i , v , inf);
addedge(s , n + i , w);
ans += w;
}
ans -= isap(s , t , n + m + 2);
cout << ans << endl;
return 0;
} 之后又找了一道这样的题,,,还是在建图上做文章,,,就是和上一道一样的敲错了板子,,,死活运行不正确,emmmmm,,,还有初始化函数init()总是忘记调用,,,菜的流泪,,,,QAQ
题目链接
题目大概意思是一个班的人选理科满意度加多少多少,,选文科加多少多少,,如果一个人的前后左右选的和他一样也加多少多少,,问你最大的满意值是多少,,,
思路是给这n*m个点和s点连的边权是文科的那个值,,和t点连的边权是理科那个值,,然后加一个新的点cnt,,和s点连,,边权为第三组满意度,,和其对应的相邻同学连inf的边,,选理科也就是和t连的新点同理,,最后跑网络流就行,,要求的满意值就是总的满意值-最小割的
//记得边数开大点,,貌似能有点数的30倍左右,,,之前re了一发QAQ
//https://www.luogu.org/problemnew/show/P4313
//https://www.luogu.org/record/show?rid=14708566
#include
#include
#include
#include
#define aaa cout<<233< edge[stck[i]].cap - edge[stck[i]].flow)
{
mi = edge[stck[i]].cap - edge[stck[i]].flow;
inser = i;
}
}
for(int i = 0; i < top; ++i)
{
edge[stck[i]].flow += mi;
edge[stck[i] ^ 1].flow -= mi;
}
ans += mi;
top = inser;
u = edge[stck[top] ^ 1].to;
continue;
}
bool flag = false;
int v;
for(int i = cur[u]; ~i; i = edge[i].next)
{
v = edge[i].to;
if(edge[i].cap - edge[i].flow && dep[v] + 1 == dep[u])
{
flag = true;
cur[u] = i;
break;
}
}
if(flag)
{
stck[top++] = cur[u];
u = v;
continue;
}
int mi = n;
for(int i = head[u]; ~i; i = edge[i].next)
{
if(edge[i].cap - edge[i].flow && dep[edge[i].to] < mi)
{
mi = dep[edge[i].to];
cur[u] = i;
}
}
--gap[dep[u]];
if(!gap[dep[u]])return ans;
dep[u] = mi + 1;
++gap[dep[u]];
if(u != s)u = edge[stck[--top] ^ 1].to;
}
return ans;
}
int m;
int getid(int i , int j)
{
return (i - 1) * m + j;
}
int main()
{
//freopen("233.txt", "r" , stdin);
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int n;
cin >> n >> m;
int u , v , w;
int s = 0;
int t = n * m + 1;
int sum = 0;
init();
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
cin >> w;
sum += w;
u = s;
v = getid(i , j);
addedge(u , v , w);
}
}
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
cin >> w;
sum += w;
u = getid(i , j);
v = t;
addedge(u , v , w);
}
}
int cnt = n * m + 1;//额外的点
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
cin >> w;
sum += w;
v = getid(i , j);
++cnt;
addedge(s , cnt , w);
addedge(cnt , v , inf);
for(int k = 1; k <= 4; ++k)
if(i + dx[k] >= 1 && i + dx[k] <= n && j + dy[k] >= 1 && j + dy[k] <= m)
addedge(cnt , getid(i + dx[k] , j + dy[k]) , inf);
}
}
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
cin >> w;
sum += w;
u = getid(i , j);
++cnt;
addedge(cnt , t , w);
addedge(u , cnt , inf);
for(int k = 1; k <= 4; ++k)
if(i + dx[k] >= 1 && i + dx[k] <= n && j + dy[k] >= 1 && j + dy[k] <= m)
addedge(getid(i + dx[k] , j + dy[k]) , cnt , inf);
}
}
cout << sum - isap(s , t , cnt + 1) << endl;
return 0;
}
剑之所指,心之所向,身之所往!!
(end)