杭电多校 Werewolf(狼人杀,并查集+思维)

Werewolf

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 677    Accepted Submission(s): 159

 

Problem Description

"The Werewolves" is a popular card game among young people.In the basic game, there are 2 different groups: the werewolves and the villagers.

Each player will debate a player they think is a werewolf or not. 

Their words are like "Player x is a werewolf." or "Player x is a villager.".

What we know is :

1. Villager won't lie.

2. Werewolf may lie. 

Of cause we only consider those situations which obey the two rules above. 

It is guaranteed that input data exist at least one situation which obey the two rules above.

Now we can judge every player into 3 types :

1. A player which can only be villager among all situations, 

2. A player which can only be werewolf among all situations.

3. A player which can be villager among some situations, while can be werewolf in others situations.

You just need to print out the number of type-1 players and the number of type-2 players. 

No player will talk about himself.

 

 

Input

The first line of the input gives the number of test cases T.Then T test cases follow.

The first line of each test case contains an integer N,indicating the number of players.

Then follows N lines,i-th line contains an integer x and a string S,indicating the i-th players tell you,"Player x is a S."

limits:

1≤T≤10

1≤N≤100,000

1≤x≤N

S∈ {"villager"."werewolf"}

 

 

Output

For each test case,print the number of type-1 players and the number of type-2 players in one line, separated by white space.

 

 

Sample Input

1

2

2 werewolf

1 werewolf

 

 

Sample Output

0 0

 

 

Source

2018 Multi-University Training Contest 6

 

 

Recommend

chendu   |   We have carefully selected several similar problems for you:  6373 6372 6371 6370 6369 

 

 

Statistic | Submit | Discuss | Note

【题意】:一群人玩狼人杀，只有两种角色，平民和狼人，已知每个人说‘一句话’，xx是xx，已知平民一定说真话，狼人不一定说真话还是假话，在所有情况下，一定是狼人的人有多少？一定是平民的人有多少？

【题解】:首先我们要读懂这道题 许多人可能都对这道题意有什么误解。我们输出的是所有情况下都”一定是狼人“的人的数量，必须能够明确指出几号是狼人，而不是至少有多少个狼人（不能确定是谁） 

所有情况下，所有人都是狼人一定都能推的过去，因此没有人一定是平民，这个好想，然后我们需要想的是一定是狼人的人。

我们要想证明一个人一定是狼人，可以用反证法，假设这个人是平民，然后发现与事实不成立，就可以说明这个人是狼人。

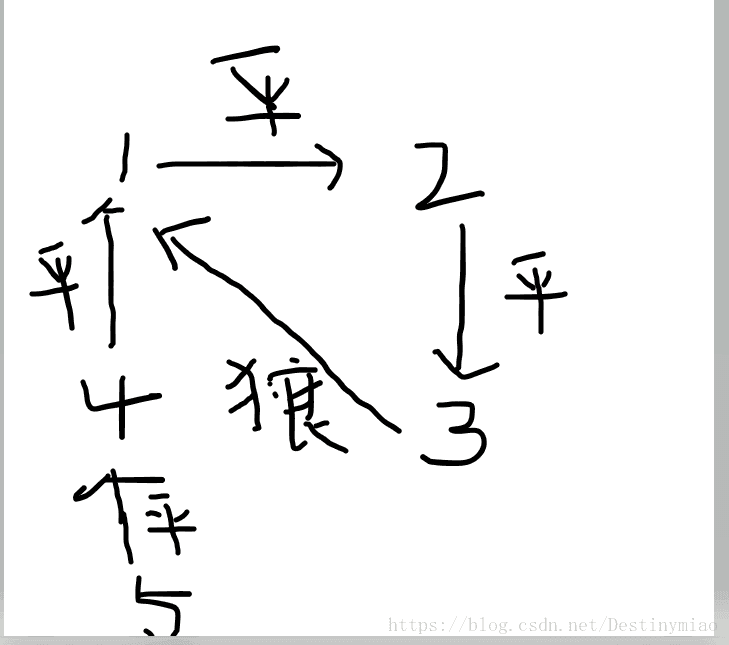
就是下图这种情况：

 

请忽略我画的图太丑了，，，能讲清楚就好 （捂脸）

我们假设1号玩家是平民 ，他说2号玩家是平民，（平民只会说真话），2号玩家说三号玩家是平民，则3号玩家说的话也一定是真话，但是3号玩家说1是狼人，于是推翻了我们的假设，1号玩家一定是狼人。 4号玩家说了谎，也一定是狼人，5号玩家也说了谎，也一定是狼人。 这张图就包含了一个人一定是狼人的所有情况，你们可以画画看。当一个人说的话能够反驳他自己，他就是狼人。

做法：我是用了两个并查集，第一个并查集是找出来一定是狼人的人，即上图中的一号，对所有的平民边建边，如果祖先节点发出了一条狼人边且指向并查集内部的人，则被指的这个人一定是狼人。先把所有这种狼人找出来，存到一个集合中。

2、处理小尾巴，即4，5. 如果一个人对一个已经确定是狼人的人发出平民边，则这个人也是狼人。第二个并查集合并有两种情况：一是两个不能确定身份的且通过平民边连接的玩家，另一个是不能确定身份的人向已经确定是狼人的人发出平民边。合并这两种情况，用一个数组统计一下并查集中元素的个数。

【代码】

#include
using namespace std;
const int maxn=1e5+3;
int pre[maxn];
int wolf[maxn];
int vis[maxn];
int cnt[maxn];//记录并查集中元素的数量
struct player
{
    int id;
    char c;
}info[maxn];
int find(int x)
{
    if(x!=pre[x])
        pre[x]=find(pre[x]);
    return pre[x];
}
void joint(int x,int y)
{
    int fx=find(x),fy=find(y);
    if(fx!=fy)
        {
            pre[fx]=fy;
            cnt[fy]+=cnt[fx];
        }
}
 
int main()
{
    int T,n;
    cin>>T;
    while(T--)
    {
        cin>>n;
        memset(wolf,0,sizeof(wolf));
        memset(vis,0,sizeof(vis));
        memset(cnt,1,sizeof(cnt));
        for(int i=1;i<=n;i++)
            pre[i]=i;
        for(int i=1;i<=n;i++)
        {
            int num;
            char s[10];
            cin>>num>>s;
            info[i].id=num;
            info[i].c=s[0];
            if(s[0]=='v')
                joint(i,num);
        }
        for(int i=1;i<=n;i++)
        {
            int f=find(i);
            if(vis[f]==0&&info[f].c=='w')
            {
                vis[f]=1;
                int p=info[f].id;
                if(find(p)==f)
                    wolf[p]=1;//玩家p是狼
            }
        }
        for(int i=1;i<=n;i++)
            pre[i]=i;
        memset(vis,0,sizeof(vis));
 
        for(int i=1;i<=n;i++)
            cnt[i]=1;
 
        for (int i=1;i<=n;i++)
        {
            if(wolf[i]==0)
            {
                int v=info[i].id;
                char s=info[i].c;
                if(wolf[v]==0&&s=='v')
                    {
                        joint(i,v);
                    //printf("1  i=%d,v=%d\n",i,v);
                    }
                else if(wolf[v]==1&&s=='v')
                    {
                        joint(i,v);
                   // printf("2  i=%d,v=%d\n",i,v);
                    }
            }
        }
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            int fari=find(i);
            if(vis[fari]==0&&wolf[fari]==1)
            {
                ans+=cnt[fari];
 
            }
            vis[fari]=1;
        }
        printf("0 %d\n",ans);
    }
    return 0;
}