模型评估

当我们得到一个机器学习模型，我们需要确定几个指标用来评估模型的预测能力。对于回归分析，主要有mse和R 2 。对于分类算法，评价指标主要有AUC，accuracy，precision等。本文主要介绍相关术语。

回归评价指标

回归是对连续的实数值进行预测，即输出值是连续的实数值，常用判决系数（coefficient of determination ）来评估模型对数据的拟合程度.

对于 m 个样本 (x1,y1),(x2,y2),⋅⋅⋅(xm,ym)
模型估计值为 (x1,y1^),(x2,y2^)⋅⋅⋅(xm,y^m)

样本总平方和 TSS （Total Sum of Squares）:

TSS=∑i=1m(yi−y¯i)2

残差平方和 RSS （Residual Sum of Squares）,又名误差平方和 SSE （Sum of Squares Error）：

TSS=∑i=1m(yi−y^i)2

mse （Mean Square Error）即

mse=TSSm

由公式可知 mse 大于0，越小拟合效果越好，当 mse=0 拟合效果最好。

定义 R2 为

R2=1−RSSTSS

由公式可知， R2 越大表示预测效果越好， R2=1 是其最大值。当预测值为样本期望， R2 为0。 R2 可能为负。sklearn中的线性模型的score返回的是模型的 R2

from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import ElasticNetCV

model = Pipeline([
    ('ss', StandardScaler()),
    ('poly', PolynomialFeatures(degree=3, include_bias=True)),
    ('linear', ElasticNetCV(l1_ratio=[0.1, 0.3, 0.5, 0.7, 0.99, 1], 
        alphas=np.logspace(-3, 2, 5),
        fit_intercept=False, max_iter=1e3, cv=3))
])
model.fit(x_train, y_train.ravel())
linear = model.get_params('linear')['linear']
y_pred = model.predict(x_test)
r2 = model.score(x_test, y_test)
mse = mean_squared_error(y_test, y_pred)
print 'R2:', r2
print u'均方误差：', mse

分类评价指标

  准确率(Accuracy)是指在分类中，测试集中分类正确的样本个数占总个数的比例：

accuracy=ncorrectntotal

  准确率比较简单。但没有对不同类别进行区分，有时候模型是需要比较关注错分类别的，比如在医患诊断中。同时，可能因为数据分布不平衡，即有的类别下的样本过多，有的类别下的样本个数过少，这样会导致样本占大部分的类别主导了准确率的计算。

  为了应对每个类别下样本的个数不一样的情况，对准确率进行优化，计算每个类别下的准确率，然后再计算它们的平均值，当每个类别下的样本个数一样，则平均准确率与准确率相等。 但平均准确率在数据分布不平衡时的准确率可靠性依旧不强。

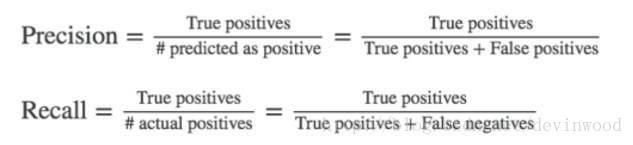
当考虑到数据分布可能不平衡 ① 的情况，其实更多的会使用混淆矩阵（Confusion Matrix）去计算精确率（Precision）&召回率（Recall）,然后在通过Precision&Recall去计算F值(F-score).

混淆矩阵是对分类的结果进行详细描述的一个表，无论是分类正确还是错误，并且对不同的类别进行了区分，如下表：

准确率（P值）是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。

召回率（R值）是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。

公式如下：

综合考虑P值与R值，最常见的方法就是F值，通过计算F值来评价一个指标！

F=2∗P∗RP+R

AUC的全称是Area under the Curve，即曲线下的面积，这条曲线便是ROC曲线，全称为the Receiver Operating Characteristic曲线。

  ROC曲线描述分类器的TPR（True Positive Rate，分类器分类正确的正样本个数占总正样本个数的比例，即R值）与FPR（False Positive Rate，分类器分类错误的负样本个数占总负样本个数的比例）之间的变化关系。

TPR=TPTP+FN  FPR=FPFP+TN

  显而易见，最好的分类器便是FPR＝0%，TPR＝100%，但是一般在实践中一个分类器很难会有这么好的效果，即一般TPR不等于1，FPR不等于0的。当使用ROC曲线对分类器进行评价时，如果对多个分类器进行比较时，如果直接使用ROC曲线很难去比较，只能通过将ROC分别画出来，然后进行肉眼比较，那么这种方法是非常不便的，因此我们需要一种定量的指标去比较，这个指标便是AUC了，即ROC曲线下的面积，面积越大，分类器的效果越好，AUC的值介于0.5到1.0之间。
  
  在二分类中，我们需要设定一个阈值，大于阈值分类正类，否则分为负类。因此，我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中的一些点，连接这些点就形成ROC曲线。当阈值无穷大时，表示点(1,1)，当阈值无穷小，表示点(0,0)，所以ROC曲线必经过(0,0)与(1,1)这两点，实际上这两点的连线形成的ROC代表一个随机分类器，一般情况下分类器的ROC曲线会在这条对角连线上方。
  
  ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中，经常会出现类别不平衡（class imbalance）现象，即负样本比正样本少很多（或者相反），而且测试数据集中的正负样本的分布也可能随时间发生变化。
  

附录

①：改变评判方式是处理不均衡数据时一种办法，当遇到不均衡数据时，还可以尝试以下方法：
1、获取更多数据
2、重组数据，第一种重组方式是复制少数数据里的样本,使其可以达到和多数数据样本差不多的数量，但这种方式增加数据容易改变原有分布，降低模型泛化能力，所以处理时需要考虑数据分布。第二种方式就是对多数样本的数据进行开刀,砍掉一些多数样本的数据,还是使两者的数量差不多。
3、修改算法，调整阈值，或尝试其他机器学习方法，像决策树这样的方法就不会受到不均衡数据的影响。