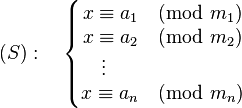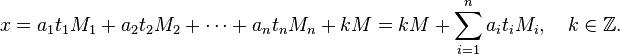中国剩余定理在信息领域的应用
写这边博文是听了台湾张真诚老师的一次讲座，感觉比较有趣。回来后自己查查资料加总结一点就想写下来，坚信好记性不如烂笔头，何况我记性比较差......
中国剩余定理（Chinese Reminder Thereom）
中国剩余定理是数论中的一个关于一元线性同余方程组的定理，说明了一元线性同余方程组有解的准则以及求解方法。也称为孙子定理，古有“韩信点兵”、“孙子定理”、求一术（宋 沈括）“鬼谷算”（宋 周密）、“隔墻算”（宋 周密）、“剪管术”（宋 杨辉）、“秦王暗点兵”、“物不知数”之名。
一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：
有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？
即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。
宋朝数学家秦九韶于1247年《数书九章》卷一、二《大衍类》对“物不知数”问题做出了完整系统的解答。明朝数学家程大位将解法编成易于上口的《孙子歌诀》：
三人同行七十希，五树梅花廿一支，七子团圆正半月，除百零五使得知
这个歌诀给出了模数为3、5、7时候的同余方程的秦九韶解法。意思是：将除以3得到的余数乘以70，将除以5得到的余数乘以21，将除以7得到的余数乘以15，全部加起来后除以105，得到的余数就是答案。比如说在以上的物不知数问题里面，使用以上的方法计算就得到
因此按歌诀求出的结果就是23.
用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：
有解的判定条件，并用构造法给出了在有解情况下解的具体形式。
中国剩余定理说明：假设整数m1, m2, ... , mn两两互质，则对任意的整数：a1, a2, ... , an，方程组
有解，并且通解可以用如下方式构造得到：
- 设
是整数m1, m2, ... , mn的乘积，并设
是除了mi以外的n - 1个整数的乘积。 - 设
为
模
的数论倒数：
- 方程组的通解形式为：
在模
的意义下，方程组只有一个解：
主要应用之一：Ordered Minimal Perfect Hashing Function
Hashtable 是用来存储 key 和 value 对的数据结构 , 根据设定的 hash 函数 H(key) 和处理冲突的方法将一组关键字（ key ）映象到一个有限的连续的地址集（区间）上，并以关键字在地址集中的“象”作为记录在表中存储位置，这种表便成为 hashtable.这种方法有个问题就是有可能会对不同的Key 产生相同的地址映射，就是所谓的冲突。现在有很多解决这个问题的方法，比如开放定址法，再哈希法，链地址法等。这种做法又叫亡羊补牢式做法，还有一种就是在Hash函数上做改进以便找出一个完美的hash函数，对不同的key产生的value映射不会冲突。这种做法又叫未雨绸缪式做法。还有一个问题就是，通过哈希函数散列之后这些数据就是乱序的，即便你能在O（1）时间内读出数据，你也得花至少O（nlogn）的时间来排序。这对于大量的数据来说是非常大的开销。
针对以上问题，张老师他们提出了叫Ordered Minimal Perfect Hashing的hash函数，这个函数理论上可以产生不冲突的有序映射值。
即：one-to-one maping |key space|<=|Address space|（要不然，你只有十个元素，映射到十万个地址空间里，肯定不会冲突了。）
假设有一个key集合{k1，k2，k3,...kn}
则： h（k）=Cmod P(k) .
其中，P(k)为互质数转换函数，即：P(k)能产生一系列互质的数。我查看了ACM上张老师的论文，原文解释对p(x)的解释如下：
We call a function p(x) a prime number function for a<=x<= b, where x, a, and b are all positive integers,There are several such prime number functions. According to Hua [6](Hua, L.G.（这是中国伟大数学家华罗庚的一本书） An Introduction to Number Theory, Sheng-Deng Reading, Taiwan (in Chinese),1975. ), the following are the prime number Functions that have been found.
p(x) =x^2-x+17 for l<=x<= 16 p(x)=x^2-x+ 41 for 1<=x<=40
The book [6], to the best of the author's knowledge, exists only in Chinese. (The author was told that pringer-Verlag will publish an English version of this book.) the following prime number function was reported:
p(x) = x^2 - 81x + 1681 for 41< =x <= 80. 还有一些其他的素数产生函数，可以在很大的范围内产生互质的数。
好了上面hash函数中的P(x)有了数学保证。接下来解释一下公式中的C，这个C就是利用中国剩余定理来产生。
Example：
key set：{20,33,149,238}
利用某个prime 函数可以对上面给出的给进行转换：P(20)=4 P(33)=5 P(149)=7 P(238)=9 。由于这只是原理介绍，没有具体计算到底用的哪个Prime Function。产生了p（k）之后，问题就到了如何产生C了。产生C必然是要用到中国剩余定理：
Cmod4=1，Cmod5=2，Cmod7=3，Cmod9=4 ...这个C就比较好算了。利用公式算得C=157.可以验证，这是一个满足要求的C。这样就可以解决旧hash问题的冲突和无序问题了。
有两个问题是：其一，P（k）函数能否产生足够多的互质数，其二这些质数会不会重复。对于这两个问题，只能是理论上回答，可以。并没有严格的数学证明。
参考资料：
ACM上的张老师论文《The Study of an Ordered Minimal Perfect Hashing Scheme 》
维基百科：http://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86
http://en.wikipedia.org/wiki/Chinese_remainder_theorem