排序算法--冒泡、直接插入,shell
一、排序的概念和基本分类
1、概念
假设含有 n 个记录的序列为{r1,r2,······,rn},其相应的关键字分别为{k1,k2,·····,kn},需确定1,2,······,n的一种排列p1,p2,······,pn,使其相应的关键字满足kp1<=kp2<=·······<=kpn(非递减或非递增关系),即使得序列成为一个按关键字有序的序列{rp1,rp2,······,rpn},这样的操作就称为排序。
2、排序的稳定性
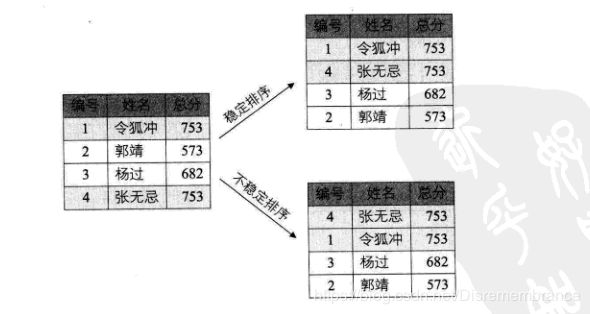
排序的稳定性是指:如果一组数据中两个不同下标的元素相等,它们俩排序之前的序列在排序后仍然保持一致,那就称这个排序方法是稳定的。
如图,令狐冲与张无忌的总分相等,且令狐冲的编号在张无忌之前。那么经过稳定排序方法排序之后,令狐冲仍在张无忌之前。可是经过不稳定排序之后,张无忌超过了令狐冲,本来的次序发生了改变。
3、内排序与外排序
内排序和外排序的区分标准是:根据在排序过程中待排序的记录是否全部被放置在内存中。
- 内排序是在排序整个过程中,待排序的所有记录全部被放置在内存中。
- 外排序是由于排序的记录个数太多,不能同时放置在内存,整个排序过程需要在内外存之间多次交换数据才能进行。
对于内排序来说,排序算法的性能主要受3个方面的影响:
- 时间性能
- 辅助空间
- 算法本身的复杂度
内排序可以分为:
- 插入排序
- 交换排序
- 选择排序
- 归并排序
二、冒泡排序
1、概念和思想
冒泡排序(Bubble Sort)是一种交换排序,它的基本思想是:两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
2、排序过程分析
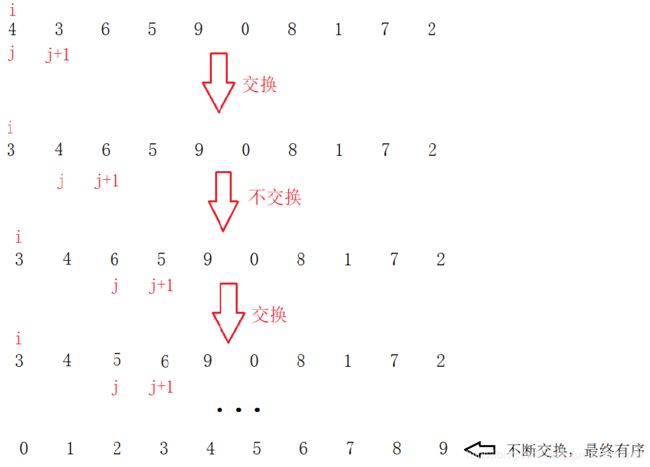
冒泡的排序过程就是不断的与相邻元素进行比较、交换,每一趟冒泡排序都会把最大数交换到最后面。n趟冒泡排序之后,倒数n个元素有序。
3、代码实现
void BubbleSort(int *arr,int len)
{
if (arr == nullptr || len <= 0)
return;
for (int i = 0; i < len - 1; ++i)
{
for (int j = 0; j < len - i - 1; ++j)
{
if (arr[j] > arr[j+1])
{
int tmp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = tmp;
}
}
}
}
这样写的代码,如果它已经有序了,那还得进行内层循环的遍历,时间复杂度会稳定在O(n^2)。
4、冒泡优化
void BubbleSort(int *arr,int len)
{
if (arr == nullptr || len <= 0)
return;
bool flag = false;
for (int i = 0; i < len - 1; ++i)
{
flag = false;
for (int j = 0; j < len - i - 1; ++j)
{
if (arr[j] > arr[j+1])
{
int tmp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = tmp;
flag = true;
}
}
if (!flag)
return;
}
}
优化之后,如果一趟冒泡都没有进行一次数据交换,那就证明该组数据已经有效。有序情况下,时间复杂度是O(n)。冒泡也是一种稳定排序。
三、直接插入排序
1、概念和思想
直接插入排序(Straight Insertion Sort)的基本操作是:将一个元素插入到已经排好序的有序表中,从而得到一个新的、记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
当插入第i(i >= 1)时,前面的V[0],V[1],……,V[i-1]已经排好序。这时,用V[i]的排序码与V[i-1],V[i-2],…的排序码顺序进行比较,找到插入位置即将V[i]插入,原来位置上的元素向后顺移。
2、排序过程分析
插入排序的思想就在于从第i(i>=1)个元素开始,如果arr[i] < arr[j] (0 <= j < i ),那就在0-j位置找一个合适的位置插入进去就OK。

3、代码实现
void InsertSort(int *arr,int len)
{
if (arr == nullptr || len <= 0)
return;
int tmp = 0;
int i = 0;
int j = 0;
for (i = 1; i < len; ++i)
{
tmp = arr[i];
for (j = 0; j < i; ++j)
{
if (tmp < arr[j])
{
break;
}
}
for (int k = i - 1; k >= j; k--)
{
arr[k + 1] = arr[k];
}
arr[j] = tmp;
}
}
这种方式实现的贴合插入排序的思想,但是它是从前往后找合适的位置,最好最坏情况下时间复杂度都为O(n^2)。这样不行,那不妨换一种思路。不能从前往后找,那就从后往前找呗!
4、代码优化
void InsertSort(int *arr,int len)
{
if (arr == nullptr || len <= 0)
return;
int i = 0;
int j = 0;
int tmp = 0;
for (i = 1; i < len; ++i)
{
tmp = arr[i];
for (j = i - 1; j >= 0; --j)
{
if (tmp < arr[j])
{
arr[j + 1] = arr[j];
}
else
break;
}
arr[j + 1] = tmp;
}
}
这样时间复杂度最坏O(n^2),最好O(n),是稳定排序。
四、shell(希尔)排序
1、概念和思想
希尔排序的思想就是:直接插入排序 + 分组
插入排序很好实现,关键就是这个分组,应该怎么分?
假如现在有一组数据,一共15个元素,要分成5组。怎么分?

这样排完一趟之后:

虽然组内有序,但是整体上可以说还是无序。
所以希尔排序的分组要采取跳跃分割的策略,根据要分成的组数来决定跳跃的元素个数。
2、分组和排序过程分析
假设现在有一组数据{20,33,21,54,17,16,30,18,19,22,7,10,46,12,15},要进行shell排序。
首先将它划分成5组,并使得组内有序。

使得组内有序:
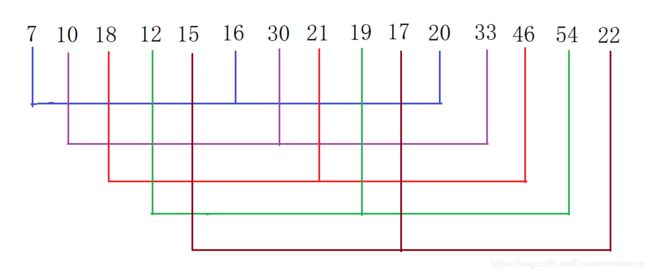
接下来,划分为3组,并使得组内有序。
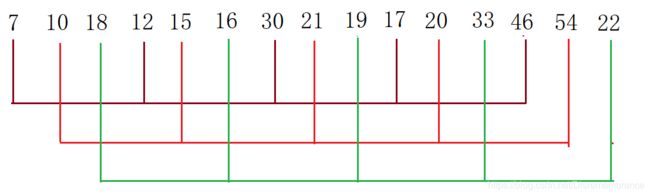
使得组内有序:
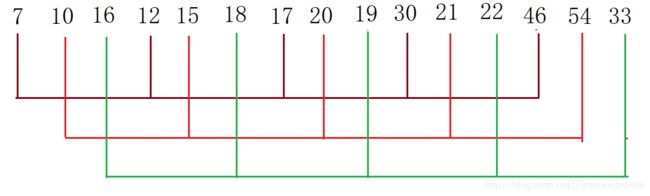
这样得到:7 10 16 12 15 18 17 20 19 30 21 22 46 54 33
这样一组数据已经基本有序了,所以再进行一次整组的插入排序,也可以认为是分为1组,然后在这一组之间进行一次插入排序,那么排完之后,整组数据就全部有序了。
3、代码实现
void Shell(int *arr, int len, int gap)
{
int i = 0;
int j = 0;
int tmp = 0;
for (i = gap; i < len; ++i)
{
tmp = arr[i];
for (j = i - gap; j >= 0;j-=gap)
{
if (arr[j] > tmp)
{
arr[j + gap] = arr[j];
}
else
break;
}
arr[j + gap] = tmp;
}
}
void ShellSort(int *arr, int len)
{
if (arr == nullptr || len < 0)
return;
int gap_arr[] = {5,3,1};
int gap_len = sizeof(gap_arr) / sizeof(gap_arr[0]);
for (int i = 0; i < gap_len; ++i)
{
Shell(arr, len, gap_arr[i]);
}
}
关于组的划分还有一种方式就是,要划分的组数 = len / 3 + 1。这样划分组的方式,也可以使得数据有序。
组数怎么划分,划分为多少组,其实关系不大。重要的是:一定要跳跃式划分,千万不敢连着划分。
shell排序最好的时间复杂度在O(n),最坏在O(n^2)。
平均下来在O(n^1.3-1.5),是不稳定排序。