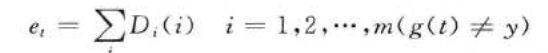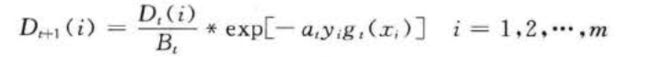一、BP_ Adaboost模型
Adaboost 算法的思想是合并多个“弱”分类器的输出以产生有效分类。其主要步骤为 :
(1)首先给出弱学习算法和样本空间(x, y) ,从样本空间中找出 m 组训练数据,每组训练数据的权重都是 1 /m。
(2)用弱学习算法迭代运算 T 次,每次运算后都按照分类结果更新训练数据权重分布,对于分类失败的训练个体赋予较大权重,下一次迭代运算时更加关注这些训练个体。弱分类器通过反复迭代得到一个分类函数序列 f1, ,f2 , … , fT ,每个分类函数赋予一个权重,分类结果越好的函数,其对应权重越大。
(3)T 次迭代之后,最终强分类函数 F 由弱分类函数加权得 。
BP_Adaboost 模型即把 BP 神经网络作为弱分类器,反复训练 BP 神经网络预测样本输出,通过 Adaboost 算法得到多个 BP 神经网络弱分类器组成的强分类器。
二、BP_ Adaboost模型分类算法流程
基于 BP_Adaboost 模型的 分类算法流程图如下:
算法步骤如下:
step1:数据选择和网络初始化。从样本空间中随机选择 m 组训练数据,初始化测试数据的分布权值 D,(i) = l/m,根据样本输入输出维数确定神经网络结构,初始化 BP 神经网络权值和阈值 。
step2::弱分类器预测。训练第 t 个弱分类器时,用训练数据训练 BP 神经网络并且预测训练数据输出,得到预测序列 g(t)的预测误差和 et,误差和 et的计算公式为
式中, g(t )为预测分类结果,y为期望分类结果 。
step3: 计算预测序列权重 。 根据预测序列 g(t) 的预测误差 et, 计算序列的权重 αt , 权重计算公式为
step4: 测试数据权重调整 。 根据预测序列权重 αt,调整下一轮训练样本的权重,调整公式为
式中, βt是归一化因子,目的是在权重比例不变的情况下使分布权值和为 1 。
step5: :强分类函数 。 训练 T 轮后得到j T 组弱分类函数 f (gt ,at) ,由 T 组弱分类函数 f (gt ,at)组合得到了强分类函数 h(x)
三、BP_ Adaboost模型分类实例
现有某公司财务状况数据共1350组,每组数据共有11维,前10维分别代表公司的分费用利润率、资产营运能力、公司总资产、总资产增长率、流动比亘在、营业现金流量、审计意见类型、每股收益、存货周转率和资产负债率十项指标 ,最后1维代表公司的财务状况,其中1代表该公司财务状况良好,-1则代表该公司财务出现问题。
根据要求,选取其中1000组数据作为训练集,剩余的350组作为测试集,采用的BP神经网络结构为10-6-1,共训练生成10个BP神经网络弱分类器,最后用10个弱分类器组成的强分类器对公司财务进行分类。
利用matlab实现该分类问题,代码如下:
%% 清空环境变量
clc
clear
%% 下载数据
load data input_train output_train input_test output_test
%% 权重初始化
[mm,nn]=size(input_train);
D(1,:)=ones(1,nn)/nn;
%% 弱分类器分类
K=10;
for i=1:K
%训练样本归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
error(i)=0;
%BP神经网络构建
net=newff(inputn,outputn,6);
net.trainParam.epochs=5;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00004;
%BP神经网络训练
net=train(net,inputn,outputn);
%训练数据预测
an1=sim(net,inputn);
test_simu1(i,:)=mapminmax('reverse',an1,outputps);
%测试数据预测
inputn_test =mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
test_simu(i,:)=mapminmax('reverse',an,outputps);
%统计输出效果
kk1=find(test_simu1(i,:)>0);
kk2=find(test_simu1(i,:)<0);
aa(kk1)=1;
aa(kk2)=-1;
%统计错误样本数
for j=1:nn
if aa(j)~=output_train(j);
error(i)=error(i)+D(i,j);
end
end
%弱分类器i权重
at(i)=0.5*log((1-error(i))/error(i));
%更新D值
for j=1:nn
D(i+1,j)=D(i,j)*exp(-at(i)*aa(j)*test_simu1(i,j));
end
%D值归一化
Dsum=sum(D(i+1,:));
D(i+1,:)=D(i+1,:)/Dsum;
end
%% 强分类器分类结果
output=sign(at*test_simu);
%% 分类结果统计
%统计强分类器每类分类错误个数
kkk1=0;
kkk2=0;
for j=1:350
if output(j)==1
if output(j)~=output_test(j)
kkk1=kkk1+1;
end
end
if output(j)==-1
if output(j)~=output_test(j)
kkk2=kkk2+1;
end
end
end
kkk1
kkk2
disp('第一类分类错误 第二类分类错误 总错误');
% 窗口显示
disp([kkk1 kkk2 kkk1+kkk2]);
plot(output)
hold on
plot(output_test,'g')
%统计弱分离器效果
for i=1:K
error1(i)=0;
kk1=find(test_simu(i,:)>0);
kk2=find(test_simu(i,:)<0);
aa(kk1)=1;
aa(kk2)=-1;
for j=1:350
if aa(j)~=output_test(j);
error1(i)=error1(i)+1;
end
end
end
disp('统计弱分类器分类效果');
error1
disp('强分类器分类误差率')
(kkk1+kkk2)/350
disp('弱分类器分类误差率')
(sum(error1)/(K*350))
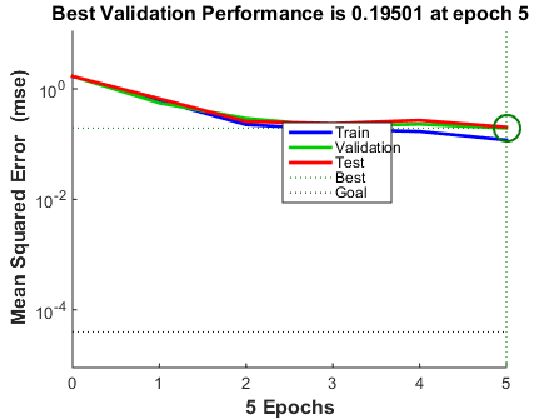
结果如下:
分析结果可以看出,强分类器分类误差率低于弱分类器分类误差率,表明BP_Adaboos分类算法效果还是比较好的。对于案例中的数据,可以再加强训练一下第二类分类的数据,最后使得分类效果更加优良。