obspy中文教程(七)
Visualize Data Availability of Local Waveform Archive(可视化本地波形存档数据的可用性)
通常,您拥有大量数据并希望知道哪个站点在何时是可用的。对于这种假设的情况,obspy提供了obspy-scan脚本(安装后即可用),它能从文件的数据头检测文件格式(MiniSEED, SAC, SACXY, GSE2, SH-ASC, SH-Q, SEISAN, 等),在间隙处绘制为垂直红线,可用数据的在开始时间绘制十字,数据本身绘为水平线。该脚本可以扫描超过1000个文件(已有被用于扫描30000个文件,耗时约45分钟。),自动绘制年/月范围。它会打开一个可放大的交互式绘图窗口。
从命令提示符执行类似下面的语句,使用通配符匹配文件:
$ obspy-scan /bay_mobil/mobil/20090622/1081019/*_1.*Travel Time and Ray Path Plotting(走时和射线路径绘制)
走时绘制
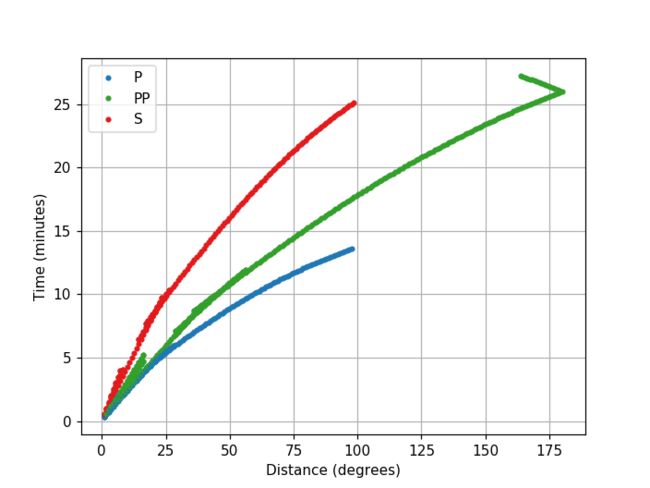
下面的代码展示如何plot_travel_times()函数绘制给定距离和相位的使用iasp91速度模型计算出的走时。
from obspy.taup import plot_travel_times
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax = plot_travel_times(source_depth=10, ax=ax, fig=fig,
phase_list=['P', 'PP', 'S'], npoints=200)
笛卡尔射线路径
下面的几行代码展示了如何绘制给定距离和相位的射线路径。射线路径使用iasp91速度模型计算,并使用obspy.taup.tau.Arrivals类的plot_rays()函数的绘制(在笛卡尔坐标系中)。
from obspy.taup import TauPyModel
model = TauPyModel(model='iasp91')
arrivals = model.get_ray_paths(500, 140, phase_list=['PP', 'SSS'])
arrivals.plot_rays(plot_type='cartesian', phase_list=['PP', 'SSS'],
plot_all=False, legend=True)
球形射线路径
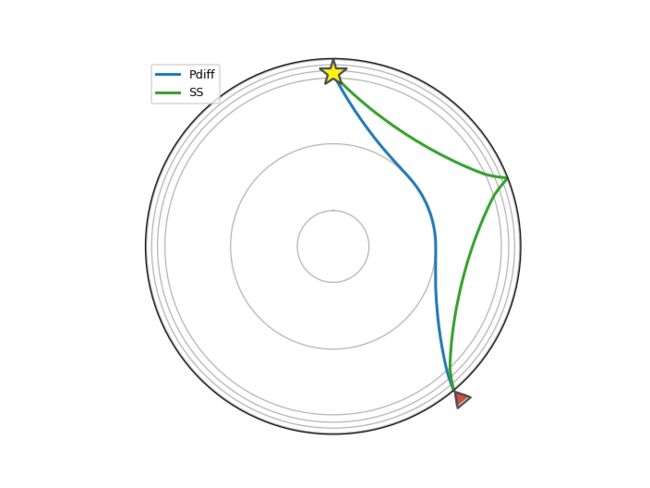
下面的几行代码展示了如何绘制给定距离和相位的射线路径。射线路径使用iasp91速度模型计算,并使用obspy.taup.tau.Arrivals类的plot_rays()函数的绘制(在球形图中)。
多距离射线路径
下面的几行代码展示了如何绘制有多个震中距和相位的射线路径。射线路径使用iasp91速度模型计算,并使用obspy.taup.tau.Arrivals类的plot_ray_paths()函数的绘制(在球形图中)。
from obspy.taup.tau import plot_ray_paths
import matplotlib.pyplot as plt
fig, ax = plt.subplots(subplot_kw=dict(polar=True))
ax = plot_ray_paths(source_depth=100, ax=ax, fig=fig, phase_list=['P', 'PKP'],
npoints=25)对于单个震中距离的射线路径示例,请尝试上一节中的plot_rays()方法。以下是一个更高级的示例,其中包含自定义的相位和距离列表:
import numpy as np
import matplotlib.pyplot as plt
from obspy.taup import TauPyModel
PHASES = [
# Phase, distance
('P', 26),
('PP', 60),
('PPP', 94),
('PPS', 155),
('p', 3),
('pPcP', 100),
('PKIKP', 170),
('PKJKP', 194),
('S', 65),
('SP', 85),
('SS', 134.5),
('SSS', 204),
('p', -10),
('pP', -37.5),
('s', -3),
('sP', -49),
('ScS', -44),
('SKS', -82),
('SKKS', -120),
]
model = TauPyModel(model='iasp91')
fig, ax = plt.subplots(subplot_kw=dict(polar=True))
# Plot all pre-determined phases
for phase, distance in PHASES:
arrivals = model.get_ray_paths(700, distance, phase_list=[phase])
ax = arrivals.plot_rays(plot_type='spherical',
legend=False, label_arrivals=True,
plot_all=True,
show=False, ax=ax)
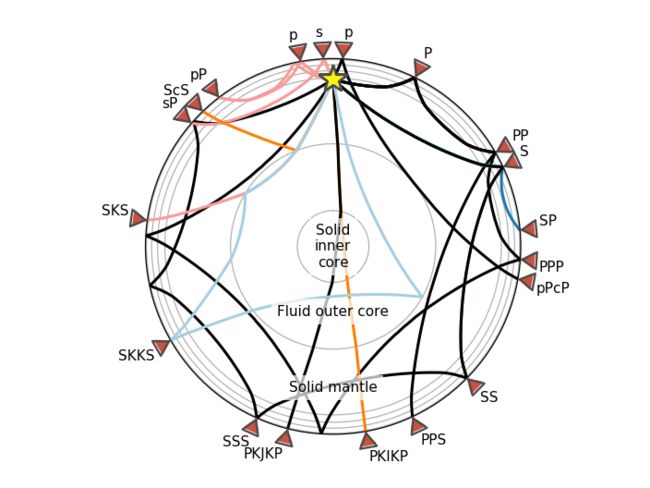
# Annotate regions
ax.text(0, 0, 'Solid\ninner\ncore',
horizontalalignment='center', verticalalignment='center',
bbox=dict(facecolor='white', edgecolor='none', alpha=0.7))
ocr = (model.model.radius_of_planet -
(model.model.s_mod.v_mod.iocb_depth +
model.model.s_mod.v_mod.cmb_depth) / 2)
ax.text(np.deg2rad(180), ocr, 'Fluid outer core',
horizontalalignment='center',
bbox=dict(facecolor='white', edgecolor='none', alpha=0.7))
mr = model.model.radius_of_planet - model.model.s_mod.v_mod.cmb_depth / 2
ax.text(np.deg2rad(180), mr, 'Solid mantle',
horizontalalignment='center',
bbox=dict(facecolor='white', edgecolor='none', alpha=0.7))
plt.show()Cross Correlation Pick Correction(互相关拾取校正)
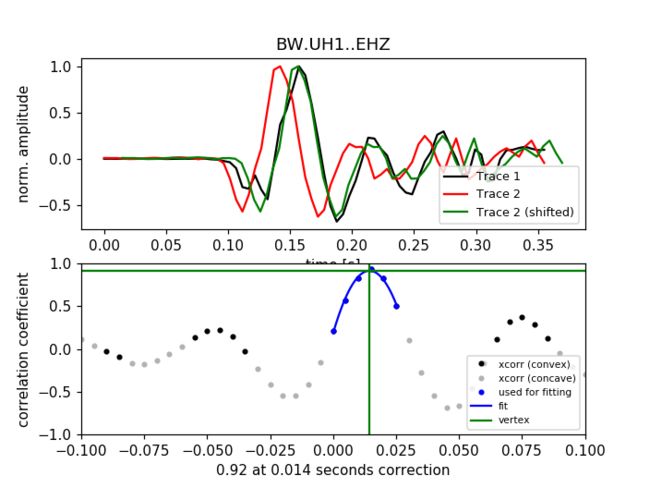
该示例展示如何对齐两个地震的起始波形相位,以便纠正在常规分析中无法完全设置一致的原始拾取时间。按照[Deichmann1992]的方法,互相关函数的凹陷部分最大值附近可用抛物线拟合。
为调整参数并验证检查结果,可以选择展示图形或者将其存为图像文件。参见xcorr_pick_correction()。
该示例将打印拾取序列2的时间校正和相应的相关系数,并打开原始和预处理数据相关性的绘图窗口:
No preprocessing:
Time correction for pick 2: -0.014459
Correlation coefficient: 0.92
Bandpass prefiltering:
Time correction for pick 2: -0.013025
Correlation coefficient: 0.98
from __future__ import print_function
import obspy
from obspy.signal.cross_correlation import xcorr_pick_correction
# read example data of two small earthquakes
path = "https://examples.obspy.org/BW.UH1..EHZ.D.2010.147.%s.slist.gz"
st1 = obspy.read(path % ("a", ))
st2 = obspy.read(path % ("b", ))
# select the single traces to use in correlation.
# to avoid artifacts from preprocessing there should be some data left and
# right of the short time window actually used in the correlation.
tr1 = st1.select(component="Z")[0]
tr2 = st2.select(component="Z")[0]
# these are the original pick times set during routine analysis
t1 = obspy.UTCDateTime("2010-05-27T16:24:33.315000Z")
t2 = obspy.UTCDateTime("2010-05-27T16:27:30.585000Z")
# estimate the time correction for pick 2 without any preprocessing and open
# a plot window to visually validate the results
dt, coeff = xcorr_pick_correction(t1, tr1, t2, tr2, 0.05, 0.2, 0.1, plot=True)
print("No preprocessing:")
print(" Time correction for pick 2: %.6f" % dt)
print(" Correlation coefficient: %.2f" % coeff)
# estimate the time correction with bandpass prefiltering
dt, coeff = xcorr_pick_correction(t1, tr1, t2, tr2, 0.05, 0.2, 0.1, plot=True,
filter="bandpass",
filter_options={'freqmin': 1, 'freqmax': 10})
print("Bandpass prefiltering:")
print(" Time correction for pick 2: %.6f" % dt)
print(" Correlation coefficient: %.2f" % coeff)