图卷积网络

什么是图卷积神经网络？简单的来说就是其研究的对象是图数据（Graph），研究的模型是卷积神经网络。

卷积神经网络

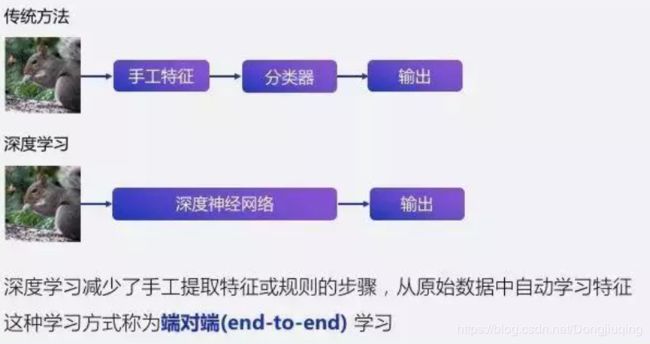
自2012年以来，深度学习在计算机视觉以及自然语言处理两个领域取得了巨大的成功。和传统方法相比，它好在哪里呢？

假设有一张图，要做分类，传统方法需要手动提取一些特征，比如纹理、颜色、或者一些更高级的特征。然后再把这些特征放到像随机森林、SVM等分类器，给到一个输出标签，告诉它是哪个类别。而深度学习是输入一张图，经过神经网络，直接输出一个标签。特征提取和分类一步到位，避免了手工提取特征或者人工规则，从原始数据中自动化地去提取特征，是一种端到端（end-to-end）的学习。相较于传统的方法，深度学习能够学习到更高效的特征与模式。

卷积神经网络很好，但是它研究的对象还是限制在Euclidean domains（欧几里得域）的数据。什么是Euclidean data（欧氏数据）？   Euclidean data最显著的特征就是有规则的空间结构，比如图片是规则的正方形栅格（像素），比如语音是规则的一维序列。而这些数据结构能够用一维、二维的矩阵表示，卷积神经网络处理起来很高效。

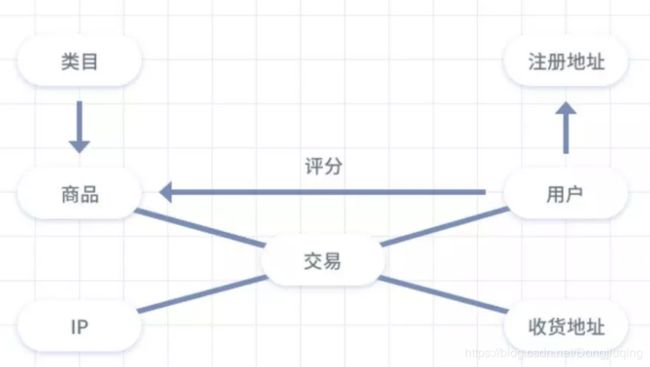
但对于大数据而言，并不时只有图片和文本。比如推荐系统、电子交易、计算几何、脑信号、分子结构等抽象出的图谱。这些图谱结构每个节点连接都不尽相同，有的节点有三个连接，有的节点有两个连接，是不规则的数据结构。图片上每个点都有八个格子相连，而很多其他类型的数据并不是固定连接的。

卷积神经网络的核心过程就是一个加权求和的过程，那么图卷积也相类似。

什么是图卷积网络：

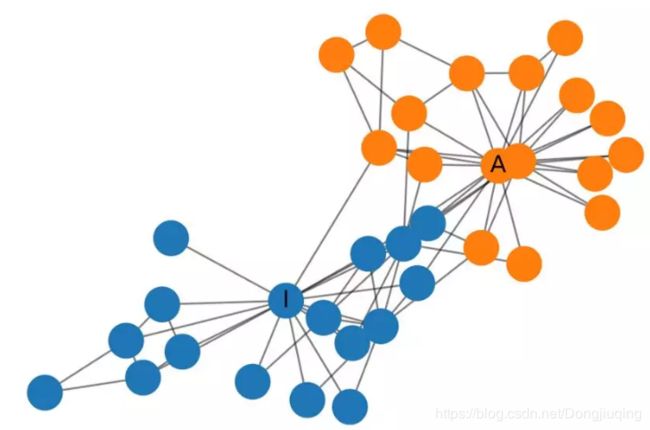
通过上面两个图，可以很明显的感受到，图有两个基本的特性：

一是每个节点都有自己的特征信息。比如人的三维骨架，每个点都有三维坐标数据。

二是图谱中的每个节点还具有结构信息。具体来说就是节点与节点之间相连的信息。

 

 

总的来说，在图数据里面，我们要同时考虑到节点的特征信息以及结构信息，如果靠手工规则来提取，必将失去很多隐蔽和复杂的模式，那么有没有一种方法能自动化地同时学到图的特征信息与结构信息呢？——图卷积神经网络

更形式化地说，图卷积网络（GCN）是一个对图数据进行操作的神经网络。给定图 G = (V, E)，GCN 的输入为：

• 一个输入维度为 N × F⁰ 的特征矩阵 X，其中 N 是图网络中的节点数而 F⁰ 是每个节点的输入特征数。

• 一个图结构的维度为 N × N 的矩阵表征，例如图 G 的邻接矩阵 A。[1]

因此，GCN 中的隐藏层可以写作 Hⁱ = f(Hⁱ⁻¹, A))。其中，H⁰ = X，f 是一种传播规则 [1]。每一个隐藏层 Hⁱ 都对应一个维度为 N × Fⁱ 的特征矩阵，该矩阵中的每一行都是某个节点的特征表征。在每一层中，GCN 会使用传播规则 f 将这些信息聚合起来，从而形成下一层的特征。这样一来，在每个连续的层中特征就会变得越来越抽象。在该框架下，GCN 的各种变体只不过是在传播规则 f 的选择上有所不同 。

 

 

如何理解图卷积算法？

第一步：发射（send）每一个节点将自身的特征信息经过变换后发送给邻居节点。这一步是在对节点的特征信息进行抽取变换。

第二步：接收（receive）每个节点将邻居节点的特征信息聚集起来。这一步是在对节点的局部结构信息进行融合。

第三步：变换（transform）把前面的信息聚集之后做非线性变换，增加模型的表达能力。

 

GCN模型同样具备深度学习的三种性质：

1、层级结构（特征一层一层抽取，一层比一层更抽象，更高级）；

2、非线性变换 （增加模型的表达能力）；

3、端对端训练（不需要再去定义任何规则，只需要给图的节点一个标记，让模型自己学习，融合特征信息和结构信息。）

GCN四个特征：

1、GCN 是对卷积神经网络在 graph domain 上的自然推广。

2、它能同时对节点特征信息与结构信息进行端对端学习，是目前对图数据学习任务的最佳选择。

3、图卷积适用性极广，适用于任意拓扑结构的节点与图。

4、在节点分类与边预测等任务上，在公开数据集上效果要远远优于其他方法。

 

这个链接可以帮助你去理解图卷积网络：https://mp.weixin.qq.com/s/sg9O761F0KHAmCPOfMW_kQ

但是你可能会对其中的数学知识有所疑问，图卷积中用到的一些矩阵的意义，附在这个链接里：

https://blog.csdn.net/lijunweiyhn/article/details/87926425

https://www.cnblogs.com/jzy996492849/p/7250542.html