随机系统(stochastic systems)——以随机游走为例

目录

一杯咖啡是随机的吗？

生活中有许多例子是牛顿力学基本能完全描述的：苹果落地，炮弹轨迹等。这些简单的过程可以由微分方程和初始条件唯一确定。比如知道了炮弹的初始速度和角度，那么后续的轨迹就能用牛顿第二定律唯一解出来。但是生活中还有一些其他的例子，虽然也由牛顿力学控制，但是由于自由度太大，需要描述的参数实在太多，以致理论上的描述和预测根本行不通。自由度很大的系统有哪些？一小勺咖啡里的分子数量就足以说明问题：约有$N=10^{23}$(阿伏伽德罗常数)个分子，每个分子有6个自由度(x,y,z方向的位置和速度)，每个自由度由一个微分方程控制，用目前的计算机解这么多个方程(6N个)组成的微分方程组是不可能完成的任务。

图1. 一杯咖啡里的分子(包括水分子和咖啡分子)个数约为阿伏伽德罗常数。图片摘自http://toddyoungblood.com/。

怎么解决这个问题呢?仔细考察这样的系统会发现，“随机性"承担了很重要的角色。这里的“随机性"可以从不同角度来理解：首先，在这么多粒子的系统中，我们不可能精确知道每个粒子的信息(位置和速度)，这带来了一定的随机性；其次，这个系统可能和外界热源接触或有复杂的相互作用，用统计力学的概率分布和系综平均的方法来描述更合理。因此，即使这一小勺咖啡里的分子都受牛顿力学控制，对于信息的缺失迫使我们不得不使用统计力学描述(“随机性"描述)。实际上，这样的描述是现实世界很好的近似，而且与实验结果能很好符合。

我们就拿咖啡在水中的扩散作为例子。从宏观上看，当我们把咖啡磨成的粉稳稳地倒进一杯热水中时(不人为搅拌)，可以看到咖啡粉不断地向外扩散，直到整杯水都变成褐色。从微观上来看，当我们把一堆咖啡分子(严格来说应该是块状小碎屑，我们不可能把咖啡磨到分子层面，但为了说明方便，暂且用这个叫法)倒进水中后，如果我们能站在其中某个分子上跟着它运动，就会看到如下一幕：这个分子在水中走的轨迹很杂乱，一会儿撞到其他水分子或咖啡分子改变了运动方向和速度，走了一段直线距离(牛顿第一定律)后又撞到另一个分子，又改变了运动方向和速度……前面已经解释过，如果用牛顿运动方程组来求解每个粒子的运动信息，目前的计算能力根本不可能完成；即使能够求解，我们得到的也只是每个粒子的位置和速度随时间的变化而已，对于这个扩散过程本身并不能带来深刻的理解。什么意思呢？举个简单的例子，假设我们求解出了咖啡粉在100ml水中均匀扩散开所需的时间，那么如果想知道在200ml的水中完全扩散的时间，是不是还得重新计算一遍？多麻烦呀！没关系，这个咖啡杯问题我们马上就能解答。

图2. 一团咖啡分子（红色）在水中的溶解，注意到红色粒子之间会相互碰撞改变速度方向和大小。不过这个动画描述的过于简单，没有画出水分子，也没有展现水分子和咖啡分子碰撞的效应。图片摘自http://cronodon.com/BioTech/Diffusion.html。

换个角度看待上述不可能求解的方程：受牛顿力学控制的方程组自由度那么大，其实里面包含的信息是冗余的；我们没必要知道那么多信息，只要用一种统计的描述就够了，也就是对所有分子轨迹的平均行为进行描述即可。因为粒子数足够多，这个求平均的操作也就能很好定义。

现在我们到了最关键的一步：既然我们只想知道平均意义下的系统的行为，我们就可以对真实系统建模，用一个随机过程来近似一个(受牛顿力学控制的)确定的过程，建模的要求是这两个过程具有相同的平均行为。这里的“确定的过程"指的是上述庞大的牛顿方程组的确定解。具体来说，我们把每个粒子不断受撞击而产生的复杂轨迹建模成一个“随机游走"过程，就像深夜一个醉汉在马路上晃悠一样，没有别人推搡，自己在那乱走；而且我们假设这种粒子的随机“乱走"在行为表现上等效于真实的不断受到撞击的走法。这种近似在多大程度上是合理的，我们在后面会提到。

图3. 随机行走(random walk)，或醉汉行走。图片摘自George Gamov, 1961。 图4. 800个粒子构成的热力学系统的模拟，蓝线为其中5个粒子的轨迹，红色为其中一个粒子的速度向量。当系统里的粒子数足够大时，单个粒子的行为可以用随机游走模型来近似。图片摘自Wikipedia：Brownian motion。

从上面的讨论中，我们已经差不多达成了一致：可以用随机游走模型来等效描述咖啡在水中的扩散行为。**一杯咖啡是确定的，但是为了理解它的行为，我们通过建立模型引入了随机性。**现在我们需要讲一点硬核的物理了。

随机游走与扩散

限于篇幅，我们在这里只讨论简单的情况：一维固定步长的无漂移随机游走（取那么长的名字是为了更严谨）。假设每个粒子只能沿着一条直线运动，每次只能向左或向右随机走一步，那么在走了第N步后，我们可以对这些粒子的位置$x_N={\sum }_{n=1}^N{s}_n$有哪些认知呢？上式中$s_n=k_{n}L$，$L$表示每一步的固定步长，$k_N$以相同的可能性取$\pm 1$。

首先，从对称性的角度来讲，每一步位移向左或向右是等概率的，均值为零（$<s_n>=0$），因此对所有粒子随机游走的轨迹求平均不会在任何方向上有系统性的偏移（你会看到一杯咖啡自己沿着桌子跑吗？）。于是，$$<x_N>=\sum _{n=1}^N<s_n>=0$$这里的平均严格来说指的是统计力学中的系综平均。

其次，我们来看位移的方均值（在平均值附近的涨落；或二阶矩，因为均值为零）。$$<x_N^2>=<(x_{N-1}+k_{N}L{)}^2>=<x_{N-1}^2>+2L<x_{N-1}{k}_N>+L^2<k_N^2>$$
因为每一步的$k_N$与前一步的位置$x_{N-1}$相互独立，而$<k_N>=0$，所以最右边中间一项的贡献为零($<x_{N-1}{k}_N>=<x_{N-1}><k_N>=0$)。最后一项正好等于$L^2$，因为$(\pm 1{)}^2=1$。

上式表明第N步的$<x_N^2>$比上一步的$<x_{N-1}^2>$大$L^2$，以此类推，得到$$<x_N^2>=N{L}^2$$
把上式改写一下，如果我们等待的时间为$t$，那么粒子走了$N=t/\Delta t$步，其中$\Delta t=1s$。于是，一维固定步长的无漂移随机游走的方均位移随着时间线性增加：$$<x_N^2>=2Dt$$ 其中扩散常数$D=L^2/(2\Delta t)$，这个常数也可通过实验来追踪大量咖啡颗粒，对他们的位移方均值随时间的变化曲线取平均得到（基本上是一条过原点的直线）。

图5. 一维固定步长随机游走的方均位移随步数（等效于时间）变化关系，左边是两个独立的粒子位移随时间变化关系，右边是对500个这样的粒子位移的方均值随时间的变化曲线求平均，基本上可以用一条过原点的直线拟合。图片摘自Nicholas J. Giordano & Hisao Nakanishi[^Nicholas]。 [^Nicholas]: Giordano, Nicholas J. Computational physics. Pearson Education India, 2006.

这里的求平均符号需要仔细对待——任意某一个粒子的随机游走并不满足上式的扩散定律，我们在讨论的是足够多个粒子的平均行为。此外要说明的是，一个匀速直线运动的物体位移随时间的变化是线性的$x=vt$，而一个随机游走的粒子不一样，位移的方均根随时间变化关系在平均行为上表现为$\sqrt{<x^2>}\sim t^{1/2}$，也就是随时间的增长率要慢一些（指数比1小）。现在我们可以回答前面的咖啡杯问题了，我们假设当$\sqrt{<x^2>}$增长到与杯子尺寸相当时，咖啡粉在水中完全扩散开，那么当杯子尺寸加倍时，$t$要变为$4t$，即需要等待原来四倍的时间他们才能充分混合。

从更深层的视角来看，上述扩散定律连接了宏观和微观世界。我们将咖啡粉的布朗运动作为微观世界（主要是水分子热运动造成的效应）和宏观世界（可用肉眼测量的量）之间联系的桥梁。具体来说，我们已经得到了咖啡粉布朗运动的微观参数（步长$L$和间隔时间$\Delta t$）和宏观可测量量（扩散常数D）之间的关系。

这个扩散定律还可推广到更高维的情形。在二维棋盘上，每步的位移$r$有$x$, $y$两个独立方向，因此有$$<r_N^2>=<x_N^2>+<y_N^2>=4Dt$$ 类似的，三维情形得到$<r_N^2>=6Dt$。

注：维度越高，时间t前面的系数越大，意味着越容易扩散。这是合理的：更高的维度意味着粒子可以从其他维度的路径走到目的地。

最后，我们来看一下$x_N^2$的涨落。这个量说的是粒子个体之间的涨落差异大小。这么说有点不好理解，具体一点，这个量可以理解为两个从同一地点出发，独立做随机游走的粒子的位移方均值的差异。我们想要知道的是，这个差异随着步数（或时间）是越来越大（发散）还是越来越小（收敛）?在继续阅读前，我建议大家花几秒时间思考一下这个问题。
……1s
……2s
……3s
好了，我们直接上公式：
$$\sqrt{<(x_N^2-<x_N^2>{)}^2>}=\sqrt{<x_N^4>-<x_N^2{>}^2}$$
上式中$<x_N^2>$是前面已经算过的，只需要计算四阶矩$<x_N^4>$。
$$<x_N^4>=\sum _{i,j,k,l=1}^N<s_i{s}_j{s}_k{s}_l>$$
这个求和号一共包含$N^4$项，但是由于每一步移动相互独立，导致了不同下标$i$的$s_i$相互独立。因此只要有至少一个下标“落单"，这一项就为零。非零项只有四个下指标均相同，或下指标能两两配对（但不相同，与前一种情况区别开）这两种情况。所以只剩下
$$<x_N^4>=\sum _{i=1}^N<s_i^4>+3\sum _{p=1}^N\left[s_p^2\sum _{q̸=p}{s}_q^2\right]=3N^2{L}^4-2N{L}^4$$
代入前面$x_N^2$的涨落公式，得
$$\sqrt{<(x_N^2{)}^2-<x_N^2{>}^2}=\sqrt{2N^2{L}^4-2N{L}^4}\sim \sqrt{2}N{L}^2$$
最后一个近似当$N$足够大时成立。
这个结果有没有出乎你的意料？它说明$x_N^2$的涨落竟然也随着$N$的增大而变大！也就是两个从同一地点出发独立地做随机游走的粒子越往下走就会离的越远！这和我们之前的对于位置的方均值的讨论是类似的：单个粒子的随机游走，与多个粒子随机游走的平均行为，并不相同。

扩散定律是普适的

至此我们都在讨论最简单的模型：一维固定步长的无漂移随机游走。当然还有其他更接近真实情况也更复杂的模型，比如每一步的步长在某个连续或离散区间里取值，或者每一步的步长可以无限制地取任意长度($Levyflight$)。但是不管模型如何建立，只要给定独立随机移动的步长分布，扩散定律依旧成立，只是系数会有所不同。

我们举步长取某个离散分布的情况作简要说明，假设$P_k$定义为步长为$kL$的概率，其中$k$是一个整数，可正可负，分别代表前进后退。这个模型中，位移的方均值为
$$variance(x_N)=2Dt,其中D=\frac{L^2}{2\Delta t}\times variance(k)$$
依旧满足扩散定律。其中$varience$表示方差。具体推导可以参考Philip Nelson书¹的第四章。

这个结论说明，扩散定律是普适的，定律本身并不依赖于模型，只有系数才依赖于具体的细节。换句话说，对模型的假设做修正只是改变数学的复杂程度，并不改变其物理实质。

##由扩散支配的亚细胞世界
前面说了这么多枯燥的数学，这些结论有什么用？其实，在远比我们小的尺度上，扩散是非常重要的一个过程。没有它，生命可能无法存活。

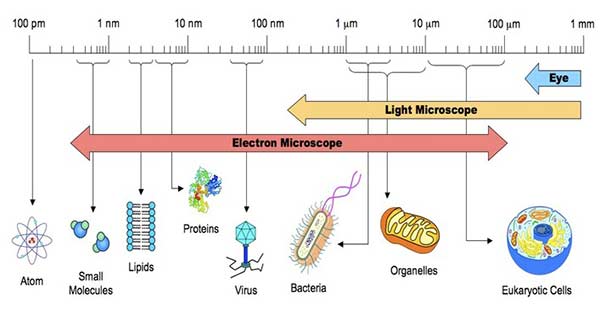图6. 不同尺度下的世界。 图片摘自https://microbiologyinfo.com/different-size-shape-and-arrangement-of-bacterial-cells/。 我们从上图的中间可以看到，细菌的尺寸在$1\mu m$左右(约头发丝的1/50倍)。假设一个细菌可以看成半径为$1\mu m$的小水球，并假设在水球中心放入一些糖分子，大概需要多长时间，这些糖分子才能均匀扩散到整个细菌？换做是细胞大小的水球（$半径10\mu m$）呢？

对于室温下水中的小分子，扩散系数的大小为$D\approx 10^{-9}{m}^2/s^{-1}$，或者写为$D\approx 1\mu m^{2}m{s}^{-1}$。于是，在细菌中的糖分子需要时间$(1\mu m{)}^2/(6D)\approx 0.2ms$就能扩散开来。而在比它尺寸大一个数量级的细胞中，要花100倍于此的时间。这说明，如果想要在微米级别传递物质或信息，仅仅扩散就够了，不需要花力气设计复杂的结构，这或许也是细菌结构下相对简单的原因之一吧。

另一方面，如果想要在长距离传输物质，比如从你看到远处的狮子后大脑发出信号，再通过脊髓传递到腿部的肌肉神经（约1m长的距离）撒腿逃跑，这个信号传递过程如果仅凭扩散来完成的话你早就被吃掉了，于是神经元细胞自己发展出了一套高速传递信息的方式：电信号。当然，在不同神经元之间的突触间隙（约20-30nm）中，神经递质也是通过扩散来传递的。

多说一句，这个扩散的粒子流（前一个神经元流到后一个神经元）并不是由于浓度大的地方粒子之间相互推挤而向把他们浓度低的地方驱赶，因为我们假设所有递质粒子相互独立，也就是没有任何相互作用（我们认为神经递质的数量远小于周围水分子的数量）。导致这个粒子流的合理解释是：由于每个粒子向各个方向运动的概率是均等的，那么粒子多的地方会有更多粒子跑到粒子少的地方。**这是一个由“概率"驱动的流动。**这个概念与“熵"以及“熵力"紧密相连，有机会再细说。

图7. 神经突触示意图。（右下角）神经递质被释放后，向另一边扩散。 图片摘自https://upload.wikimedia.org/wikipedia/commons/3/30/Chemical_synapse_schema_cropped.jpg。

摩擦与扩散是一对双胞胎——爱因斯坦关系

最开始我们对咖啡分子在水中溶解的过程有过唯象的描述，现在我们再来审视一下这个过程。依旧做一些比较强的假设来简化计算。考察一维运动，假设每次碰撞间隔都是$\Delta t$，在两次碰撞之间颗粒的运动遵循牛顿定律$$\Delta x=v_0\Delta t+\frac{1}{2}\frac{f}{m}(\Delta t{)}^2$$其中施加在粒子上的外力$f$可以是电场对该带电粒子的力，也可以是重力等。

另假设每次碰撞消去了碰撞之前的所有记忆，因此$v_0$随机地指向左边或右边，均值为零。对上式求平均得到$$<\Delta x>=\frac{f}{2m}(\Delta t{)}^2$$这个式子表明，在施加了力场后，粒子沿着力的方向有个恒定速度的漂移，平均漂移速度为$$v_{drift}=\frac{<\Delta x>}{\Delta t}=f/\zeta$$上式中粘性摩擦系数$$\zeta =2m/\Delta t$$可以看到这个漂移速度正比于外力的大小。

$\zeta$可以通过实验测量。球体的粘性摩擦系数和半径服从简单的关系，即斯托克斯公式$\zeta =6\pi \eta R$。室温下水的粘度约为$\eta =10^{-3}kg{m}^{-1}{s}^{-1}$。因此只要测得了颗粒的尺寸，就能得到$\zeta$，进一步测量密度可以间接测量颗粒的质量$m$。有了实验能够测量的$\zeta$和$m$，那么碰撞的时间间隔$\Delta t$就可以由$\zeta =2m/\Delta t$计算出来。进一步，从扩散定律$D=L^2/(2\Delta t)$就可以得到分子尺度的特征步长$L$。

目前为止，上述理论有一个致命的缺陷：我们不可能在实验中观测到$\Delta t$和$L$，因此这个理论无法证伪。

所幸的是，爱因斯坦注意到在$\Delta t$和$L$之间还有另一个关系。记特征速度为$v=L/\Delta t$，统计力学告诉我们，（一维）理想气体分子热运动满足$$m<v^2>=k_{B}T$$

现在我们未知的只是$\Delta t$和$L$两个变量，但是有粘性摩擦定律，扩散定律，还有热运动速度的关系式三个方程构成了超定方程，唯一的可能是参数$\zeta$和$D$并非独立，而是有个特定关系，这个关系就是爱因斯坦关系。$$\zeta D=k_{B}T（爱因斯坦关系）$$

这个关系由爱因斯坦在1905年得到，它表明颗粒扩散系数（描述位置的涨落）和粘性摩擦系数（描述颗粒受到的耗散）相互联系。

爱因斯坦关系具有深刻的含义。通过它我们可以从宏观测量推测出分子的大小，而不需要用高端的显微镜来完成。我们知道1mol理想气体的体积为22.4L（0℃，1标准大气压），通过理想气体状态方程$PV=nRT$可以算出气体常数$R=k_B{N}_a$。而实验参数能够给出$k_B$，于是我们知道了阿伏伽德罗常数$N_a$，从而可以估算分子的尺寸。

此外，爱因斯坦关系等号右边没有质量$m$，这说明该关系不依赖于颗粒的质量。颗粒质量越大，扩散起来越难（D越小），且摩擦阻力越大（$\zeta$越大）。这种普适性也提供了可证伪的预言：我们可以检查不同颗粒质量、温度、尺寸条件下，是否都能给出相同的$k_B$值。另外，尽管$\zeta$和$D$与温度的关系很复杂，但他们的乘积与温度的关系却非常简单。值得称道的是，这个关系已经被实验完美证实。

爱因斯坦关系溯源——涨落耗散定理

一个优美的物理关系背后一定有客观存在的真理。爱因斯坦关系其实是一个更普适的定理在随机游走问题中的体现——涨落耗散定理(Fluctuation-dissipation theorem)。涨落耗散定理是统计物理中非常重要而且有意思的话题，一方面在于深入地理解近平衡体系中响应与关联的关系；另一方面在于非平衡态体系中的涨落耗散关系。关于这些内容在其他地方讨论。

---

1. Nelson, Philip. Biological physics. New York: WH Freeman, 2004. ↩︎