数据结构之无向图的连通分量和生成树
上一篇博客介绍了图的遍历,那么这篇博客就介绍利用图的遍历算求解无向图的连通性问题,正如题目所说介绍无向图的连通分量和生成树问题。那么有人会问什么是连通分量,如果不想再去找离散数学来看,请看这里维基百科和百度百科。
1.无向图的连通分量:
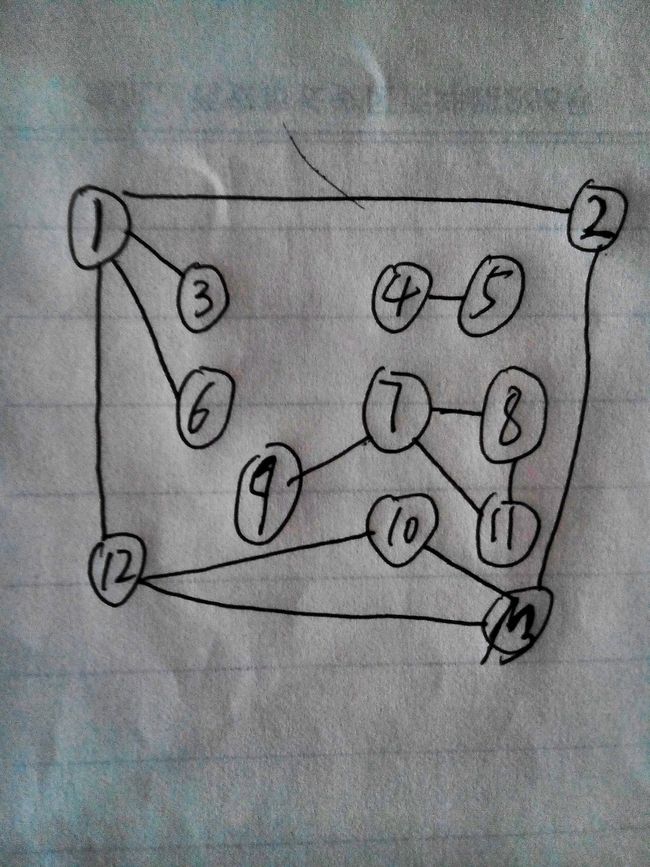
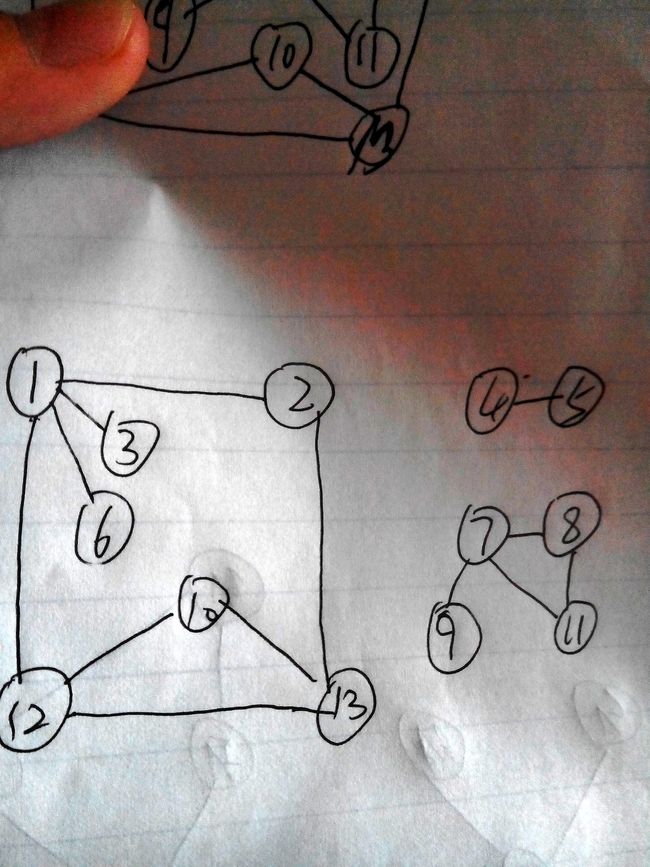
在对无向图进行遍历时,对于连通图,仅需从图中任一顶点出发,进行深度优先搜索或广度优先搜索,便可访问到图中所有顶点。对非连通图,则需从多个顶点出发进行搜索,而每一次从一个新的起始点出发进行搜索过程中得到的顶点访问序列恰为其各个连通分量中的顶点集。例如,上图是一个非连通图,按照图进行深度优先搜索遍历,需调用三次DFS(即分别从顶点1,4和7点出发),得到的顶点访问序列分别为:
看完上面的定义,想必你已经想到判断一个图是否有连通分量/有几个连通分量的办法了.其实要想判定一个无向图是否为连通图,或有几个连通分量,就可设一个计数变量count,初始时取值为0,在深度优先搜索遍历的第二个for 循环中,每调用一次DFS,就给count 增1。这样,当整个算法结束时,依据count 的值,就可确定图的连通性和个数了。
2.生成树
设E(G)为连通图G 中所有边的集合,则从图中任一顶点出发遍历图时,必定将E(G)分成两个集合T(G)和B(G),其中T(G)是遍历图过程中历经的边的集合;B(G)是剩余的边的集合。显然,T(G)和图G 中所有顶点一起构成连通图G 的极小连通子图。并且由深度优先搜索得到的为深度优先生成树;由广度优先搜索得到的为广度优先生成树。那么如果是非连通图怎么办呢?就把非连通图中的连通分量理解为连通图,这样经过深度优先搜索遍历和广度优先搜索遍历就得到了森林,有几个连通分量就有几颗生成树。
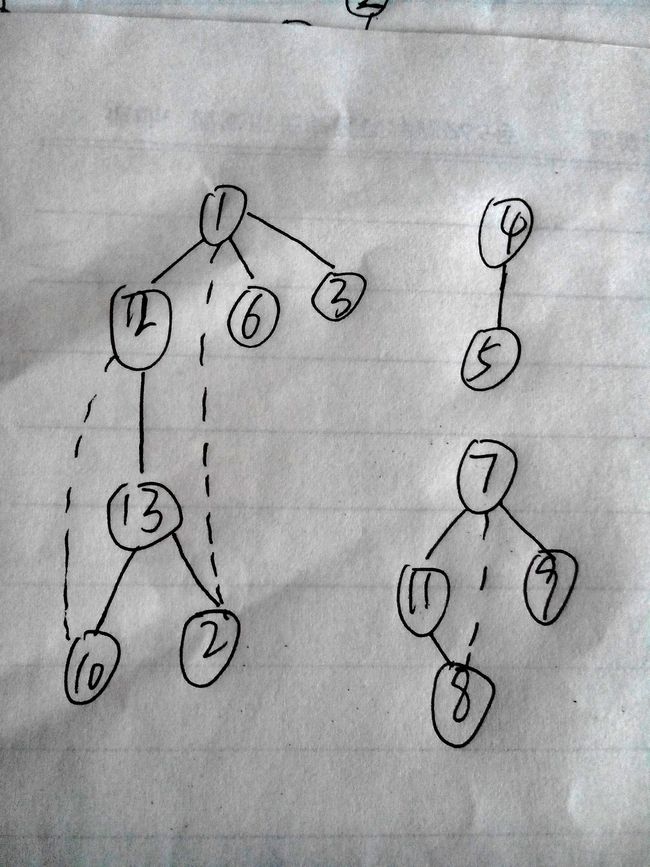
这里我个人感觉存在一种思想,图非常的复杂于是就尽可能的把复杂的问题转换为“简单”的问题---》树,而树又可以转化为链表(当然这里的转换并不“真的”转换为之,而是用相关的思想来理解。这是我的胡思乱想,呵呵)。这里的无向图的三个连通分量即三颗生成树,那么我们假设以孩子兄弟链表作生成森林的存储结构.
这是树中节点的数据结构:
//树的数据类型
typedef int TElemType;
//树的节点数据结构
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild;
struct BiTNode *rchild;
}*BiTree,*Position;
我这里使用数组表示法来表示图,当然也可以用其他的表示。具体的代码这里就不上了,可以看我之前的博客图的数组表示法 也可以看我放在GitHub上的代码
建立生成森林的代码如下:
/*
* @description:建立无向图的深度优先生成森林的孩子兄弟链表T
*/
void DFSForest(MGraph G,BiTree *T) {
int i;
BiTree p,q;
*T = p = q = NULL;
for(i = 0; i < G.vexnum; i++)
visited[i] = FALSE;
for(i = 0; i < G.vexnum; i++) {
if(!visited[i]) {
p = (BiTree) malloc(sizeof(struct BiTNode));
if(!p)
exit(OVERFLOW);
p->data = GetVex(G,i);
p->rchild = NULL;
p->lchild = NULL;
//第一颗生成树的根
if(!(*T))
*T = p;
//其他生成树的根,第一颗树的兄弟
else
q->rchild = p;
q = p; //q指示当前生成树的根
DFSTree(G,i,&p);
}
}
}
/*
* @description:从v出发进行深度优先遍历,生成以T为根节点的生成树
*/
void DFSTree(MGraph G,int v,BiTree *T) {
BiTree p,q;
int first,w;
p = q = NULL;
visited[v] = TRUE;
first = TRUE;
for(w = FirstAdjVex(G,GetVex(G,v)); w >= 0 ; w = NextAdjVex(G,GetVex(G,v),GetVex(G,w))) {
if(!visited[w]) {
p = (BiTree) malloc(sizeof(struct BiTNode));
if(!p)
exit(OVERFLOW);
p->data = GetVex(G,w);
p->rchild = NULL;
p->lchild = NULL;
if(first) {
(*T)->lchild = p;
first = FALSE;
}
else
q->rchild = p;
q = p;
DFSTree(G,w,&q);
}
}
}
简单分析 :结合所给的非连通图可以看出,DFSForest中的第二个循环的作用是生成三颗分别以1,4,7为根节点的生成树(请注意这里的生成树非彼树,请看图),而DFSTree则负责以上面的三个根节点使用递归的思想来生成子树。生成树的过程是对一个连通分量的深度优先搜索遍历过程,则生成森林的过程就是对整个图深度优先搜索遍历的过程。还有就是这里其实只生成了一棵树,即1,4,7其实是兄弟节点的概念,则我们可以用树中的遍历方法来遍历这颗“大树”。
/*
* @description:前序遍历二叉树
*/
Status PreOrderTraverse(BiTree T,Status (*visit) (TElemType elem)) {
if(T) {
if(visit(T->data))
if(PreOrderTraverse(T->lchild,visit))
if(PreOrderTraverse(T->rchild,visit))
return OK;
return ERROR;
}
return OK;
}
测试:
/*---------------------------------------------------------------------------------
* file:MGraph.c
* date:10-9-2014
* author:[email protected]
* version:1.0
* description:图的数组表示及基本操作
------------------------------------------------------------------------------------*/
#include
#include "mgraph.h"
int main(int argc,char *argv[]) {
MGraph G;
BiTree T;
//建图
CreateGraph(&G);
//深度优先遍历图
DFSTraverse(G,PrintElem);
printf("\n");
DFSForest(G,&T);
PreOrderTraverse(T,PrintElem);
printf("\n");
/*
测试用例:
please enter the kind of the graph:2
please enter vexnum, arcnum is info(1 or 0):13,13,0
the value of each vertex:0,1,2,3,4,5,6,7,8,9,10,11,12
please 13 heads and 13 tails:
0,1
0,2
0,5
0,11
1,12
3,4
6,7
6,8
6,10
7,10
9,11
9,12
11,12
0 1 12 9 11 2 5 3 4 6 7 10 8
0 1 12 9 11 2 5 3 4 6 7 10 8
*/
} 完整源码请看:GitHub