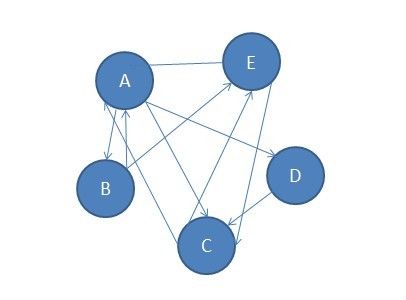
java 实现pagerank
1)A网页有链接指向B,C,D
2)B网页有链接指向A,E
3)C网页有链接指向A,E
4)D网页有链接指向C
5)E网页有链接指向A,C
其关系如下:
根据此图可得出
这里假设每个网页的权重相等,都为1,这个S矩阵是这样得出来的,第1列是A号网页,它指向了B,C,D号网页,它的权重为1,所以B,C,D每个获得的为1/3,这样依次类推。
求解G的特征向量可以通过q(next)=G*q(cur)这样不断迭代获得,已经证明,q(next)与q(cur)最终会收敛。刚开始q可以去一个随机的向量
这里,通过编程求解pagerank,取alpha=0.85,通过不断的迭代,当q(next)和q(cur)之间的距离小于0.0000001时,认为已经收敛。pagerank就是特征值为1的特征向量,A,B,C,D,E号网页的价值分别为特征向量中对应维的值。
为了便于观察结果,这里q取值为
2.14335103032906, 0.4690253246490811, 0.152093449701467, 2.751926907462932 ,2.354654214646654
用List泛型作为向量和矩阵的容器,顺便熟悉一下容器类的使用。java代码如下:
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class PageRank {
private static final double ALPHA = 0.85;
private static final double DISTANCE = 0.0000001;
public static void main(String[] args) {
// List q1=getInitQ(4);
System.out.println("alpha的值为: " + ALPHA);
List q1 = new ArrayList();
q1.add(new Double(2.14335103032906));
q1.add(new Double(0.4690253246490811));
q1.add(new Double(0.152093449701467));
q1.add(new Double(2.751926907462932));
q1.add(new Double(2.354654214646654));
System.out.println("初始的向量q为:");
printVec(q1);
System.out.println("初始的矩阵G为:");
printMatrix(getG(ALPHA));
List pageRank = calPageRank(q1, ALPHA);
System.out.println("PageRank为:");
printVec(pageRank);
System.out.println();
}
/**
* 打印输出一个矩阵
*
* @param m
*/
public static void printMatrix(List> m) {
for (int i = 0; i < m.size(); i++) {
for (int j = 0; j < m.get(i).size(); j++) {
System.out.print(m.get(i).get(j) + ", ");
}
System.out.println();
}
}
/**
* 打印输出一个向量
*
* @param v
*/
public static void printVec(List v) {
for (int i = 0; i < v.size(); i++) {
System.out.print(v.get(i) + ", ");
}
System.out.println();
}
/**
* 获得一个初始的随机向量q
*
* @param n
* 向量q的维数
* @return 一个随机的向量q,每一维是0-5之间的随机数
*/
public static List getInitQ(int n) {
Random random = new Random();
List q = new ArrayList();
for (int i = 0; i < n; i++) {
q.add(new Double(5 * random.nextDouble()));
}
return q;
}
/**
* 计算两个向量的距离
*
* @param q1
* 第一个向量
* @param q2
* 第二个向量
* @return 它们的距离
*/
public static double calDistance(List q1, List q2) {
double sum = 0;
if (q1.size() != q2.size()) {
return -1;
}
for (int i = 0; i < q1.size(); i++) {
sum += Math.pow(q1.get(i).doubleValue() - q2.get(i).doubleValue(),
2);
}
return Math.sqrt(sum);
}
/**
* 计算pagerank
*
* @param q1
* 初始向量
* @param a
* alpha的值
* @return pagerank的结果
*/
public static List calPageRank(List q1, double a) {
List> g = getG(a);
List q = null;
while (true) {
q = vectorMulMatrix(g, q1);
double dis = calDistance(q, q1);
System.out.println(dis);
if (dis <= DISTANCE) {
System.out.println("q1:");
printVec(q1);
System.out.println("q:");
printVec(q);
break;
}
q1 = q;
}
return q;
}
/**
* 计算获得初始的G矩阵
*
* @param a
* 为alpha的值,0.85
* @return 初始矩阵G
*/
public static List> getG(double a) {
int n = getS().size();
List> aS = numberMulMatrix(getS(), a);
List> nU = numberMulMatrix(getU(), (1 - a) / n);
List> g = addMatrix(aS, nU);
return g;
}
/**
* 计算一个矩阵乘以一个向量
*
* @param m
* 一个矩阵
* @param v
* 一个向量
* @return 返回一个新的向量
*/
public static List vectorMulMatrix(List> m,
List v) {
if (m == null || v == null || m.size() <= 0
|| m.get(0).size() != v.size()) {
return null;
}
List list = new ArrayList();
for (int i = 0; i < m.size(); i++) {
double sum = 0;
for (int j = 0; j < m.get(i).size(); j++) {
double temp = m.get(i).get(j).doubleValue()
* v.get(j).doubleValue();
sum += temp;
}
list.add(sum);
}
return list;
}
/**
* 计算两个矩阵的和
*
* @param list1
* 第一个矩阵
* @param list2
* 第二个矩阵
* @return 两个矩阵的和
*/
public static List> addMatrix(List> list1,
List> list2) {
List> list = new ArrayList>();
if (list1.size() != list2.size() || list1.size() <= 0
|| list2.size() <= 0) {
return null;
}
for (int i = 0; i < list1.size(); i++) {
list.add(new ArrayList());
for (int j = 0; j < list1.get(i).size(); j++) {
double temp = list1.get(i).get(j).doubleValue()
+ list2.get(i).get(j).doubleValue();
list.get(i).add(new Double(temp));
}
}
return list;
}
/**
* 计算一个数乘以矩阵
*
* @param s
* 矩阵s
* @param a
* double类型的数
* @return 一个新的矩阵
*/
public static List> numberMulMatrix(List> s,
double a) {
List> list = new ArrayList>();
for (int i = 0; i < s.size(); i++) {
list.add(new ArrayList());
for (int j = 0; j < s.get(i).size(); j++) {
double temp = a * s.get(i).get(j).doubleValue();
list.get(i).add(new Double(temp));
}
}
return list;
}
/**
* 初始化S矩阵
*
* @return S
*/
public static List> getS() {
List row1 = new ArrayList();
row1.add(new Double(0));
row1.add(new Double(1/2.0));
row1.add(new Double(1/2.0));
row1.add(new Double(0));
row1.add(new Double(1/2.0));
List row2 = new ArrayList();
row2.add(new Double(1 / 3.0));
row2.add(new Double(0));
row2.add(new Double(0));
row2.add(new Double(0));
row2.add(new Double(0));
List row3 = new ArrayList();
row3.add(new Double(1 / 3.0));
row3.add(new Double(0));
row3.add(new Double(0));
row3.add(new Double(1));
row3.add(new Double(1 / 2.0));
List row4 = new ArrayList();
row4.add(new Double(1 / 3.0));
row4.add(new Double(0));
row4.add(new Double(0));
row4.add(new Double(0));
row4.add(new Double(0));
List row5 = new ArrayList();
row5.add(new Double(0));
row5.add(new Double(1 / 2.0));
row5.add(new Double(1 / 2.0));
row5.add(new Double(0));
row5.add(new Double(0));
List> s = new ArrayList>();
s.add(row1);
s.add(row2);
s.add(row3);
s.add(row4);
s.add(row5);
return s;
}
/**
* 初始化U矩阵,全1
*
* @return U
*/
public static List> getU() {
List row1 = new ArrayList();
row1.add(new Double(1));
row1.add(new Double(1));
row1.add(new Double(1));
row1.add(new Double(1));
row1.add(new Double(1));
List row2 = new ArrayList();
row2.add(new Double(1));
row2.add(new Double(1));
row2.add(new Double(1));
row2.add(new Double(1));
row2.add(new Double(1));
List row3 = new ArrayList();
row3.add(new Double(1));
row3.add(new Double(1));
row3.add(new Double(1));
row3.add(new Double(1));
row3.add(new Double(1));
List row4 = new ArrayList();
row4.add(new Double(1));
row4.add(new Double(1));
row4.add(new Double(1));
row4.add(new Double(1));
row4.add(new Double(1));
List row5 = new ArrayList();
row5.add(new Double(1));
row5.add(new Double(1));
row5.add(new Double(1));
row5.add(new Double(1));
row5.add(new Double(1));
List> s = new ArrayList>();
s.add(row1);
s.add(row2);
s.add(row3);
s.add(row4);
s.add(row5);
return s;
}
}
运行结果如下:
alpha的值为: 0.85
初始的向量q为:
2.14335103032906, 0.4690253246490811, 0.152093449701467, 2.751926907462932, 2.354654214646654,
初始的矩阵G为:
0.030000000000000006, 0.455, 0.455, 0.030000000000000006, 0.455,
0.31333333333333335, 0.030000000000000006, 0.030000000000000006, 0.030000000000000006, 0.030000000000000006,
0.31333333333333335, 0.030000000000000006, 0.030000000000000006, 0.88, 0.455,
0.31333333333333335, 0.030000000000000006, 0.030000000000000006, 0.030000000000000006, 0.030000000000000006,
0.030000000000000006, 0.455, 0.455, 0.030000000000000006, 0.030000000000000006,
4.887251418383654
3.386500210061385
1.6202642325269005
0.6564210854150941
0.24415455496348265
0.09488083364237077
0.03952368331558996
0.017295374716670576
0.007741886256110822
0.003381687336098358
0.0014192299548542587
5.851975158821074E-4
2.4345907798372686E-4
1.0318512553661415E-4
4.4341960759112595E-5
1.9098212868186317E-5
8.162665677965815E-6
3.4568836720498055E-6
1.4585978458919526E-6
6.168998657103376E-7
2.621451391654222E-7
1.1175579711691102E-7
4.764844675475995E-8
q1:
2.252449030584827, 0.8743254197002868, 2.2892850469941717, 0.8743254197002868, 1.5806660098096288,
q:
2.252449030317913, 0.8743254198027104, 2.2892850807170464, 0.8743254198027104, 1.580665976148821,
PageRank为:
2.252449030317913, 0.8743254198027104, 2.2892850807170464, 0.8743254198027104, 1.580665976148821,