狭义相对论的洛伦兹变换几何推导

      考虑时空中的一条直线，选定一个原点，代表 AB 两点在时空中重叠事件。 A，B 两点相对以速度 u 相对匀速运动。该运动的时空图可以用二维仿射空间表示，对任意质点建立自己在时空中建立仿射坐标系。下面分别建立分别相对 A 静止的和相对 B 静止的两个坐标，分别记为 A 系和 B 系， A 系和 B 系同一时空中的两个不同坐标系。本文分别讨论两个坐标系中， A 的世界线、 B 的世界线和光子的世界线，以求得坐标变换式。

（注：世界线是质点在时空中的运动的描述，在惯性系中静止的质点世界线平行于时间轴；匀速运动或静止的质点世界线为直线，可以用一个矢量代表其世界线的方向。）

---

      为了简化运算，我们假定某个时刻， AB 两个质点重合，以此点为原点建立分别相对于 A、B 两点静止的两个坐标系。假设在某个坐标系下光速为 c ， AB 相对速度为 u ；适当调整单位比如时间取秒，空间单位取光秒，这时光速为1，在该单位下面， AB 相对速度数值为 u/c ,下文中取 v=u/c .

1. 光子、B点的世界线在A系中的表达

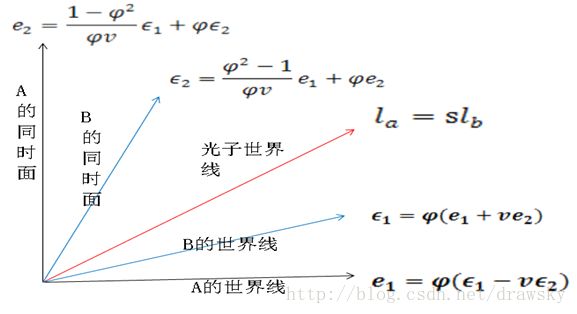
      假定 A 静止，为 A 建立时空坐标基矢。在二维时空中，取一个向量 e1 为时间轴， e2 为 A 的同时面方向（考虑到空间只分析一维，同时面其实是直线）。适当选取不同的时间轴和同时面方向向量，可以使得光线的世界线方向为：

la=e1+e2(1)

在此坐标系下，B的世界线方向为：

Tb=(e1+ve2)

2. 光子、 A 点的世界线在 B 系中的表达

      根据狭义相对性原理，建立B的坐标系应当与A有相同的表达式，做字母替换即可（但是应当注意，选定好速度的方向之后，AB的方向是相反的，v有号差）。

      现在假定 B 系为参考系， B 静止， A 运动，取一个方向 ϵ1 为时间轴， ϵ2 为 B 的同时面方向。
A 系和 B 系对光子世界线方向描述一致：

lb=ϵ1+ϵ2(2)

在此坐标系下， A 的世界线方向为：

Ta=(ϵ1−vϵ2)

3. 相对性原理

      考虑 B 质点的世界线方向，其在 A 坐标系是 Tb ，在 B 的坐标看 ϵ1 ，因此这两个向量方向相同，“长度”相差常数因子为 φ ，有：

φTb=ϵ1=φ(e1+ve2)(3)

同理得到（ 注意，根据相对性原理，坐标表达式应当一致，所以两个方程的常数因子相同，都是φ）：

φTa=e1=φ(ϵ1−vϵ2)(4)

4. 求解基变换矩阵

      联合 (3),(4) ，得到 A 的同时面在 B 系中的表达式：

ϵ1=φ(φ(ϵ1−vϵ2)+ve2)⟹e2=(1−φ2)/φvϵ1+φϵ2(5)

同样有 B 的同时面在 A 系中的表达式：

e1=φ(φ(e1+ve2)−vϵ2)⟹ϵ2=(φ2−1)/φve1+φe2(6)

      考察光子世界线，在 AB 两个坐标系下的表达式分别为 (1),(2) 两式，都表示光子世界线方向，方向应当相同，相差一个常数因子，即：

la=slb=e1+e2=s(ϵ1+ϵ2)

可以得到：

e1+e2=φ(ϵ1−vϵ2)+(1−φ2)/φvϵ1+φϵ2=(φ+(1−φ2)/φv)ϵ1+(φ−φv)ϵ2=s(ϵ1+ϵ2)⇒s=(φ+(1−φ2)/φv)=(φ−φv)⇒φ2(1−v2)=1

所以有 φ=1/1−v2−−−−−√ ， (1−φ2)/φv=φv
由此有基矢变换为：

(e1e2)=11−v2−−−−−√(1vv1)(ϵ1ϵ2)

5. 坐标变换

      在A坐标系中，任意点 xe1+te2 ,在 B 系中表示为： yϵ1+sϵ2 ;则有：

(xt)=11−v2−−−−−√(xt)(1vv1)(ϵ1ϵ2)=(ys)(ϵ1ϵ2)

⇒(ys)=11−v2−−−−−√(xt)(1vv1)

得到：

y=(x+vt)/1−v2−−−−−√，s=(vx+t)/1−v2−−−−−√

取光速为 c ， AB 相对速度为 u ,即 v=u/c 则有变换式如下：

y=x+ut/c1−（u/c)2−−−−−−−−−√

，

s=(ux/c+t)1−（u/c)2−−−−−−−−−√

备注：

      同一时空中涉及到的五个矢量，分别是A的世界线、同时面，B的世界线、同时面，光子的世界线及其之间的关系如下图：