【算法】(扩展)KMP+manacher
今天头脑风暴……然后就爆炸了!
讲字符串,图tm的坑,很难懂,然而还是可以懂。好吧也不是很难懂反正就是这样的。
=========================充满恶趣味的分割线=========================
首先来讲讲KMP这个字符串匹配中常用的方法。由于可查资料太多,不知道怎么说了~~
首先我们给出一个问题:
给出一个长度n的字符串S和一个长度m的字符串T,
问字符串T在S中出现了多少次?
这种方法用暴力来写,枚举开头位循环地找,显然时间复杂度是 O(nm) ,效率很低,而且数据稍大就会爆。那么为什么会这样呢?其实就是因为重复比较。
比如:
S:aaaaaaaaaaaaaaaaaaaaab
T:aaaaaaab
我们可以发现,在比较前面的时候,’a’是可以一直匹配下去的,直到找到T串里的’b’才会知道这次匹配不成功,显然做了很多无谓的匹配。
KMP就是处理重复比较的算法,核心思想是当匹配不成立,从下一个有可能匹配成功的地方开始比较,而不是简单的把开头推后一位。后面讲到的很多关于字符串处理的也与这个思想有关。
我们可以通过对字符串T的处理,处理出一个next数组,即当字符串T在第i位匹配失败,只需要从S的此位开始,与T的next[i]位比较即可,它的原理是:
next[i+1]表示满足 T[0..x]=T[i−x..i] 的最大的 x(0<x<i,不存在x时next[i]=0)
当T串的前i个字符匹配成功的时候,前next[i]个字符必定也是匹配成功
也就是说当T串第i个字符失配的时候,可以从T串的第next[i]个字符重新开始匹配。
那么next数组怎么求呢?这样求好啦~
因为我们看起来是要求在S里匹配T,那我们也可以直接在T里面匹配T~就是这样~跳到可能的位置~
以下代码W是短的字符串,即被匹配字符串。lenW表示W字符串长度
next[0]=next[1]=0;k=0;
for(int i=1;iwhile(k && W[i]!=W[k])
k=next[k];
if(W[i]==W[k])
next[i+1]=++k;
else
next[i+1]=0;
} 我们就可以运用这个next数组来匹配:
S串每匹配一位,就检查T串的下一位能不能匹配,如果不能匹配就跳到T串相应的next位置开始匹配,如此直到可以匹配或者T串被迫从头开始匹配为止。
just like this:
其中T是匹配串……
k=ans=0;
for(int i=0;iwhile(k && T[i]!=W[k])
k=next[k];
if(T[i]==W[k])
++k;
if(k==lenW)
{
++ans;
k=next[k];
}
} 时间复杂度分析:
在算法中,S的匹配位置前进n次,k值因此能够增加n,而通过next数组回退一次,k至少减少1,因此最多回退n次,且前进和回退的耗时均为常数。
因此匹配部分时间复杂度为O(n)
同理可得预处理部分时间复杂度O(m)
总的时间复杂度为O(n+m)
===========================鬼畜的分割线===========================
然后讲了传说中的manacher算法……处理回文串用到的东西哦。
那么问题来了:
挖掘机技术哪家强
给定一个长度为n字符串S,现在要从中找出一个回文的子串T。字符串A是回文的,当且仅当A反转后的A’和A完全相等。问T可能的最大长度。
暴力方法大家都懂的,枚举开始枚举长度一位位搜咯, O(n) 而已嘛~
好吧,其实我首先想到的方法是根据回文串的特性,枚举每个回文串的中点,这样就可以直接往两边找就好啦,时间 O(n2) ,然而遇到偶数长度的回文串并不能处理。
就把它转成奇数就好啦~,在每两个字符之间加一个没出现过的字符,然后再加一头一位两个不同字符作终止,就好啦-.-。
比如原串abba ——> @#a#b#b#a#%
这样就可以啦。要注意找回文串时是可以从’#’开始找的,不需要跳过,这样整个回文串的长度就是找出来的半径减一就好啦(你懂的)。
然而这并不是重点,我们要更快啊!
想到之前的KMP是可以通过已知求未知,我们的manacher算法也是如此,通过先前已经求过的回文串的长度来求当前为中心的最长回文串。
举个栗子:
S: caaabaaaaabaaac
ans:1131713F31? (以该位置为中心的答案)
我们可以通过S[8]中心处的答案得到S[1..15]’=S[1..15],又通过S[5]中心处得到S[2..8]’=S[2..8],我们可以推得S[11]中心处的答案。
即:
∵S[1..15]’=S[1..15]’ ∴S[2..8]’=S[8..14]
∵S[1..15]’=S[1..15]’ ∴S[2..8]=S[8..14]’
又∵S[2..8]=S[2..8]’
∴S[8..14]=S[2..8]’=S[2..8]=S[8..14]’
也就是说S[11]中心处答案至少为7,?>=7
比较S[7]和S[15],发现S[7]!=S[15]
因此?<9,故S[11]中心处的答案是7
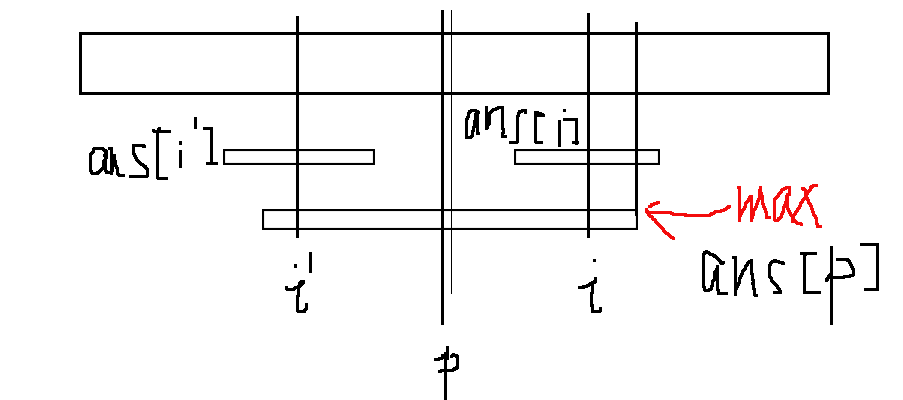
为什么可以这样做呢?实际上是用了回文串的特性,没错就是对称了。我们可以设前面所有找到的回文串中,能延伸最右的回文串其中心下标为p,其回文串长度为ans[p],当前要求点为i,i关于p对称点为i’,当然显然i’=2*p-i。则有两种情况:
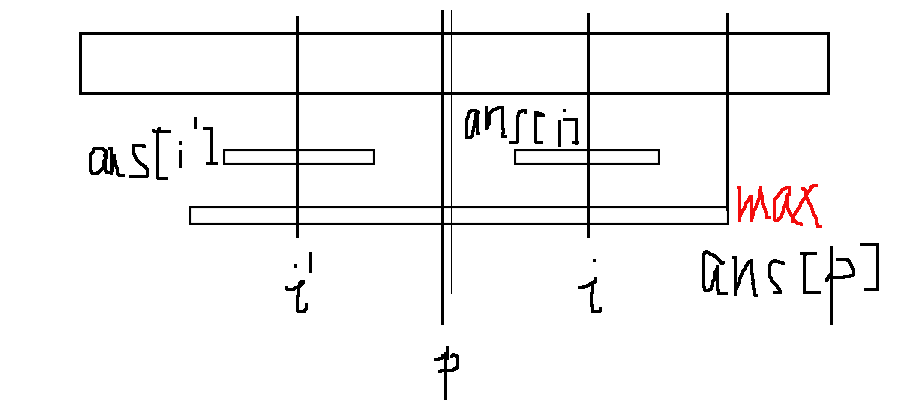
可以看出,此时p+ans[p]大于(等于)i+ans[i],所以以i为中心的回文字串显然是被涵盖在以p为中心的回文字串中的,根据回文串的特性,前面已经求出ans[i’]的值,那么ans[i]=ans[i’]。
此时p+ans[p]小于i+ans[i],所以以i为中心的回文字串显然是不被涵盖在以p为中心的回文字串中的,根据回文串的特性,前面已经求出ans[i’]的值,但我们智能知道[i+i-max..max]这一段是成立的回文串,再往后我们没有依据,所以只能搜索下去。
这就是manacher算法的总体思路。
贴代码咯~
首先你要有一段change,处理偶数情况,当然是都适用的:
void change()
{
len=strlen(S);
for(int i=len-1;i>=0;--i)
{
S[i*2+2]=S[i];
S[i*2+1]='#';
}
S[len*2+1]='#';
S[0]='@';S[len*2+2]='$';
len*=2;
}其中我上面写的len是指不包括两端特殊字符的长度哦~也就是S[1..len]={#a#b#b#..#a#}这样子的。
接下来还要有一段manacher核心代码:
void manacher()
{
memset(ans,0,sizeof(ans));
ans[0]=ans[1]=0;p=1;
for(int i=2;i<=len;++i)
{
ans[i]=max(0, min(ans[2*p-i],p+ans[p]-i) );
while (S[i-ans[i]]==S[i+ans[i]])
ans[i]++;
if(i+ans[i]>p+ans[p])
p=i;
}
realans=0;
for(int i=2;i<=len;++i)
realans=max(ans[i],realans);
printf("%d\n",realans-1);
}时间复杂度:
这个算法while部分每运行一次,p的最右端就向右移动最少一格,然而最右端最多只能移动n格,因此while部分最多执行循环n次,再加上其他部分随着for循环最多执行n次(n均计算字符串被改后的长度),总的时间复杂度为 O(n) 。
好的以上就是manacher算法的内容~
============================偶然来到这个世界的分割线============================
接下来是扩展KMP~还是先丢出一个问题:
给出一个长度n的字符串S[0..n-1],和一个长度m的字符串T[0..n-1],问S的哪个后缀和T具有最长的公共前缀。
暴力显然是 O(nm) 的,但我们要与重复运算作斗争!
首先我们可以试着和kmp一样的思路:
先假设T的每一个后缀T[i..n-1]和T[0..n-1]本身的的最长公共前缀用数组next[i]存储,特别的next[0]=n
然后设答案伸得最远的后缀(不包括原串)为T[p..n-1],如果其公共前缀没有包含字符T[i],就暴力求next[i](i=1时也暴力求),否则可以像manacher一样直接拿现成结果
比如:
S :aaaabaaaa
ans:932104?
已知:S[0..3]=S[5..8]和S[1..3]=S[0..2]
S[0..3]=S[5..8] -> S[1..3]=S[6..8]
故S[6..8]=S[1..3]=S[0..2]
因此ans[6]至少为3
此时我们检查ans[6]能否更大
S[9]!=S[3],因此ans[6]就是3
好吧,由于我自己讲的不算很清,我觉定转载一下哦~
============================以下内容转自ACMer的博客~~============================
拓展KMP算法点这里哦~~~
- 拓展kmp算法一般步骤
通过上面的例子,事实上已经体现了拓展kmp算法的思想,下面来描述拓展kmp算法的一般步骤。
首先我们从左到右依次计算extend数组,在某一时刻,设extend[0…k]已经计算完毕,并且之前匹配过程中所达到的最远位置为P,所谓最远位置,严格来说就是i+extend[i]-1的最大值 (0<=i<=k) ,并且设取这个最大值的位置为po,如在上一个例子中,计算extend[1]时,P=3,po=0。
现在要计算extend[k+1],根据extend数组的定义,可以推断出S[po,P]=T[0,P-po],从而得到 S[k+1,P]=T[k-po+1,P-po],令len=next[k-po+1],(回忆下next数组的定义),分两种情况讨论:
上图中,S[k+1,k+len]=T[0,len-1],然后S[k+len+1]一定不等于T[len],因为如果它们相等,则有S[k+1,k+len+1]=T[k+po+1,k+po+len+1]=T[0,len],那么next[k+po+1]=len+1,这和next数组的定义不符(next[i]表示T[i,m-1]和T的最长公共前缀长度),所以在这种情况下,不用进行任何匹配,就知道extend[k+1]=len。
第二种情况: k+len>=P
如下图:
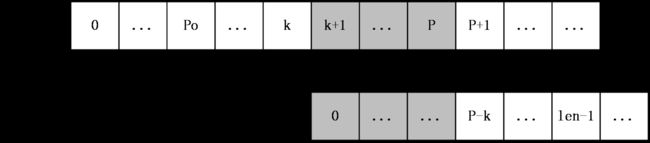
上图中,S[p+1]之后的字符都是未知的,也就是还未进行过匹配的字符串,所以在这种情况下,就要从S[P+1]和T[P-k+1]开始一一匹配,直到发生失配为止,当匹配完成后,如果得到的extend[k+1]+(k+1)大于P则要更新未知P和po。
至此,拓展kmp算法的过程已经描述完成,细心地读者可能会发现,next数组是如何计算还没有进行说明,事实上,计算next数组的过程和计算extend[i]的过程完全一样,将它看成是以T为母串,T为字串的特殊的拓展kmp算法匹配就可以了,计算过程中的next数组全是已经计算过的,所以按照上述介绍的算法计算next数组即可,这里不再赘述。
============================以上内容转自ACMer的博客~~============================
好啦,接下来是贴代码时间哦~
首先是next数组的时间:
void get_NEXT()
{
NEXT[0]=len2;
int i=0,j,p,u;
while(S[i]==S[i+1]&&i+1NEXT[1]=i;
p=1;
for(i=2;iNEXT[p];
if(i+NEXT[i-p]NEXT[i]=NEXT[i-p];
else
{
j=max(NEXT[p]+p-i,0);
while(i+j<len&&S[j]==S[j+i])
j++;
NEXT[i]=j;p=i;
}
}
} 然后是恩主步骤哦~
void EXKMP()
{
int i,j,p,u;
ex[0]=len2;p=0;
for(i=1;i<len;++i)
{
u=p+ex[p];
if(i+NEXT[i-p]NEXT[i-p];
else
{
j=ex[p]+p-i;
if(j<0)j=0;
while(i+j<len&&j 时间复杂度分析:
第一步求next时内层for循环每执行一次,p至少伸长一格,因此内层for循环至多循环m次,加上外层for循环其余语句,可得时间复杂度O(m)
第二步求ex时同理O(n)
总的时间复杂度O(m+n)
完结撒花~~~~