排序算法之归并排序 ( C语言版 )

归并排序 :（Merge Sort）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并, 使用中牺牲空间换取时间的算法 

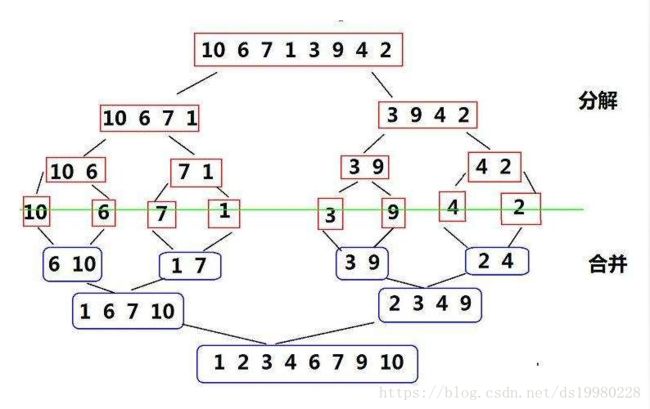
归并算法核心步骤为 : 

• 分解
• 合并

图片来源  ---  https://baike.sogou.com/v8340582.htm?fromTitle=%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F

• 由于归并排序不依赖于待排序元素序列的初始输入状态, 每次划分时两个子序列的长度基本一致, 因此归并排序的最好, 最差好平均时间复杂度均为O(n*log2^n) , 是一种稳定的排序算法
• 归并排序的优化，使用插入排序处理小规模的子数组，一般可以将归并排序的运行时间缩短10%~15%

代码实现如下 : 

//分组归并
void _Merge(int *a, int begin1, int end1, int begin2, int end2, int *tmp)
{
	int index = begin1;
	int i = begin1, j = begin2;
	//注意:当划分的区间足够小时,begin1==end1,begin2==end2
	while (i <= end1&&j <= end2){
		if (a[i]<=a[j])
			tmp[index++] = a[i++];
		else
			tmp[index++] = a[j++];
	}
	//将左边元素填充到tmp中
	while (i <= end1)
		tmp[index++] = a[i++];
	//将右边元素填充的tmp中
	while (j <= end2)
		tmp[index++] = a[j++];
	//将tmp中的数据拷贝到原数组对应的序列区间
	//注意:end2-begin1+1
	memcpy(a + begin1, tmp + begin1, sizeof(int)*(end2 - begin1 + 1));
}
//归并排序
void MergeSort(int *a, int left, int right, int *tmp)
{
	if (left >= right)
		return;
	assert(a);
	//mid将数组二分
	int mid = left + ((right - left) >> 1);
	//左边归并排序,使得左子序列有序
	MergeSort(a, left, mid, tmp);
	//右边归并排序,使得右子序列有序
	MergeSort(a, mid + 1, right, tmp);
	//将两个有序子数组合并
	_Merge(a, left, mid, mid + 1, right, tmp);
}

完整代码 : 

#include 
#include 
#include 
#include 

//分组归并
void _Merge(int *a, int begin1, int end1, int begin2, int end2, int *tmp)
{
	int index = begin1;
	int i = begin1, j = begin2;
	//注意:当划分的区间足够小时,begin1==end1,begin2==end2
	while (i <= end1&&j <= end2){
		if (a[i]<=a[j])
			tmp[index++] = a[i++];
		else
			tmp[index++] = a[j++];
	}
	//将左边元素填充到tmp中
	while (i <= end1)
		tmp[index++] = a[i++];
	//将右边元素填充的tmp中
	while (j <= end2)
		tmp[index++] = a[j++];
	//将tmp中的数据拷贝到原数组对应的序列区间
	//注意:end2-begin1+1
	memcpy(a + begin1, tmp + begin1, sizeof(int)*(end2 - begin1 + 1));
}
//归并排序
void MergeSort(int *a, int left, int right, int *tmp)
{
	if (left >= right)
		return;
	assert(a);
	//mid将数组二分
	int mid = left + ((right - left) >> 1);
	//左边归并排序,使得左子序列有序
	MergeSort(a, left, mid, tmp);
	//右边归并排序,使得右子序列有序
	MergeSort(a, mid + 1, right, tmp);
	//将两个有序子数组合并
	_Merge(a, left, mid, mid + 1, right, tmp);
}
//打印数组
void PrintArray(int *a, int len)
{
	assert(a);
	for (int i = 0; i < len; i++)
		printf("%d ", a[i]);
	printf("\n");
}
int main()
{
	int a[] = { 10, 6, 7, 1, 3, 9, 4, 2 };
	int *tmp = (int *)malloc(sizeof(int)*(sizeof(a) / sizeof(int)));
	memset(tmp, -1, sizeof(a) / sizeof(int));
	MergeSort(a, 0, sizeof(a) / sizeof(int)-1, tmp);
	PrintArray(a, sizeof(a) / sizeof(int));
	system("pause");
	return 0;
}

调试结果如下 :