最短路 （Dijstra）

Problem Description

在每年的校赛里，所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候，却是非常累的！所以现在他们想要寻找最短的从商店到赛场的路线，你可以帮助他们吗？

 

Input

输入包括多组数据。每组数据第一行是两个整数N、M（N<=100，M<=10000），N表示成都的大街上有几个路口，标号为1的路口是商店所在地，标号为N的路口是赛场所在地，M则表示在成都有几条路。N=M=0表示输入结束。接下来M行，每行包括3个整数A，B，C（1<=A,B<=N,1<=C<=1000）,表示在路口A与路口B之间有一条路，我们的工作人员需要C分钟的时间走过这条路。
输入保证至少存在1条商店到赛场的路线。

 

Output

对于每组输入，输出一行，表示工作人员从商店走到赛场的最短时间

 

Sample Input

2 1 1 2 3 3 3 1 2 5 2 3 5 3 1 2 0 0

 

Sample Output

3 2

 

上一波http://acm.hdu.edu.cn/showproblem.php?pid=2544的代码

 

#include 
#include 
#include 
#include 
#include <string>
#include 
#include 
#include 

View Code

 

-----------------------------------------------分隔符----------------------------------------

 做最短路需要注意  点的数据范围 和 优化（附加）  

1.floyd算法的话一般采用 邻接矩阵计算  （矩阵初始化数据不要太大）

 

2.dijkstra算法的话，加上堆优化，也就是优先队列（如果堆加上映射，增加删除操作会更快）

　　适用于在有n个点，m条边的图中，给出起点s，可以求出到达其他每个点的最短路（如果有的话）

 

3.SPFA算法，就暴力广搜松弛，好写好记还挺快，实质是BE优化。 不适用于发散的图，或者网格图之类的 

 

-----------------------------------------------分隔符----------------------------------------

 

运用Dijstra算法思路一般是：

1）最大化路径（最大化主要的作用是筛掉一些不存在的道路）

2）输入存在的路径，初始化所有点为未访问并且将源点到各个点的距离保存到dis[]数组（dis储存源点到各个点的直接距离）

Dijstra核心代码

3）逐个点进行判断，每次找出距离源点的最短距离，并更新该点的状态

4）！！！（敲黑板）

           if( dis[index] + dp[index][j] < dis[j] )
                  dis[j] = dis[index] + dp[index][j];

更新最短的距离

 

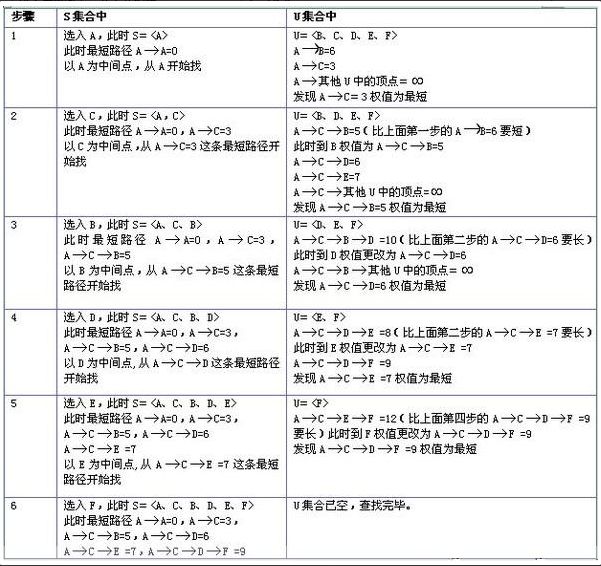
下图结合上面的步骤会更好理解（嘘！！！图是别人的，不要声张）

 

 

 

 

 

 

 

1）去重边
2）堆优化

 Dijstra算法常用于解决单源最短路问题