导电聚合物中热电效应转换原理

CPs中热和电转换原理

绝缘聚合物有共键价原子组成(类似于Si)，$s{p}^3$杂化的碳原子，共享电子被束缚在链形分子的低能量轨道上，导致导电率很低。但是在一些共轭聚合物(conjugated polymers), 比如聚乙炔(trans-polyacetylene), 碳原子$s{p}^2$杂化，在垂直于$\sigma$键的方向形成$\pi$键。由于形成交叠区域，相邻C原子的$s{p}^2$杂化的$p_z$轨道，导致沿着聚合物主体方向，离域电子的移动， 在这种交替的$\sigma$和$\pi$分布的C-atoms中，在激发光谱中，由于Peierls instability， $\pi -band$会被分成$\pi -band(电子填充满)和{\pi }^{\ast }band(无电子)$并有一个能量为$E_g$的gap。与传统的半导体相比，结合的轨道($\pi$)对应于半导体中的价带， 而未结合的轨道 (${\pi }^{\ast }$)对应于半导体中的导带。相似的，在Highest Occupied Molecular Orbital (HOMO) 和 Lowest Unoccupied Molecular Orbital (LUMO)之间的能量$E_g$，类似于半导体中的禁带宽度$E_g$。因此，共轭聚合物的导电率仍然很低，所以说 ，仅靠共轭聚合是不够的，然而，导电率可以通过掺杂增强，但是由于CPs的structure-property relationships，掺杂有副作用。这将在section 4中导论。

1 Electrical conductivity 导电率

一般来说，可以使用电化学或化学方法对聚合物进行掺杂。两种方法处理流程：

• (i) 一个单元结构(monomer)氧化的开始是从$\pi -system$中除去电子，产生一个自由基(free radical)和无自旋的正电荷(spinless positive charge),减少的掺杂剂转化为平衡离子，中和引入到$\pi -electron$系统的正电荷。
• (ii) 电荷与自由基的局部振动引起电荷和自由基的耦合，而这种耦合称为极化(polaron)
• (iii)极化形式可以为自由基阳离子或自由基阴离子(radical cation or radical anion)，在带隙内形成新的局部电子态，低能态被单电子占据，
• (iv)从极化子从除去或添加新的电子会进一步引起新的无旋缺陷，称为双极化，是一个与极化畸变(polaronic distortion)有关的自由基离子对,根据不同的聚合物的化学结构，可以受到其他3到4个单元结构(monomer)的影响。

[22]双极化子的产生在热力学上要比两个极化子的产生更有用，因此，在高的掺杂水平下，两个极化子变为一个双极化子的可能性越大。

其实会联系到半导体中重掺杂下的能级交叠
但是如果掺杂浓度过高，双极化能级会交叠，最终形成连续的带。如下图，并且双极化之间的间隙也会增加因为新形成的双极化子是以牺牲带边为代价而形成的，差杂浓度进一步增加，会导致双极化带的上边界和下边界分别和导带和价带结合，形成类似金属的带[7, 22]

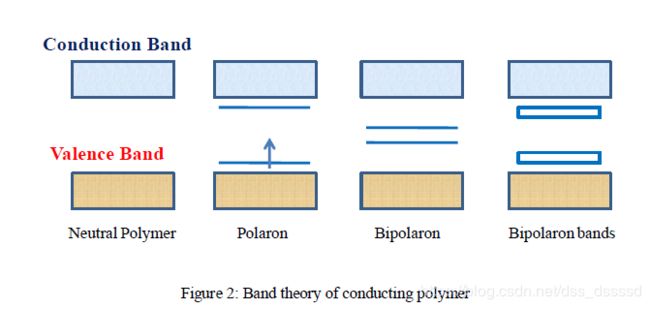
基态退化的共轭聚合物， 比如聚乙炔(polyacetylene)的导电机理可以使用稍微不同的机理解释，由于氧化差杂导致极化子/双极化子的产生 [20-21]。由于基态的退化，带电的阳离子受束缚较弱，可以沿着链自由移动，这种电荷位置相互独立，并隔离基态的两相(自旋相反但能量相同)，称为孤子(soliton)，有时是中性的。例如，
假设聚乙炔产生的孤子可以离域化的距离为12个C-H单元，并且最大的电荷密度与掺杂离子浓度相同。孤子的形成会在带隙之间形成新的局部态，随着掺杂浓度的增加，就像双极化子一样，带电的孤子可会与其他的孤子交叠形成孤子带，最终会与导带/价带接触，导致类似金属的导电性。

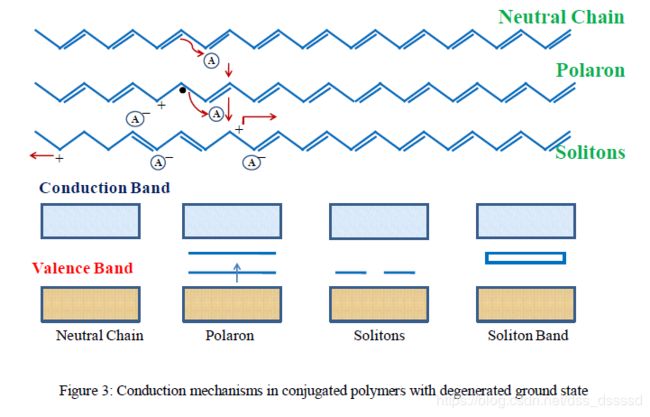
这种导电机理会受到CPs中的能量障碍和空间障碍影响。通过掺杂引入的额外载流子由于与反离子(掺杂剂)的静电吸引而滞留在链中。[27, 86]在低介电常数(~3)中 ，低掺杂会产生大尺寸的陷阱，而这些陷阱会阻碍载流子的移动， 随着掺杂浓度的增加，陷阱会交叠，他们之间的能量势垒会降低。这种在$\pi -轨道$上能量势垒的降低会增强电子移动[11].通过增加差杂浓度实现，然而，空间障碍也会在原子核微观尺度上影响你电荷传输，比如counter ions position,interchain distance, configuration of chains, size of crystalline and amorphous domains, orientation of crystallite。

在CPs中，电子传输是通过跳动过程(hopping process[2, 11-12])实现的,在非掺杂或低掺杂聚合物中， 在外电场作用下，极化子会跳跃到临近的聚合物链的中性区域，
另一方面，在掺杂聚合物中，载流子(一对极化子和反离子)从一个极化子位点跳到另一个极化子位点，而构成跳跃位点的聚合物链不发生任何畸变。在无序或非晶的CPs中，温度与导电率的关系使用VRH模型描述(variable range hopping),假设 constant density of states（定态密度）。
根据VRH模型， 温度与导电率的关系如下:
$$\sigma (T)=\sigma (0)exp(\lfloor -(T_0/T{)}^{\lambda }\rfloor )$$

$T_0$为莫特温度值，
$$T_0=\frac{18}{L{}_c^{3}N(E_F)K_B}$$
$L_c$为定域长度， $N(E_F)$为费米能级的态密度，$K_B$为玻尔兹曼常数。

适度掺杂和结构有序的CPs， 随着链之间定域长度的增加，链之间的连接性更好，会导致很好的电转移特性，
例如，高掺杂和高有序的CPs，比如樟脑磺酸掺杂的PANI(聚苯胺),在低温下表现很好的金属温度依赖性。

2 seebeck cofficient 塞贝克系数

塞贝克系数是开环电压(温度热端和冷端两端之间的电压 )和温差之比，塞贝克系数有三种不同的贡献因子：电子(electronic) 声子(phonon)和电-声子(electron-phonon),在金属系统中存在大量的自由电子，电子主要贡献塞贝克系数。电子从热端移动到 冷端形成电势，产生电子贡献。在这种情况下，塞贝克系数与温差成线性关系[14]
声子贡献主要认为声子曳引效应(Phonon drag), 一般在低温(<200k)比较明显，在低温时声子平均自由程(phonon mean free path)比较大[7]。当声子和电子的平均自由程可比拟时，电子-声子散射变得重要[7, 11].好的晶体结构的高导电聚合物在低温时有较好的电子-声子散射[11, 12]。重掺杂的聚合物，比如polyacetylene(聚乙炔),polyaniline(聚苯胺),polypyrrole (聚吡咯)存在很小的正塞贝克系数($<14uV/K$在接近室温时)，并且随温度有线性下降[7]。然而，由于电子-声子作用可能会导致线性偏差。在轻掺杂的情况下，塞贝克系数要大于重掺杂[7, 12]，对于这种CPs，塞贝克系数随着温度可能非线性增加或降低。有时， 塞贝克系数非线性随着$T^{1/2}$非线性下降，这可以用局部状态之间的莫特变化范围跳变传输解释。局部状态内最邻近跳跃使得塞贝克系数与温度有$1/T$的依赖关系，但是在重掺杂下，塞贝克系数随着温度线性增加[12, 24]

3 Thermal conductivity 热导率

在无机材料中，热导率中的电子部分与电导率耦合，而在有机材料中，由于更强的电荷-晶格耦合效应，这种协同效应无效（违反了Wiedemann-Franz law）。除此之外，由于与无机材料 相比，有机材料的电导率更低,因而电子对$\kappa$的贡献更低[16, 17]。在有机材料中，热传导主要依靠声子(phonon)（比如，量子晶格振动）实现而不是电荷载流子(例如 ${\kappa }_l>{\kappa }_e$)。对于CPs，$\kappa$不仅依赖于分子的重量和形状，还依赖于链结构的不同。对于聚合物的主要链状结构：

• Linear polymers
• Branch polymers
• Crosslinked polymers
• Network polymers
  如下图(a)：
  

聚合物链有多种结构，结合会形成非晶(amorphous)或半晶结构(semi-crystalline), 如上图(b)。不同的结构在热导率和热扩散上有各向异性[18-19]， 对于一个特定的CP，在更有序的链上，各向异性更明显。

尽管这种各向异性(anisotropy)是排列整齐，有序的聚合物链的特点，但是在非晶结构上也存在。这可以解释为热传输机制在两个方向上不同[18]。平面内导热系数值高于横向导热系数，这是由于在聚合物链上的强C-C共价键作用，而不是通过垂直方向上的弱范德华分子相互作用传递热能。如下图：

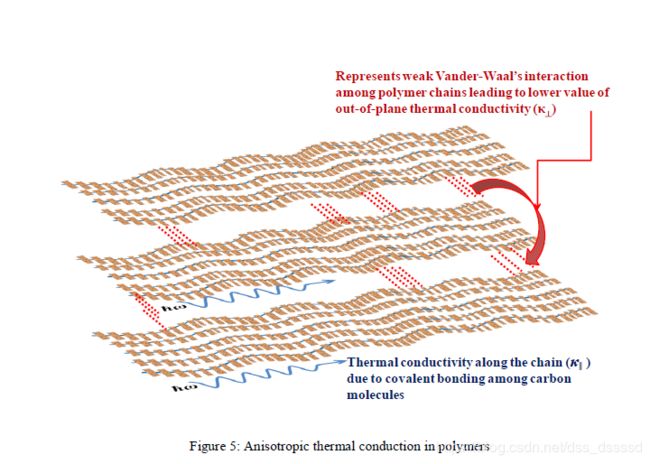
机械形变(在拉伸力作用下)和沉积到基板上的不同方式(spin coatinng, screen printing)也可以将热传输的各向异性引入到聚合物材料中.旋涂过程中的离心力导致平面内和平面间导热性的不同[18]。值得注意的是，对于大多数CPs，即使$\sigma$可以有三个数量级的增加，$\kappa$的变化也很小(比如， 从0.1W/mK到1.0W/mK)。由于CPs的$\kappa$很小，所以测量过程更复杂。同时，导热率的各向异性需要考虑在内[18, 19]。当$\sigma$增加（>=100S/cm）时，也会导致${\kappa }_e$的增加，当${\kappa }_e$可以与${\kappa }_l$相比拟甚至超出时，在估计热导率的时候也要考虑${\kappa }_e$了[11]。$\kappa$与CPs的结晶程度也有关系， 比如在低结晶的CPs中，热导率单调增加；而对于高结晶CPs，热导率很高，随着温度升高（up to 100k）先增加后减小。低温时热导率的偶然上升可以解释为声子-声子散射的抑制导致了声子平均自由增加[11]。