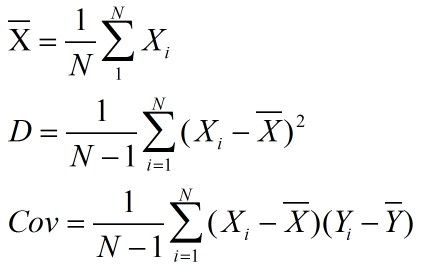numpy中的协方差，方差相关计算
由协方差矩阵计算方差矩阵：
协方差矩阵，求相关矩阵
假设协方差矩阵sigma：
>>> import numpy as np
>>> sigma=np.array([[4,1,2],[2,3,4],[2,3,5]])
>>> print sigma
[[4 1 2]
[2 3 4]
[2 3 5]]
>>> sigma
array([[4, 1, 2],
[2, 3, 4],
[2, 3, 5]])
得出协方差的长度
>>> p=len(sigma)
>>> p
3
得出同等长度的单位矩阵
>>> e=np.eye(p)
>>> e
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
得出协方差矩阵的对角线元素，即方差矩阵
>>> variance=e*sigma
>>> variance
array([[ 4., 0., 0.],
[ 0., 3., 0.],
[ 0., 0., 5.]])
得出标准差矩阵
>>> v=np.power(variance,0.5)
>>> v
array([[ 2. , 0. , 0. ],
[ 0. , 1.73205081, 0. ],
[ 0. , 0. , 2.23606798]])
得出标准差的逆矩阵
>>> I=np.linalg.inv(v)
>>> I
array([[ 0.5 , 0. , 0. ],
[ 0. , 0.57735027, 0. ],
[ 0. , 0. , 0.4472136 ]])
得出相关系数矩阵
>>> cov=I.dot(sigma).dot(I)
>>> cov
array([[ 1. , 0.28867513, 0.4472136 ],
[ 0.57735027, 1. , 1.03279556],
[ 0.4472136 , 0.77459667, 1. ]])
>>>
计算矩阵的方差
在数学中，每一维度指的是列，但是在array中，每一维度指的是一个array。举个例子：
a = array([1,2,3])
a的维度指的是array([1,2,3])，是一维的
在数学中，[1,2,3]维度是三维的。
计算方差的公式为：
>>> from numpy import *
>>> a=array([1,2,7])
>>> a.var()
6.8888888888888884
- 这里计算的方差不是如方差公式那样除以N-1,在numpy里var()表示的是这个公式
