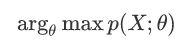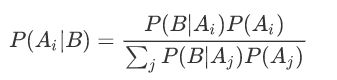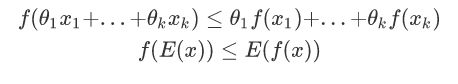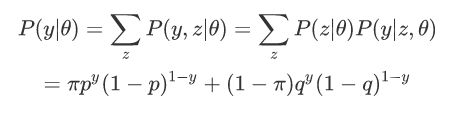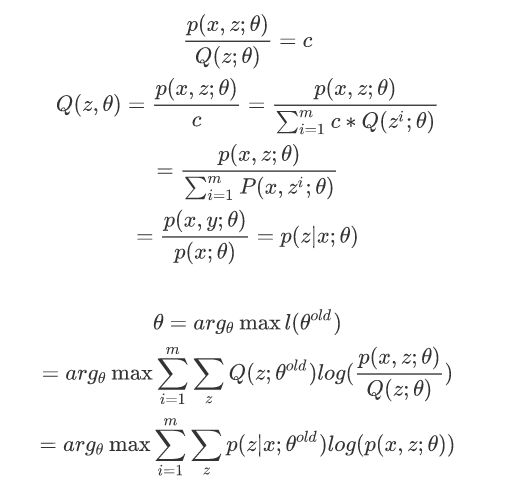最大期望算法
EM算法的正式提出来自美国数学家Arthur Dempster、Nan Laird和Donald Rubin,其在1977年发表的研究对先前出现的作为特例的EM算法进行了总结并给出了标准算法的计算步骤,EM算法也由此被称为Dempster-Laird-Rubin算法。1983年,美国数学家吴建福(C.F. Jeff Wu)给出了EM算法在指数族分布以外的收敛性证明。
MLE
MLE就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值 的计算过程。直白来讲,就是给定了一定的数据,假定知道数据是从某种分布中 随机抽取出来的,但是不知道这个分布具体的参数值,即“模型已定,参数未 知” ,MLE就可以用来估计模型的参数。MLE的目标是找出一组参数(模型中的 参数),使得模型产出观察数据的概率最大。
-
编写似然函数(即联合概率函数)
-
对似然函数取对数,并整理;(一般都进行)
-
求导数;
-
解似然方程。
贝叶斯
贝叶斯算法估计是一种从先验概率和样本分布情况来计算后验概率的一种方式。
贝叶斯算法中的常见概念:P(A)是事件A的先验概率或者边缘概率;P(A|B)是已知B发生后A发生的条件概率,也称为A的后验概率;P(B|A)是已知A发生后B发生的条件概率,也称为B的后验概率;P(B)是事件B的先验概率或者边缘概率。贝叶斯算法估计:
在实际应用中计算:
MAP
MAP和MLE一样,都是通过样本估计参数θ的值;在MLE中,是使似然函数P(x|θ)最大的时候参数θ的值,MLE中假设先验概率是一个等值的;而在MAP中,则是求θ使P(x|θ)P(θ)的值最大,这也就是要求θ值不仅仅是让似然函数最大,同时要求θ本身出现的先验概率也得比较大。
MAP是贝叶斯的一种应用:
Jensen不等式
如果函数为凸函数,那么下面的式子将成立:

如果θ1,....,θk>=0,θ1,....,θk=1将存在:
对于f(E(x))=E(f(x))相等的时候,也就是x==y的时候.
相反对于这样的函数:

公式将变成:
EM算法引入
假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别是π,p和q。进行如下掷硬币试验:先掷硬币A,根据其结果选出硬币B或硬币C,正面选硬币B,反面选硬币C;然后掷选出的硬币,掷硬币的结果,出现正面记作1,出现反面记作0;独立地重复n次试验(这里,n=10),观测结果为1,1,0,1,0,0,1,0,1,1
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币各自的正面朝上的概率,即三硬币模型的参数。
这里,随机变量y是观测变量,表示一次试验观测的结果是1或0;随机变量z是隐变量,表示未观测到的掷硬币A的结果;θ=(π,p,q)是模型参数。随机变量y的数据可以观测,随机变量z的数据不可观测。
三硬币模型:
EM算法(Expectation Maximization Algorithm, 最大期望算法)是一种迭代类型的算法,是一种在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐藏变量。
EM原理
给定的m个训练样本{x(1),x(2),...,x(m)},样本间独立,找出样本的模型参数θ,极大化模型分布的对数似然函数如下:
假定样本数据中存在隐含数据z={z(1),z(2),...,z(k)},此时极大化模型分布的对数似然函数如下:
令z的分布为Q(z;θ) ,并且Q(z;θ)≥0;sum(Q(z;θ))=1;那么有如下公式:
求l(θ)的最大值而后面的式子正好是它的下界,所以求后面式子的上界就行了,根据jensen不等式,当下列式子为常数的时候,l(θ)才能取等号,
EM算法的流程
样本数据x={x,x,...,x},联合分布p(x,z;θ),条件分布p(z|x;θ),最大迭代次数J1) 随机初始化模型参数θ的初始值θ02) 开始EM算法的迭代处理:
-
E步:计算联合分布的条件概率期望
-
M步:极大化L函数,得到θj+1
-
如果θj+1已经收敛,则算法结束,输出最终的模型参数θ,否则继续迭代处理
给出停止迭代的条件,一般是对较小的正数ε1,ε2,若满足下面条件则停止迭代
现在回到刚开始算法引入时候三个硬币例子:
1,初始化模型参数π,p,q
2,EM迭代:
E:估计隐藏变量概率分布期望函数
M:根据期望函数重新估计分布函数的参数π,p,q
对上面的式子求偏导即可: