数字图像处理第六章 ——彩色图像处理（下）

数字图像处理—彩色图像处理

（五） 彩色图像的空间滤波

彩色图像滤波的目标就是同时达到三个目的：削弱噪声，保护色调和保护边缘或细节信息。下面主要讨论的就是彩色图像的平滑处理和锐化处理。

5.1 彩色图像的平滑处理

平滑单色图像的一种方法是定义相应的系数是 1 的模板，用空间模板的系数去乘所有像素的值，并用模板中元素的总数去除。用空间掩膜平滑来处理彩色图像，该处理用处理灰度图像的相同方法来表达，只是代替单个像素。

令 Sxy表示彩色图像中以(x,y)为中心的邻域的一组坐标。在该邻域中，RGB向量的平均值是：

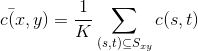
其中，K 是邻域中像素点的数量。附加向量的特性是：

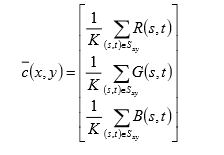
该向量的每个分量都作为将要得到的结果，结果是用每个分量图像执 邻域平均获得的，使用的是上边提到的滤波器模板。因此，得出这样的结论：用邻域平均的平滑可以在每个图像平面的基础上执行。如果邻域平均直接在彩色向量空间执行，那么结果是相同的。

概念上，平滑 RGB彩色图像fc时，线性空间滤波由下面的步骤组成：

1.抽取 3 个分量图像：

fR= I(:,:,1);
fG = I(:,:,2);
fB = I(:,:,3);

2.分别过滤每个分量图像。例如，令w = fspecial(‘average’, 25)表示用fspecial产生的平滑滤波器，平滑分量图像：

fR_filtered = imfilter(fR, w, ‘replicate’);
fG__filtered = imfilter(fG, w, ‘replicate’);
fB_filtered = imfilter(fB, w, ‘replicate’);

也可以对这三个图像分量一起处理：

fc_filtered = imfilter(I, w, ‘replicate’);

3.重建滤波过的 RGB图像：

fc_filtered = cat(3, fR_filtered, fG_filtered, fB_filtered)

因为可以在 MATLAB中使用与单色图像相同的语法来执行 RGB图像的线性滤波， 所以可以把前三步合并为一步：

fc_filtered = imfilter(fc, w, ‘replicate’);

编写代码：

rgb_image=imread('D:\数字图像处理\第六章学习\flower6.tif');       %加载彩色图像
fR = rgb_image(:, :, 1);       %提取R通道分量图像
fG = rgb_image(:, :, 2);       %提取G通道分量图像
fB = rgb_image(:, :, 3);       %提取B通道分量图像
subplot(2, 2, 1), imshow(rgb_image);title('(a)原图像');
subplot(2, 2, 2), imshow(fR);title('(b)红色分量图');
subplot(2, 2, 3), imshow(fG);title('(c) 绿色分量图');
subplot(2, 2, 4), imshow(fB) ;title('(d)蓝色分量图');  

代码运行效果如下：

接下来，用尺寸为 25×25 像素的相同滤波器滤波亮度分量。平均滤波器已足够大，可以产生有意义的模糊度。选择这个尺寸的滤波器，是为了演示在 RGB 空间中进行平滑处理的效果，与在 RGB 空间被变换到 HSI 空间后，只使用图像的亮度分量达到类似结果之间的不同之处。

编写代码：

rgb_image=imread('D:\数字图像处理\第六章学习\flower6.tif');
fR = rgb_image(:, :, 1);
fG = rgb_image(:, :, 2);
fB = rgb_image(:, :, 3);
w = fspecial('average', 25);
fR_filtered = imfilter(fR, w, 'replicate');      %平滑红色分量图像
fG_filtered = imfilter(fG, w, 'replicate');      %平滑绿色分量图像 
fB_filtered = imfilter(fB, w, 'replicate');      %平滑蓝色分量图像
fc_filtered = cat(3,fR_filtered,fG_filtered,fB_filtered);   %将这四个句子可以改为：fc_filtered = imfilter(f, w, 'replicate');
subplot(1,2,1);imshow(rgb_image);title('(a)RGB图像');
subplot(1,2,2);imshow(fc_filtered,'Border','tight');title('(b)平滑 R、G、B 图像平面得到的 RGB 图像');

代码运行效果如下：

编写代码：

fc=imread('D:\数字图像处理\第六章学习\flower6.tif');
h = rgb2hsi(fc);
H = h(:, :, 1);
S = h(:, :, 2);
I = h(:, :, 3);
w = fspecial('average', 25);
I_filtered = imfilter(I, w, 'replicate');
h=cat(3,H,S,I_filtered);      %cat函数是拼接数组的函数，这里将在第3维上进行拼接。
f=hsi2rgb(h);                      
subplot(1,2,1);imshow(fc);title('(c)RGB图像');
subplot(1,2,2);imshow(f);title('(d)仅对HIS相等图像的亮度分量进行平滑的结果');

代码运行效果如下：


编写代码：

fc=imread('D:\数字图像处理\第六章学习\flower6.tif');
h = rgb2hsi(fc);
H = h(:, :, 1);
S = h(:, :, 2);
I = h(:, :, 3);
w = fspecial('average', 25);
H_filtered = imfilter(H, w, 'replicate');
S_filtered = imfilter(S, w, 'replicate');
I_filtered = imfilter(I, w, 'replicate');
h=cat(3,H_filtered,S_filtered,I_filtered);   %构造多维数组，即合并3分量图像为一副彩色图像
f=hsi2rgb(h);
subplot(1,2,1);imshow(fc);title('(e)RGB图像');
subplot(1,2,2);imshow(f);title('(f)平滑所有三个 HIS 分量的结果 ');

代码运行效果如下：


实验总结：

显然，滤波后的两种结果不同。例如，除图像有点模糊以外，图 (d)中花朵顶部出现模糊的绿色边缘。原因是通过平滑处理，亮度分量值的变化减少了，但色调和饱和度分量没有变化。合乎逻辑的情况是用相同的滤波器去平滑所有的三个 HSI 分量，然而，这将改变色调和饱和度值之间的相对关系，这样会产生无意义的结果，如图 (f)所示。特别是在这幅图像中，图像中围绕着花朵的较亮绿色边缘，还有围绕着中心黄色区域的边界，这个效果也是十分明显的。 一般来说，当模板的尺寸减小时，对 RGB 分量图像进行滤波和对同一图像的 HSI 亮度分量进行滤波时，得到的差别也减少了，这一点可以从小女孩图像看出。

5.2 彩色图像的锐化处理

在图像增强中，平滑是为了消除图像中噪声的干扰，或者降低对比度，与之相反，有时为了强调图像的边缘和细节，需要对图像进行锐化，提高对比度。

预备知识：

拉普拉斯锐化图像是根据图像某个像素的周围像素到此像素的突变程度有关，也就是说它的依据是图像像素的变化程度。当邻域中心像素灰度低于它所在的领域内其它像素的平均灰度时，此中心像素的灰度应被进一步降低，当邻域中心像素灰度高于它所在的邻域内其它像素的平均灰度时，此中心像素的灰度应被进一步提高，以此实现图像的锐化处理。

一个函数的一阶微分描述了函数图像是朝哪里变化的，即增长或者降低；而二阶微分描述的则是图像变化的速度，急剧增长下降还是平缓的增长下降。那么据此我们可以猜测出依据二阶微分能够找到图像的色素的过渡程度，例如白色到黑色的过渡就是比较急剧的。

首先推导二阶微分与像素的关系，先看一阶偏微分和推出的二元函数微分：

一阶微分法能够用来检测边缘是否存在。那么二阶微分法，也就是拉普拉斯算子就可以确定边缘的位置。

这样可以找到一个模板矩阵：

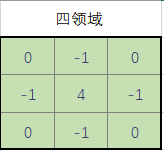
这个四邻域对应上面的二阶微分法

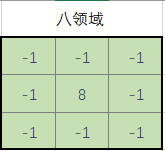
八领域的表示法为：

从上面的两种模板中就可以看出，如果一个黑色平面中有一个白点，那么模板矩阵可以使这个白点更亮。由于图像边缘就是灰度发生跳变的区域，所以拉普拉斯模板对边缘检测很有用。

将算得的值替换原(x,y)处的像素值，可以得到类似边界的地方，然后根据下式得到锐化图像：

编写代码：

%拉普拉斯算子锐化图像，用二阶微分
%四邻接g(x,y)=[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)
I1=imread('D:\数字图像处理\第六章学习\jimei2.png');
I=im2double(I1);
[m,n,c]=size(I);
A=zeros(m,n,c);
%分别处理R、G、B
%先对R进行处理
for i=2:m-1
    for j=2:n-1
        A(i,j,1)=I(i+1,j,1)+I(i-1,j,1)+I(i,j+1,1)+I(i,j-1,1)-4*I(i,j,1);
    end
end

%再对G进行处理
for i=2:m-1
    for j=2:n-1
        A(i,j,2)=I(i+1,j,2)+I(i-1,j,2)+I(i,j+1,2)+I(i,j-1,2)-4*I(i,j,2);
    end
end

%最后对B进行处理
for i=2:m-1
    for j=2:n-1
        A(i,j,3)=I(i+1,j,3)+I(i-1,j,3)+I(i,j+1,3)+I(i,j-1,3)-4*I(i,j,3);
    end
end
B=I-A;

 imwrite(B,'jimei3.png','png');
 imshow('D:\数字图像处理\第六章学习\jimei2.png');title('不清晰图像');figure
 imshow('jimei3.png');title('得到的清晰图像')

代码运行效果如下：

实验总结：

从图像可以看出，拉普拉斯锐化模板在边缘检测中很有用，图像边缘变得非常清晰，对比度明显，细节部分有所增强，不管是荷叶，建筑物，小亭子，蓝色的天空背景都比原图要更亮一点，可以验证拉普拉斯锐化图像原理，当邻域中心像素灰度低于它所在的领域内其它像素的平均灰度时，此中心像素的灰度应被进一步降低，当邻域中心像素灰度高于它所在的邻域内其它像素的平均灰度时，此中心像素的灰度应被进一步提高，以此实现图像的锐化处理。

根据课本，从向量分析中，知道向量的拉普拉斯被定义为矢量，它们的分量等于输入向量的分量的拉普拉斯。在 RGB彩色系统中，引入的矢量 c 的拉普拉斯是：

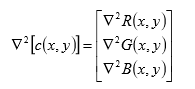
这说明，可以通过分别计算每个分量图像的拉普拉斯来计算全彩图像的拉普拉斯。

编写代码：

fb=imread('D:\数字图像处理\第六章学习\flower7.tif');
lapmask = [1 1 1;1 -8 1;1 1 1];    %拉普拉斯算子
fb = tofloat(fb);
fen = fb - imfilter(fb, lapmask, 'replicate');
subplot(2, 2, 1), imshow(fb);title('(a)模糊图像');
subplot(2, 2, 2), imshow(fen);title('(b)用拉普拉斯增强图像');

代码运行效果如下：

图(a)显示了稍微有点模糊的图，为了锐化这幅图像，使用拉普拉斯滤波模板，对RGB 图像直接用imfilter滤波，图 (b)显示了结果，图像在锐度特性上的显著加强，比如水滴、叶子上的纹路、花朵黄色的中心和前景中明显的绿色植物。

（六） 直接在 RGB 矢量空间中处理

基于单独彩色平面的处理不等于直接在 RGB矢量空间中进行的计算。下面通过考虑彩色图像处理的两个重要应用来说明矢量处理：彩色边缘检测和区域分割。

6.1 使用梯度的彩色边缘检测

2D函数 f(x,y)的梯度定义为如下矢量：

这个矢量的大小是：

通常，这个数量用绝对值来近似：

这个近似值避免了平方和开方计算，但是仍然具有推导过的特性(例如在常数区域为 0，在 像素值变化的区域，幅度与变化程度成比例)。在通常的应用中，把梯度的幅值简单地作为梯度。

梯度向量的基本特性是在 f 坐标(x, y)处指向最大变化率的方向。最大变化率发生的角度是：

按照惯例，这个导数用在一幅图像中某个小邻域内像素值的差来近似。下图显示了 3×3 大小的邻域，这里的 z 代表亮度值。在区域中心点 x方向上(垂直)的偏微分的近似由下边的差给出：




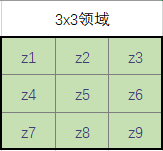
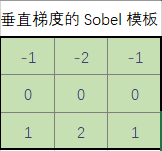
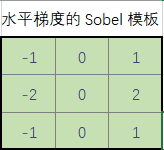
类似的，y 方向上的微分由下面的差近似：

此刻，主要讨论是在 RGB 彩色空间中计算梯度。然而，刚刚推导的方法可应用于 2D空间，但是不能扩展到高维空间。将之运用到 RGB图像的唯一方法是计算每个彩色图像分量的梯度，然后合并结果。遗憾的是，这与直接在 RGB向量空间中计算边缘是不同的。问题是定义过的向量 c 的梯度。下面是可选的各种方法之一，在这里，梯度的概念可延伸到向量函数。

令r、g和b是 RGB彩色空间沿 R、G、B 轴的单位矢量，定义矢量：

和

根据这些矢量的点积，定义 gxx、gyy和 gxy：


和

记住 R、G 和 B，因而 g 是 x 和 y 的函数。使用这种符号，可以说明——c(x,y)的最大变化率方向将作为(x,y)函数由角度给出：

并且在该方向上，由 θ(x,y)给出的变化率的值(例如梯度值)由下式给出：

数组θ(x,y)和$F_{\theta }$(x,y)是与输入图像尺寸相同的图像。θ(x,y)的元素是用于计算梯度的每个
点的角度，并且$F_{\theta }$(x,y)是梯度图像。

使用梯度的彩色边缘检测，目的是标识数字图像中亮度变化明显的点。下面的函数用来计算彩色图像的梯度：

[VG,A,PPG] = colorgrad(f,T)

其中， f是 RGB图像， T是[0,1]范围内的阈值选项(默认为 0)；VG是 RGB向量梯度 Fθ(x, y)； A 是以弧度计的角度 θ(x, y)，并且 PPG 是由单独彩色平面的 2D 梯度之和形成的梯度图像。

代码编写：

fc=imread('D:\数字图像处理\第六章学习\sun.jpg');
[VG,A,PPG]=colorgrad(fc,0.5);%VG为向量梯度，A为向量角度，PPG为计算每一维梯度后合成  
subplot(2, 2, 1), imshow(fc);title('(a)原图像');
subplot(2, 2, 2), imshow(VG);title('(b)T=0.5,在rgb空间计算梯度图像');
subplot(2, 2, 3), imshow(PPG);title('(c)T=0.5,分别在rgb计算梯度然后相加');
subplot(2, 2, 4), imshow(abs(VG-PPG),[]);title('(d)T=0.5,2种梯度的绝对值');   

代码运行效果如下：

向日葵图像分别在T=0,T=0.5,T=1时的图像：

夜晚建筑物图像分别在T=0,T=0.5,T=1时的图像：

带亮点小孩人脸图像分别在T=0,T=0.5,T=1时的图像：

实验总结：

对于同一张图的不同处理，T值越小能够检测的边线越多，越容易从图像中挑出不相关信息；T越大，会丢失细的或者短的线条，当T=0时检测的边线最多，当T=1时，几乎检测不到边线，图像为纯黑色。通过合并单独彩色平面的梯度来计算彩色图像的梯度，与直接在 RGB 向量空间中计算梯度得到的效果也是不同的；直接在 RGB 向量空间中计算梯度得到的图像效果要好一点，边线更多；两种梯度的绝对差检测的边线最少。对于不同的图像，在同样的T值情况下，图像清晰，边缘界限明显，颜色对比度大的图像检测到的边线会更多（例如向日葵图像），图像整体偏暗，边缘分界线不明显的图像检测到的边线相对少一点（例如夜晚建筑物图像），当T值越来越大时，所有图像检测的边线会越来越少，但是图像中含有明显黑白对比度大的部分，白色部分边线会更清晰的检测出来，算法在这方面优势更明显（例如小孩头发上的亮点线）。

6.2 在 RGB向量空间中分割图像

分割的目的是对图像中的每个 RGB 像素进行分类，使之在指定的范围内有或没有一种颜色。为了执行这 一比较，拥有相似性度量是必要的。最简单的度量之一是欧几里德距离。令 z表示 RGB空间的任意点。如果它们之间的距离小于指定的阈值 T，那么 z 相似于 m。z 和 m 之间的欧几里德距 离由下式给出：

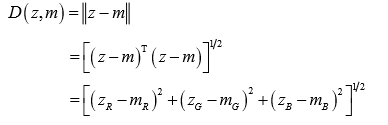
在这里，||.||是参量的范数，并且下标 R、G、B 表示向量 m 和 z 的 RGB 分量。点的轨迹 D(z,m)≤T是半径为 T的球，根据定义，包括在球的内部或表面 的点满足特定的彩色准则，球外部的点则不满足。在图像中对这两组点编码，比如黑的和白的， 将会产生分割的二值图像。上述方程的有用归纳是距离度量形式：

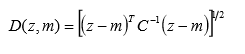
在刚才描述的方法中，分割通过函数colorseg实现，语法如下：

S = colorseg(method, f, T, parameters)

在这里，method 不是’euclidean’就是’mahalanobis’，f 是待分割的 RGB 彩色图
像， T是前边描述的阈值。如果选择’eucliden’，输入参量将是m，如果选择’mahalanobis’， 将是m和c。参数m是均值 m， c是协方差矩阵 C。输出S 是二值图像(和原始图像的大小相同)， 包括 0s。阈值测试失败的点为 0，通过阈值测试的点为 1。1 表示基于彩色内容从f 分割出的区域。

预备知识：

马氏距离：马氏距离(Mahalanobis distance)表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是，它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的），并且是尺度无关的，即独立于测量尺度。
对于一个均值为协方差矩阵为∑的多变量向量其马氏距离为

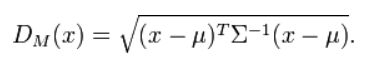
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量x与y的差异程度:

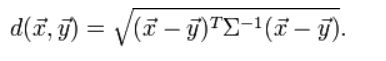
如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧式距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离’.

欧式距离：最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中，如点 x = (x1,…,xn) 和 y = (y1,…,yn) 之间的距离为：

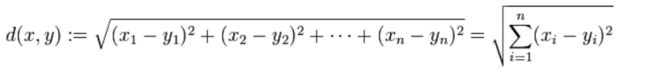
欧氏距离虽然很有用，但也有明显的缺点。它将样品的不同属性（即各指标或各变量量纲）之间的差别等同看待，这一点有时不能满足实际要求。例如，在教育研究中，经常遇到对人的分析和判别，个体的不同属性对于区分个体有着不同的重要性。因此，欧氏距离适用于向量各分量的度量标准统一的情况。

RGB彩色图像分割

编写代码：

f = imread('D:\数字图像处理\第六章学习\sun.jpg');
imshow(f);
title('原图像');
figure,mask=roipoly(f);%roipoly为选择感兴趣的多边形
red=immultiply(mask,f(:,:,1));%immultipy函数为2幅图像对应的元素相乘
green=immultiply(mask,f(:,:,2));
blue=immultiply(mask,f(:,:,3));
g=cat(3,red,green,blue);%将对应的3个分量重新组合
figure,imshow(g);title('用函数roipoly交互式地提取感兴趣的区域');

代码运行效果如下：

编写代码：

f = imread('D:\数字图像处理\第六章学习\girl.png');
imshow(f);
title('原图像');
figure,mask=roipoly(f);%roipoly为选择感兴趣的多边形
red=immultiply(mask,f(:,:,1));%immultipy函数为2幅图像对应的元素相乘
green=immultiply(mask,f(:,:,2));
blue=immultiply(mask,f(:,:,3));
g=cat(3,red,green,blue);%将对应的3个分量重新组合
figure,imshow(g);title('用函数roipoly交互式地提取感兴趣的区域');
[M,N,K]=size(g);%这里k为3
I=reshape(g,M*N,3);%I为M*N行，3列的数组
idx=find(mask);
I=double(I(idx,1:3));
[C,m]=covmatrix(I);%计算出协方差矩阵C和均值m
d=diag(C);%方差
sd=sqrt(d);%标准差

E25=colorseg('euclidean',f,25,m);%使用欧式距离进行彩色分割
figure,subplot(2,2,1),imshow(E25);
title('(a)使用euclidean,T=25分割效果');

E50=colorseg('euclidean',f,50,m);
subplot(2,2,2),imshow(E50);
title('(b)使用euclidean,T=50分割效果');

E75=colorseg('euclidean',f,75,m);
subplot(2,2,3),imshow(E75);
title('(c)使用euclidean,T=75分割效果');

E100=colorseg('euclidean',f,100,m);
subplot(2,2,4),imshow(E100);
title('(d)使用euclidean,T=100分割效果');

M25=colorseg('mahalanobis',f,25,m,C);%使用马氏距离分割
figure,subplot(2,2,1),imshow(M25);
title('(e)使用mahalanobis,T=25分割效果');


M50=colorseg('mahalanobis',f,50,m,C);
subplot(2,2,2),imshow(M50);
title('(f)使用mahalanobis,T=50分割效果');


M75=colorseg('mahalanobis',f,75,m,C);
subplot(2,2,3),imshow(M75);
title('(g)使用mahalanobis,T=75分割效果');


M100=colorseg('mahalanobis',f,100,m,C);
subplot(2,2,4),imshow(M100);
title('(h)使用mahalanobis,T=100分割效果');

代码运行效果如下：

过程分析：

由上图可以看出，用函数roipoly交互式地提取感兴趣的区域，得到的结果图像就是想要的区域，而使用’mahalanobis’选项获得的结果与使用’Euclidean’选项获得的结果都与感兴趣的区域有差异，只能得出T越大，分割的图像越明显的结论，但是目前根据这两幅图，确实分析不到为什么结果图与理想结果图差距这么大的原因。

考虑马氏距离与欧式距离特性：马氏距离考虑到各种特性之间的联系，欧式距离将样品的不同属性（即各指标或各变量量纲）之间的差别等同看待，做出是否存在匹配原因的猜想，换一张图继续实验。

实验总结：

图像选取的向日葵图像，但是这次并没有选择分割图像主要部分向日葵，选择分割绿叶，因为从最上面的小女孩图像的分割，可以看出使用’mahalanobis’选项分割图像中唯一人像小女孩，结果图为空白，猜想是否存在匹配原因，mahalanobis会识别图像的类似部分分割，而小女孩图像中只有一个小女孩，所以它匹配不到图像中的相似部分，这也可以解释为什么建筑物图像使用’mahalanobis’选项会出现图像而不是空白，而建筑物图像中截取了建筑物的一小部分，所以会匹配到建筑物的其他部分显示出来，这也可以解释为什么刚好截取的那部分建筑物片段并没有显示出来（小女孩也没有显示出来）。但是截取的绿叶部分竟然在’mahalanobis’选项图中出现，证明我的猜想存在漏洞，后面学习更多知识后再来解释，也希望有其他猜想的博主一起讨论。

'Euclidean’选项分割图像随着T值越大，分割的范围也越大，会把图像中颜色相近的部分都分割掉，可以观察当T为75,100的时候，几乎把所有的绿叶都分割掉，不管是浅绿色还是深绿色，而颜色接近的黄色到最后都被分割掉，可以解释欧式距离将样品的不同属性（即各指标或各变量量纲）之间的差别等同看待。

但是使用’mahalanobis’选项分割图像具有一定的原则，截取的浅绿色叶子，不管是后来的T=50,75,100，都会选择范围内的浅绿色叶子截取，所以相对而言如果追求分割的准确度使用马氏距离彩色分割算法优势明显。

该原理应该可以不止用在图像分割，图像匹配，人脸识别各种应该也能用到，百度后发现很早就有基于马氏距离的半监督鉴别分析及人脸识别等，慢慢再深入学习吧。