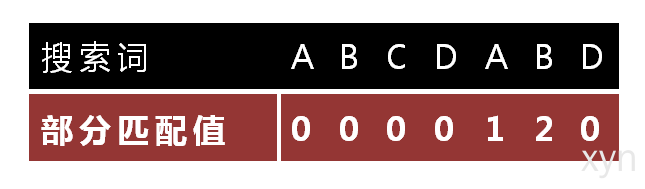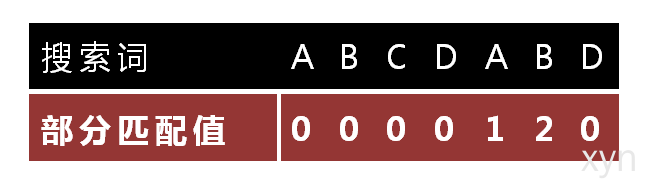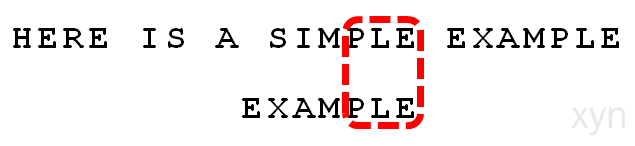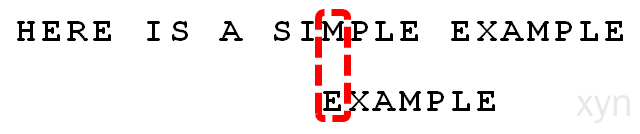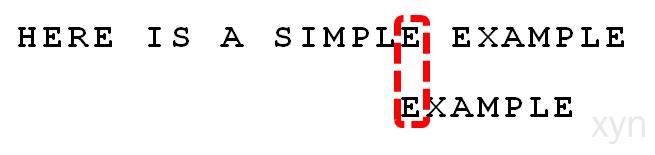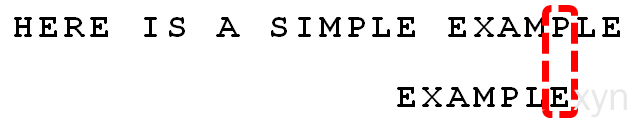面试题: 判断字符串是否在另一个字符串中存在?
面试时发现好多人回答不好, 所以就梳理了一下已知的方法, 此文较长, 需要耐心的看下去。从实现和算法原理两方面解此问题, 其中有用PHP原生方法实现也有一些业界大牛创造的算法。
实现
方法一: 语言特性-内置函数
| 函数 | 描述 | 版本 |
|---|---|---|
| strpos | 查找字符串首次出现的位置 | PHP 4, PHP 5, PHP 7 |
| stripos | 查找字符串首次出现的位置(不区分大小写) | PHP 5, PHP 7 |
| strrpos | 计算指定字符串在目标字符串中最后一次出现的位置 | PHP 4, PHP 5, PHP 7 |
| strripos | 计算指定字符串在目标字符串中最后一次出现的位置(不区分大小写) | PHP 5, PHP 7 |
| mb_strpos | 查找字符串在另一个字符串中首次出现的位置 | PHP 4 >= 4.0.6, PHP 5, PHP 7 |
| strstr | 查找字符串的首次出现 | PHP 4, PHP 5, PHP 7 |
| stristr | strstr() 函数的忽略大小写版本 | PHP 4, PHP 5, PHP 7 |
| substr_count | 计算字串出现的次数 | PHP 4, PHP 5, PHP 7 |
方法二: 语言特性-正则匹配
| 函数 | 描述 | 版本 |
|---|---|---|
| preg_match | 执行匹配正则表达式 | PHP 4, PHP 5, PHP 7 |
| preg_match_all | 执行一个全局正则表达式匹配 | PHP 4, PHP 5, PHP 7 |
方法三: 语言特性-字符串分割
= 2 ? true : false;
}
// strtok 可以么?
// 在分割字符串时,split()与explode()谁快?| 函数 | 描述 | 版本 |
|---|---|---|
| strtok | 标记分割字符串 | PHP 4, PHP 5, PHP 7 |
| explode | 使用一个字符串分割另一个字符串 | PHP 4, PHP 5, PHP 7 |
| split | 用正则表达式将字符串分割到数组中 | PHP 4, PHP 5 |
| mb_split | 使用正则表达式分割多字节字符串 | PHP 4 >= 4.2.0, PHP 5, PHP 7 |
| preg_split | 通过一个正则表达式分隔字符串 | PHP 4, PHP 5, PHP 7 |
方法四: 很暴力的查找
$aLen) {
return -1;
}
$data = [];
$aLastIndex = -1;
$bStartIndex = 0;
for($ai = 0; $ai < $aLen; $ai++) {
$av = $aArr[$ai];
$exists = false;
for($bi = $bStartIndex; $bi < $bLen; $bi++) {
$bv = $bArr[$bi];
if(($aLastIndex == -1 || $ai == ($aLastIndex + 1)) && $av == $bv) {
$exists = true;
break;
}
if ($aLastIndex != -1 && $ai == ($aLastIndex + 1) && $av != $bv) {
break;
}
}
if ($exists) {
$aLastIndex = $ai;
$bStartIndex = $bi + 1;
array_push($data, [
'value' => $av,
'index' => $ai
]);
} else {
$aLastIndex = -1;
$bStartIndex = 0;
$data = [];
}
if ($exists && $bLen == $bStartIndex) {
break;
}
}
if(!empty($data) && count($data) == $bLen) {
$begin = array_shift($data);
return $begin['index'];
} else {
return -1;
}
}方法五: 朴素算法(暴力查找)
方法六: 字符串查找算法-Rabin-Karp算法
#include
#include
using namespace std;
#define BASE 256
#define MODULUS 101
void RabinKarp(char t[], char p[])
{
int t_len = strlen(t);
int p_len = strlen(p);
// 哈希滚动之用
int h = 1;
for (int i = 0; i < p_len - 1; i++)
h = (h * BASE) % MODULUS;
int t_hash = 0;
int p_hash = 0;
for (int i = 0; i < p_len; i++)
{
t_hash = (BASE * t_hash + t[i]) % MODULUS;
p_hash = (BASE * p_hash + p[i]) % MODULUS;
}
int i = 0;
while (i <= t_len - p_len)
{
// 考虑到哈希碰撞的可能性,还需要用 memcmp 再比对一下
if (t_hash == p_hash && memcmp(p, t + i, p_len) == 0)
cout << p << " is found at index " << i << endl;
// 哈希滚动
t_hash = (BASE * (t_hash - t[i] * h) + t[i + p_len]) % MODULUS;
// 防止出现负数
if (t_hash < 0)
t_hash = t_hash + MODULUS;
i++;
}
}
int main()
{
char t[100] = "It is a test, but not just a test";
char p[10] = "test";
RabinKarp(t, p);
return 0;
} 1,
'e' => 2,
'l' => 3,
'o' => 4,
'w' => 5,
'r' => 6,
'd' => 7,
);
for ($i = 0; $i < $len; $i++) {
$hash .= $hash_table[$str{$i}];
}
return (int)$hash;
}
function rabin_karp($text, $pattern)
{
$n = strlen($text);
$m = strlen($pattern);
$text_hash = hash_string(substr($text, 0, $m), $m);
$pattern_hash = hash_string($pattern, $m);
for ($i = 0; $i < $n-$m+1; $i++) {
if ($text_hash == $pattern_hash) {
return $i;
}
$text_hash = hash_string(substr($text, $i, $m), $m);
}
return -1;
}
// 2
echo rabin_karp('hello world', 'ello');方法七: 字符串查找算法-KMP
public class KMP {
public static int KMPSearch(String txt, String pat, int[] next) {
int M = txt.length();
int N = pat.length();
int i = 0;
int j = 0;
while (i < M && j < N) {
if (j == -1 || txt.charAt(i) == pat.charAt(j)) {
i++;
j++;
} else {
j = next[j];
}
}
if (j == N)
return i - j;
else
return -1;
}
public static void getNext(String pat, int[] next) {
int N = pat.length();
next[0] = -1;
int k = -1;
int j = 0;
while (j < N - 1) {
if (k == -1 || pat.charAt(j) == pat.charAt(k)) {
++k;
++j;
next[j] = k;
} else
k = next[k];
}
}
public static void main(String[] args) {
String txt = "BBC ABCDAB CDABABCDABCDABDE";
String pat = "ABCDABD";
int[] next = new int[pat.length()];
getNext(pat, next);
System.out.println(KMPSearch(txt, pat, next));
}
}方法八: 字符串查找算法-Boyer-Moore
public class BoyerMoore {
public static void getRight(String pat, int[] right) {
for (int i = 0; i < 256; i++){
right[i] = -1;
}
for (int i = 0; i < pat.length(); i++) {
right[pat.charAt(i)] = i;
}
}
public static int BoyerMooreSearch(String txt, String pat, int[] right) {
int M = txt.length();
int N = pat.length();
int skip;
for (int i = 0; i <= M - N; i += skip) {
skip = 0;
for (int j = N - 1; j >= 0; j--) {
if (pat.charAt(j) != txt.charAt(i + j)) {
skip = j - right[txt.charAt(i + j)];
if (skip < 1){
skip = 1;
}
break;
}
}
if (skip == 0)
return i;
}
return -1;
}
public static void main(String[] args) {
String txt = "BBC ABCDAB AACDABABCDABCDABDE";
String pat = "ABCDABD";
int[] right = new int[256];
getRight(pat,right);
System.out.println(BoyerMooreSearch(txt, pat, right));
}
}
方法九: 字符串查找算法-Sunday
public class Sunday {
public static int getIndex(String pat, Character c) {
for (int i = pat.length() - 1; i >= 0; i--) {
if (pat.charAt(i) == c)
return i;
}
return -1;
}
public static int SundaySearch(String txt, String pat) {
int M = txt.length();
int N = pat.length();
int i, j;
int skip = -1;
for (i = 0; i <= M - N; i += skip) {
for (j = 0; j < N; j++) {
if (txt.charAt(i + j) != pat.charAt(j)){
if (i == M - N)
break;
skip = N - getIndex(pat, txt.charAt(i + N));
break;
}
}
if (j == N)
return i;
}
return -1;
}
public static void main(String[] args) {
String txt = "BBC ABCDAB AACDABABCDABCDABD";
String pat = "ABCDABD";
System.out.println(SundaySearch(txt, pat));
}
}方法十: 字符串查找算法-BF算法(Brute Force)
#include
#include
#include
int index_bf(char *s,char *t,int pos);
int index_bf_self(char *s,char *t,int index);
int main()
{
char s[]="6he3wor"; //标准BF算法中,s[0]和t[0]存放的为字符串长度。
char t[]="3wor";
int m=index_bf(s,t,2); //标准BF算法
printf("index_bf:%d\n",m);
m=index_bf_self(s,t,2); //修改版BF算法,s和t中,不必再存放字符串长度。
printf("index_bf_self:%d\n",m);
exit(0);
}
/*
字符串S和T中,s[0],t[0]存放必须为字符串长度
例:s[]="7hi baby!" T[]="4baby" index_bf(s,t,1);
pos:在S中要从下标pos处开始查找T
(说明:标准BF算法中,为研究方便,s[0],t[0]中存放的为各自字符串长度。)
*/
int index_bf(char *s,char *t,int pos)
{
int i,j;
if(pos>=1 && pos <=s[0]-'0')
{
i=pos;
j=1;
while(i<=s[0]-'0'&&j<=t[0]-'0')
{
if(s[i]==t[j])
{
i++;
j++;
}
else
{
j=1;
i=i-j+2;
}
if(j>t[0]-'0')
{
return i-t[0]+'0';
}
}
return -1;
}
else
{
return -1;
}
}
/*
修改版,字符串s和t中,不必再包含字符串长度。
例:s[]="hi baby" t[]="baby" index_bf_self(s,t,0);
index:在s中,从几号下标开始查找
*/
int index_bf_self(char *s,char *t,int index)
{
int i=index,j=0;
while(s[i]!='\0')
{
while(*(t+j)!='\0' && *(s+i+j)!='\0')
{
if(*(t+j)!=*(s+i+j))
break;
j++;
}
if(*(t+j)=='\0')
{
return i;
}
i++;
j=0;
}
return -1;
} 方法十一: Aho-Corasick 算法
////////////////////////////////////////////////////
/*
程序说明:多模式串匹配的AC自动机算法
自动机算法可以参考《柔性字符串匹配》里的相应章节,讲的很清楚
*/
#include
#include
const int MAXQ = 500000+10;
const int MAXN = 1000000+10;
const int MAXK = 26; //自动机里字符集的大小
struct TrieNode
{
TrieNode* fail;
TrieNode* next[MAXK];
bool danger; //该节点是否为某模式串的终结点
int cnt; //以该节点为终结点的模式串个数
TrieNode()
{
fail = NULL;
memset(next, NULL, sizeof(next));
danger = false;
cnt = 0;
}
}*que[MAXQ], *root;
//文本字符串
char msg[MAXN];
int N;
void TrieInsert(char *s)
{
int i = 0;
TrieNode *ptr = root;
while(s[i])
{
int idx = s[i]-'a';
if(ptr->next[idx] == NULL)
ptr->next[idx] = new TrieNode();
ptr = ptr->next[idx];
i++;
}
ptr->danger = true;
ptr->cnt++;
}
void Init()
{
int i;
char s[100];
root = new TrieNode();
scanf("%d", &N);
for(i = 0; i < N; i++)
{
scanf("%s", s);
TrieInsert(s);
}
}
void Build_AC_Automation()
{
int rear = 1, front = 0, i;
que[0] = root;
root->fail = NULL;
while(rear != front)
{
TrieNode *cur = que[front++];
for(i = 0; i < 26; i++)
if(cur->next[i] != NULL)
{
if(cur == root)
cur->next[i]->fail = root;
else
{
TrieNode *ptr = cur->fail;
while(ptr != NULL)
{
if(ptr->next[i] != NULL)
{
cur->next[i]->fail = ptr->next[i];
if(ptr->next[i]->danger == true)
cur->next[i]->danger = true;
break;
}
ptr = ptr->fail;
}
if(ptr == NULL) cur->next[i]->fail = root;
}
que[rear++] = cur->next[i];
}
}
}
int AC_Search()
{
int i = 0, ans = 0;
TrieNode *ptr = root;
while(msg[i])
{
int idx = msg[i]-'a';
while(ptr->next[idx] == NULL && ptr != root) ptr = ptr->fail;
ptr = ptr->next[idx];
if(ptr == NULL) ptr = root;
TrieNode *tmp = ptr;
while(tmp != NULL && tmp->cnt != -1)
{
ans += tmp->cnt;
tmp->cnt = -1;
tmp = tmp->fail;
}
i++;
}
return ans;
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
Init();
Build_AC_Automation();
//文本
scanf("%s", msg);
printf("%d\n", AC_Search());
}
return 0;
} 伪方法一: 字符串转数组, 取交集, 判断结果
/*
字符串转数组, 取交集, 判断结果
*/
// demo
echo 'match:', str_match('xasfsdfbk', 'xasfsdfbk') !== false ? 'true' : 'false', ';', PHP_EOL;
echo 'match:', str_match('xasfsdfbk', 'fbk') !== false ? 'true' : 'false', ';', PHP_EOL;
echo 'match:', str_match('xasfsdfbk', 'xs') != false ? 'true' : 'false', ';', PHP_EOL;
echo 'match:', str_match('xasfsdfbk', 'sfs') !== false ? 'true' : 'false', ';', PHP_EOL;
// code
function str_match($a, $b) {
$aArr = str_split($a);
$bArr = str_split($b);
return join('', array_intersect($aArr, $bArr)) == $b;
}
// 集合中的元素具有唯一性, 被匹配的字符串中有相同的字符, 将会去重
// 不能保证交集后的元素顺序连续算法原理
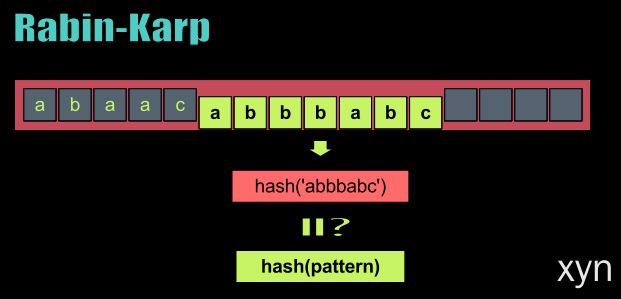
算法一: Rabin-Karp算法(Karp-Rabin)
Rabin-Karp 算法(也可以叫 Karp-Rabin 算法),由 Richard M. Karp 和 Michael O. Rabin 在 1987 年发表,它也是用来解决多模式串匹配问题的。
它的实现方式有点与众不同,首先是计算两个字符串的哈希值,然后通过比较这两个哈希值的大小来判断是否出现匹配。
选择一个合适的哈希函数很重要。假设文本串为t[0, n),模式串为p[0, m),其中 0t[i, j]的哈希值。
当 Hash(t[0, m-1])!=Hash(p[0,m-1]) 时,我们很自然的会把 Hash(t[1, m]) 拿过来继续比较。在这个过程中,若我们重新计算字符串t[1, m]的哈希值,还需要 O(n) 的时间复杂度,不划算。观察到字符串t[0, m-1]与t[1, m]中有 m-1 个字符是重合的,因此我们可以选用滚动哈希函数,那么重新计算的时间复杂度就降为 O(1)。
Rabin-Karp 算法选用的滚动哈希函数主要是利用 Rabin fingerprint 的思想,举个例子,计算字符串t[0, m - 1]的哈希值的公式如下,
Hash(t[0,m-1]) = t[0]*bm-1 + t[1]*bm-2 + ... + t[m-1]*b0其中的 b 是一个常数,在 Rabin-Karp 算法中,我们一般取值为 256,因为一个字符的最大值不超过 255。上面的公式还有一个问题,哈希值如果过大可能会溢出,因此我们还需要对其取模,这个值应该尽可能大,且是质数,这样可以减小哈希碰撞的概率,在这里我们就取 101。
则计算字符串t[1, m]的哈希值公式如下,
Hash(t[1,m]) = ( Hash(t[0,m−1]) − t[0]∗bm−1 ) ∗ b + t[m]∗b0算法二: KMP算法(Knuth Morris Pratt)
许多算法可以完成这个任务,Knuth-Morris-Pratt算法(简称KMP)是最常用的之一。它以三个发明者命名,起头的那个K就是著名科学家Donald Knuth。
这种算法不太容易理解,网上有很多解释,但读起来都很费劲。直到读到Jake Boxer的文章,才真正理解这种算法。下面是阮一峰对KMP算法解释。
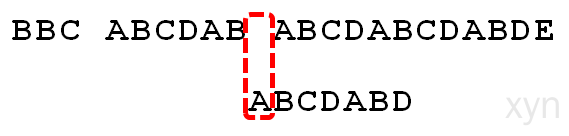
- 首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。
- 因为B与A不匹配,搜索词再往后移。
- 就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
- 接着比较字符串和搜索词的下一个字符,还是相同。
- 直到字符串有一个字符,与搜索词对应的字符不相同为止。
- 这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
- 一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
- 怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
9.已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值- 因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
- 因为空格与A不匹配,继续后移一位。
- 逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
- 逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
- 下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。
"前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
| 概念 | 描述 | 字符串示例 "bread" |
|---|---|---|
| 前缀 | 除了最后一个字符以外,一个字符串的全部头部组合 | b, br, bre, brea |
| 后缀 | 除了第一个字符以外,一个字符串的全部尾部组合 | read, ead, ad, d |
- 部分匹配值实例
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
| 字符串 | 前缀 | 后缀 | 共有元素 | 共有元素长度 |
|---|---|---|---|---|
| A | [] | [] | [] | 0 |
| AB | [A] | [B] | [] | 0 |
| ABC | [A, AB] | [BC, C] | [] | 0 |
| ABCD | [A, AB, ABC] | [BCD, CD, D] | [] | 0 |
| ABCDA | [A, AB, ABC, ABCD] | [BCDA, CDA, DA, A] | [A] | 1 |
| ABCDAB | [A, AB, ABC, ABCD, ABCDA] | [BCDAB, CDAB, DAB, AB, B] | [AB] | 2 |
| ABCDABD | [A, AB, ABC, ABCD, ABCDA, ABCDAB] | [BCDABD, CDABD, DABD, ABD, BD, D] | [] | 0 |
- "部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
算法三: Boyer-Moore算法
KMP算法并不是效率最高的算法,实际采用并不多。各种文本编辑器的"查找"功能(Ctrl+F),大多采用Boyer-Moore算法。
Boyer-Moore算法不仅效率高,而且构思巧妙,容易理解。1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了这种算法。
下面是阮一峰根据Moore教授的例子对Boyer-Moore算法的解释。
- 假定字符串为"HERE IS A SIMPLE EXAMPLE",搜索词为"EXAMPLE"。
- 首先,"字符串"与"搜索词"头部对齐,从尾部开始比较。
这是一个很聪明的想法,因为如果尾部字符不匹配,那么只要一次比较,就可以知道前7个字符(整体上)肯定不是要找的结果。
我们看到,"S"与"E"不匹配。这时,"S"就被称为"坏字符"(bad character),即不匹配的字符。我们还发现,"S"不包含在搜索词"EXAMPLE"之中,这意味着可以把搜索词直接移到"S"的后一位。
- 依然从尾部开始比较,发现"P"与"E"不匹配,所以"P"是"坏字符"。但是,"P"包含在搜索词"EXAMPLE"之中。所以,将搜索词后移两位,两个"P"对齐。
- 我们由此总结出"坏字符规则":
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置如果"坏字符"不包含在搜索词之中,则上一次出现位置为 -1。
以"P"为例,它作为"坏字符",出现在搜索词的第6位(从0开始编号),在搜索词中的上一次出现位置为4,所以后移 6 - 4 = 2位。再以前面第二步的"S"为例,它出现在第6位,上一次出现位置是 -1(即未出现),则整个搜索词后移 6 - (-1) = 7位。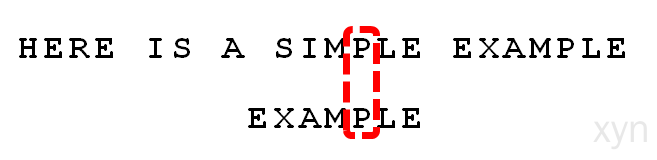
- 依然从尾部开始比较,"E"与"E"匹配。
- 比较前面一位,"LE"与"LE"匹配。
- 比较前面一位,"PLE"与"PLE"匹配。
- 比较前面一位,"MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀"(good suffix),即所有尾部匹配的字符串。注意,"MPLE"、"PLE"、"LE"、"E"都是好后缀。
- 比较前一位,发现"I"与"A"不匹配。所以,"I"是"坏字符"。
- 根据"坏字符规则",此时搜索词应该后移 2 - (-1)= 3 位。问题是,此时有没有更好的移法?
- 我们知道,此时存在"好后缀"。所以,可以采用"好后缀规则":
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置举例来说,如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
再举一个例子,如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。
这个规则有三个注意点:
- (1)"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。
- (2)如果"好后缀"在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。
- (3)如果"好后缀"有多个,则除了最长的那个"好后缀",其他"好后缀"的上一次出现位置必须在头部。比如,假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B",请问这时"好后缀"的上一次出现位置是什么?回答是,此时采用的好后缀是"B",它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个"好后缀"只出现一次,则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB",即虚拟加入最前面的"DA"。
回到上文的这个例子。此时,所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。
12.可以看到,"坏字符规则"只能移3位,"好后缀规则"可以移6位。所以,Boyer-Moore算法的基本思想是,每次后移这两个规则之中的较大值。
更巧妙的是,这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
- 继续从尾部开始比较,"P"与"E"不匹配,因此"P"是"坏字符"。根据"坏字符规则",后移 6 - 4 = 2位。
- 从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据"好后缀规则",后移 6 - 0 = 6位,即头部的"E"移到尾部的"E"的位置。
算法四: Sunday算法
Sunday算法由Daniel M.Sunday在1990年提出,它的思想跟BM算法很相似:1
只不过Sunday算法是从前往后匹配,在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。
如果该字符没有在模式串中出现则直接跳过,即移动位数 = 模式串长度 + 1;
否则,其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。
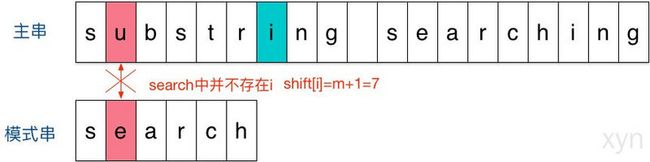
下面举个例子说明下Sunday算法。假定现在要在主串”substring searching”中查找模式串”search”。
结果发现在第2个字符处发现不匹配,不匹配时关注主串中参加匹配的最末位字符的下一位字符,即标粗的字符 i,因为模式串search中并不存在i,所以模式串直接跳过一大片,向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7,从 i 之后的那个字符(即字符n)开始下一步的匹配,如下图: 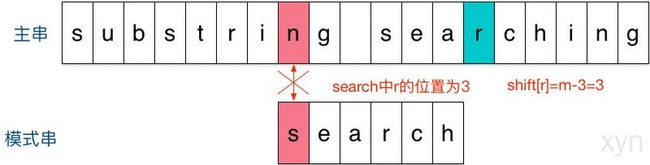
结果第一个字符就不匹配,再看主串中参加匹配的最末位字符的下一位字符,是’r’,它出现在模式串中的倒数第3位,于是把模式串向右移动3位(m - 3 = 6 - 3 = r 到模式串末尾的距离 + 1 = 2 + 1 =3),使两个’r’对齐,如下: 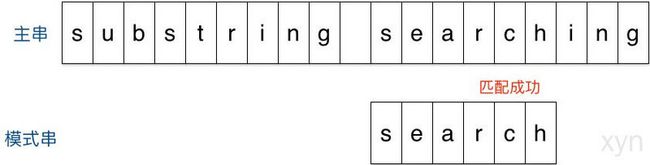
匹配成功。
回顾整个过程,我们只移动了两次模式串就找到了匹配位置,缘于Sunday算法每一步的移动量都比较大,效率很高。
算法五: BF算法(Brute Force)
BF算法核心思想是:首先S[1]和T[1]比较,若相等,则再比较S[2]和T[2],一直到T[M]为止;若S[1]和T[1]不等,则T向右移动一个字符的位置,再依次进行比较。如果存在k,1≤k≤N,且S[k+1…k+M]=T[1…M],则匹配成功;否则失败。该算法最坏情况下要进行M(N-M+1)次比较,时间复杂度为O(MN)。下面结合图片,解释一下:
S代表源字符串,T代表我们要查找的字符串。BF算法可以表述如下:依次遍历字符串S,看是否字符串S中含有字符串T。
因此,我们依次比较S[0] 和T[0]、S[1] 和T[1]、S[2] 和T[2]……S[n]和T[n] ,从图中我们可知,S[0]-S[7]和T[0]-T[7]依次相等。当匹配到S[8]和T[8]时,两个字符不等。根据定义,此时S和T都要回溯,T向右移动一个字符的位置,即S回溯到S[1]的位置,T回溯到T[0]的位置,再重新开始比较。此时,S[1]和T[0]、S[2]和T[1]……如果再次发现不匹配字符,则再次回溯,即S回溯到S[2]的位置,T回到T[0]的位置。循环往复,直到到达S或者T字符串的结尾。如果是到达S串的结尾,则表示匹配失败,如果是到达T串的结尾,则表示匹配成功。
BF算法优点:思想简单,直接,无需对字符串S和T进行预处理。缺点:每次字符不匹配时,都要回溯到开始位置,时间开销大。
算法六: Aho-Corasick算法
Aho-Corasick算法又叫AC自动机算法,是一种多模式匹配算法。Aho-Corasick算法可以在目标串查找多个模式串,出现次数以及出现的位置。
Aho-Corasick算法主要是应用有限自动机的状态转移来模拟字符的比较,下面对有限状态机做几点说明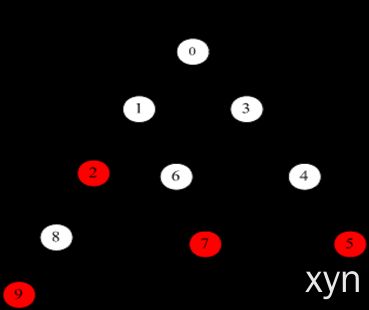
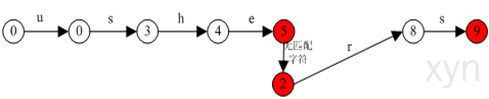
上图是由多模式串{he,she,his,hers}构成的一个有限状态机:
1.该状态当字符匹配是按实线标注的状态进行转换,当所有实线路径都不满足(即下一个字符都不匹配时)按虚线状态进行转换。
当转移到红色结点时表示已经匹配并且获得模式串
Aho-Corasick算法步骤
Aho-Corasick算法和前面的算法一样都要对模式串进行预处理,预处理主要包括字典树Tire的构造,构建状态转移表(goto),失效函数(failure function),输出表(Output)。
Aho-Corasick算法包括以下3个步骤
- 构建字典树Tire
- 构建状态转移表,失效函数(failure function),输出表(Output)
- 搜索路径(进行匹配)
下面3个步骤分别进行介绍
- 构建字典树Tire
Tire是哈希树的变种,Tire树的边是模式串的字符,结点就是Tire的状态表,下图是多模式串{he,she,his,hers}的Tire树结构: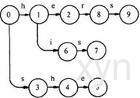
- 构建goto函数、failure function和Output函数
- goto函数(状态转移函数):goto(pre,v)=next,完成这样的任务:在当前状态pre,输入字符v,得到下一个状态next,如果没有下个状态则next=failure。
- failure function:失效函数是处理当前状态是failure时的处理。
- output函数:当完成匹配是根据状态输出匹配的模式串。
下面是多模式串{he,she,his,hers}的goto函数,failure函数,output函数
| 函数 | 结构图 |
|---|---|
| goto函数 | 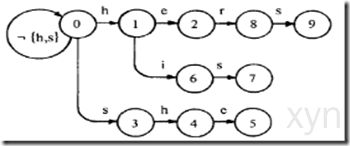 |
| failure函数 |  |
| output函数 |  |
特点
一般而言,好的字符串匹配算法要有以下特点:
速度快
这是评价一个字符匹配算法最重要的标准。通常要求字符匹配能以线性速度执行。
有几种时间复杂性的评价指标
| 序号 | 指标 | 描述 |
|---|---|---|
| 1) | 预处理时间的复杂性 | 有些算法在进行字符串匹配前需要对模式特征进行预处理 |
| 2) | 匹配阶段的时间复杂性 | 字符串匹配过程中执行查找操作的时间复杂性,它通常和文本长度及模式长度相关 |
| 3) | 最坏情况下的时间复杂性 | 对一个text进行字符模式匹配时,设法降低各算法的最坏情况下的时间复杂性是目前的研究热点之一 |
| 4) | 最好情况下的时间复杂性 | 对一个text进行字符模式匹配时的最好的可能性。 |
内存占用少
执行预处理和模式匹配不仅需要CPU资源还需要内存资源,尽管目前内存的容量较以前大得多,但为了提高速度,人们常利用特殊硬件。通常,特殊硬件中内存访问速度很快但容量偏小,这时,占用资源少的算法将更具优势。
参考
- 算法之字符串模式匹配
- 彻底搞定KMP字符串匹配算法
- 浅谈字符串匹配算法—BF 算法及 KMP 算法
- 几种常见的字符串匹配算法
- 字符串查找算法总结(暴力匹配、KMP 算法、Boyer-Moore 算法和 Sunday 算法)
- 字符串匹配算法
- 字符串匹配的KMP算法
- 字符串匹配的Boyer-Moore算法
- KMP算法心得
- 从头到尾彻底理解KMP