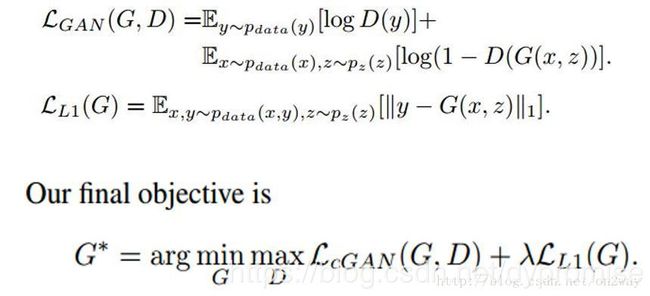由生成模型到domain迁移：GAN、CGAN、StarGAN、CycleGAN、AsymmetricCycleGAN

最近看一篇CVPR2018文章PairedCycleGAN: Asymmetric Style Transfer for Applying and Removing Makeup有感。总结一下GAN做domian transfer的思路脉络。

Base knowledge

GAN

2018/12/14更新: GAN loss的分拆理解

The point is:

1. Loss descent principle for both G and D
2. When update G， we have fixed the D, the vice versa

Generative Adversarial Nets (GAN) :

GAN是一种训练生成模型的方法，包括两个互相对抗的模型：一个生成模型G用于拟合样本数据分布和一个判别模型D用于估计输入样本是来自于真实的训练数据还是生成模型G。

生成器通过映射函数把噪声映射到数据空间，而判别器的输出是一个标量，表示数据来自真实训练数据而非G的生成数据的概率。

G和D非线性的映射函数，例如多层感知机等。

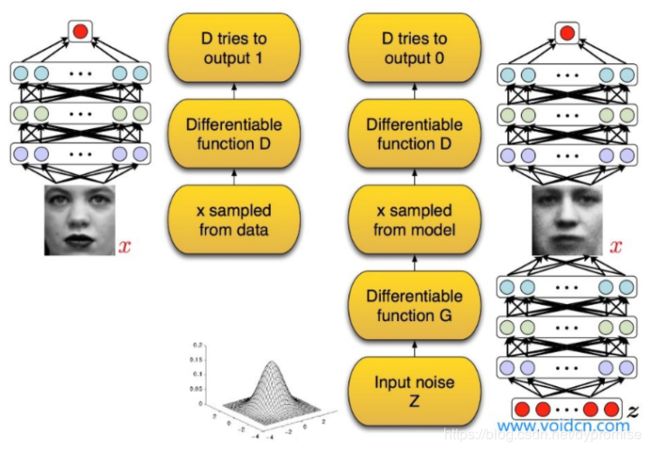
上图左边表示对于判别模型D，如果输入为真实的训练数据，那么模型最终的输出应该接近于1。上图右侧表示如果判别模型的输入为由G生成的样本，那么D的最终输出应该期望接近于0。

GAN模型没有损失函数，优化过程是一个“二元极小极大博弈(minimax two-player game)”问题，下面是模型的价值函数：

$$\underset{G}{\min }\underset{D}{\max }V(D,G)=E_{x\sim p_{data}(x)}[logD(x)]+E_{z\sim p_z(z)}[log(1-D(G(z)))]$$

训练模型D要最大概率地分对真实样本（最大化log(D(x))，而生成模型G要最小化log(1-D(G(z)))，即最大化D的损失。G和D同时训练，但是训练中要固定一方，更新另一方的参数，交替迭代，使对方的错误最大化。最终，G能估计出真实样本的分布。在查资料时看过一个比喻：GAN的训练过程可以被比作警察抓小偷的过程—生成模型G是小偷，判别模型D是警察。也就是说，对于小偷G要尽可能提高自己的手段，来骗过警察D，而对于警察D来说，要提高自己的能力来识别出小偷G。所以，GAN框架下的学习过程就变成了一种生成模型G和判别模型D之间的竞争关系。最终判别模型的准确率等于50%，整个模型状态达到纳什均衡。

但是由于GAN这种不需要预先建模的方法太过自由，如果对于较大图片，较多像素的情形，这种基于GAN的方法就太不可控了。

Conditional GAN

为了解决上述问题，自然就想到给GAN模型加入一些条件约束，也就有了本文的工作Conditional Generative Adversarial Nets(CGAN)。在生成模型G和判别模型D中同时加入条件约束y来引导数据的生成过程。条件可以是任何补充的信息，如类标签，其它模态的数据等，这样使得GAN能够更好地被应用于跨模态问题，例如图像自动标注。

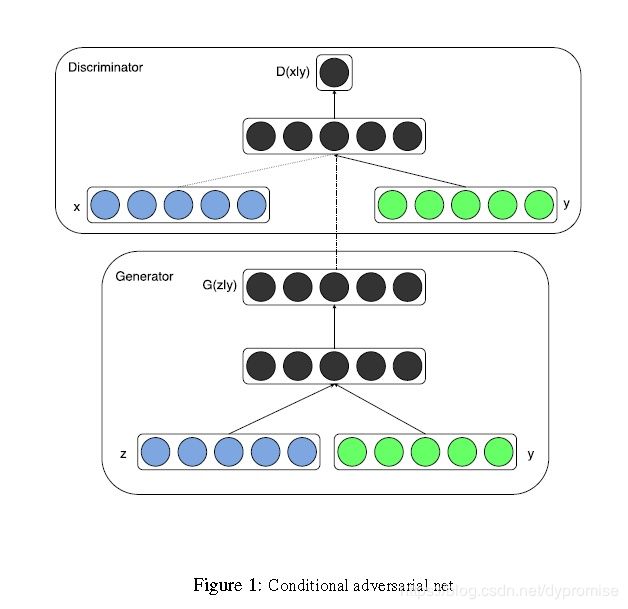
上图所示是CGAN的结构。
把噪声z和条件y作为输入同时送进生成器，生成跨域向量，再通过非线性函数映射到数据空间。
把数据x和条件y作为输入同时送进判别器，生成跨域向量，并进一步判断x是真实训练数据的概率。

$$\underset{G}{\min }\underset{D}{\max }V(D,G)=E_{x\sim p_{data}(x)}[logD(x|y)]+E_{z\sim p_z(z)}[log(1-D(G(z|y)))]$$

在MNIST上以数字类别标签为约束条件，最终根据类别标签信息，生成对应的数字。
生成模型的输入是100维服从均匀分布的噪声向量，条件y是类别标签的one hot编码。噪声z和标签y分别映射到隐层（200和1000个unit），在被第二次映射前，连接了所有120个unit。最终用一个sigmoid层输出784维(28*28)的单通道图像。

判别模型把输入图像x映射到一个有240个unit和5 pieces的maxout layer，把y映射到有50个unit和5pieces的maxout layer。同时，把所有隐层连在一起成为sigmoid层之前的有240个unit和4pieces的maxout layer。最终的输出是该样本x来自训练集的概率。
该节分享两篇使用GAN的方法来进行图像转换方面的文章，分别是pix2pix GAN 和 Cycle GAN，两篇文章基本上是相同的作者发表的递进式系列，文章不是最新，但也不算旧，出来半年多点，算是比较早的使用GAN的方法进行图像转换的文章吧，该部分将详细解读其实现过程。

Applacation

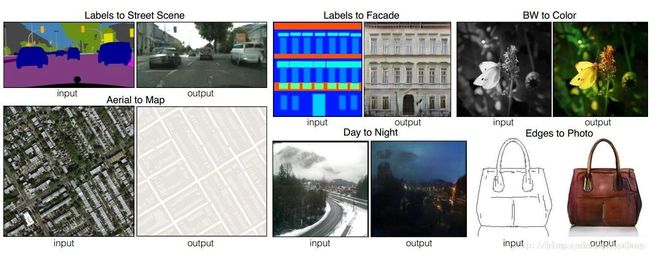
图像转换或者图像的风格转换，顾名思义，是指把一副图像A按照另一幅 图像B的模式/风格进行转换的一个操作，例如 “白天->黑夜”，“晴天->雨天”等等；

Papers

在深度学习的方法广泛应用以后，使用深度学习方法比较早做这件事的就是使用CNN框架来做的，也就是2016cvpr的一篇文章“Image style transfer using convolutional neural networks”基于深度卷积神经网络的方法。当时出来的时候也比较火，也有一些方法在此类方法上的改进。

随着生成对抗网络（GAN）这种在图像生成上具有天生强大能力的网络结构的出现，使用GAN方法做图像生成又成为了一个比较流行的方法。列举几个截止到目前使用GAN为基础的方法：

• pix2pix GAN (1611)
• CycleGAN (1703)
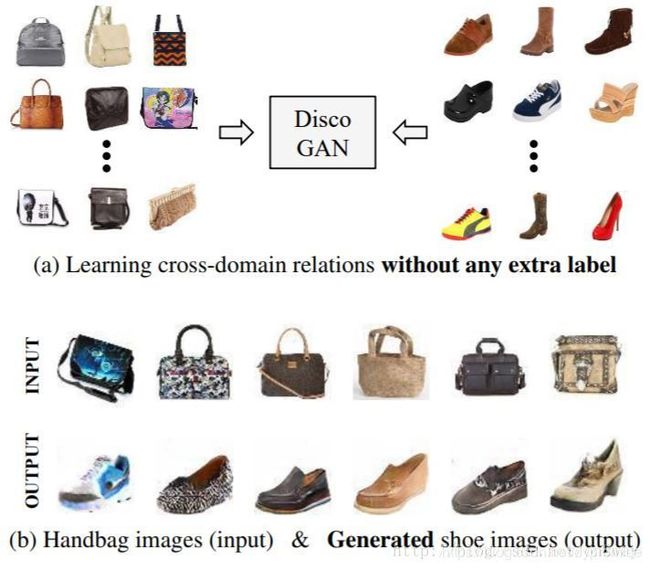
• DiscoGAN (1703)
• PAN（ Perceptual Adversarial Networks）感知GAN (1706)
• StarGAN (1711)

这些方法的最终效果上可能都是为了进行图像转换，实现的形式不同而已。包括最近出来的StarGAN。

先简单看下各类方法一个效果:

• Gatyes et.al.
  祖师爷风格迁移的开山之作
  

• pix2pix GAN
  

• CycleGAN
  

• DiscoGAN

• PAN

• StarGAN

Details

pix2pix GAN

先来看看第一篇文章pix2pix GAN，文章全名“Image-to-Image Translation with Conditional Adversarial Networks”

文章的框架如图所示：

来看一下这个框架，整个框架依托cGAN的思想，判别网络的输入是一个两张图组成给的数据结构，可以认为是图+label，可能有人会奇怪，这里的label为什么是一张图，这怎么是cGAN呢，我们前面说过，条件GAN接受的条件并不一定都是低维度的数值，也可以是广义的label，这里就可以认为右边的那个白色的图就是label，如果我们常见的GAN的判别器的输入是一个rgb三通道的图像的话，这里就好比输入的是一个6通道的两个图叠加的图。那么为什么要这么做呢？主要的原因应该还是为了满足生产器，其次是为了使得网络可以有效的训练。

可以看一下上述的判别器部分，此时我们白色的图像充当着噪声的功能，也就是可以把白色图像经过生成器变成黑色的图，同时黑色的图和白色的图叠加作为假样本来训练。这样我们可以发现，对于这一次的真假样本，因为白色的图（好比是label）是一样的，要想使得判别器无法判别真假，那么生成的黑色的图必须尽可能的与真样本的黑色的图像相似才满足条件吧，这也是为什么要把黑白两者叠加在一起作为样本输入的原因。

试想一下，假如只把黑色的当做真假判断条件而没有白色的，那么当把白色A图像送入生成器后，可能生成了黑色B图像，这个时候，黑色A与黑色B对于判别器来说都是真样本，所以判别器很容易没有误差了而生成器也是错的，达不到把白A生成白B的目的。

基于此可以看到这篇文章使用cGAN来实现图像转换的合理性，那么整个的目标函数可以表示如下：

注意的是目标函数包含两项，第一项就是一个一般条件GAN的常规优化函数，至于这个式子怎么理解，为什么要这么写依然可以参考上述的那篇文章。这里重点看一下第二项的一个loss，这可以理解为一个重建误差项，也就是上面白色通过生成器生成的图像（G(x,z)）与原始的黑色图像y之间的误差。(这里的黑白其实可以互换生成)

这个优化目标就是这样，这里的最终目的就是为了得到一个比较好的G，可以将白色转换为黑色，有了这个G也就达到了图像转换的目的了。

G的构造

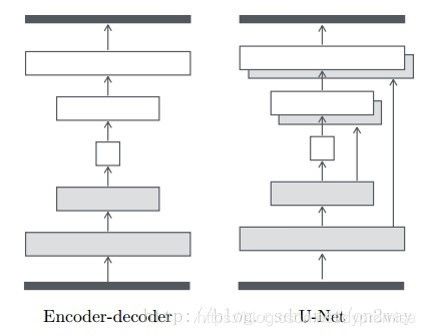
下面来看一下这个G是如何构造的，文章中展示了两种图像生成图像的典型结构，一个是自编码结构，一个是改进的U-Net结构：

很显然，从结构上也知道第二种结构要好，实验也会对比。

图像的patch实验

这篇文章中另一个小的结构点是实验了PatchGAN的方式，也就是对于生成器或者判别器，不是以整个图像整个图像的当做输入，而是以小的patch来进行的。把一副图像划分为N*N个patch后，对于每一块进行上述的那个操作。可以发现当N=1的时候，相当于逐像素进行了，当N=256（图像大小为256的话），就是一幅图像一幅图像的操作。当然文章的实验发现当N=70的时候，效果最好。

其实当N是某一个固定块的一个最大的好处是，可以由小的图像生成大的图像，因为反正你都是对块进行操作的。比如你的原始图像都是256256的，每7070一个块进行的。训练的模型，假如有一个1000*1000的图像需要转换，是不是也可以转换，只需要把1000转成多个70的块，每个块单独转换即可。

文章的实验

文章列举了encoder-decoder与U-Net的不同导致的生成结果的不同的实验。同时也列举了不同的loss导致的结果的不同，可以参考原文。

看几个最终的生成结果的实验：

CycleGAN

domain transfer 神作
论文：Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks17

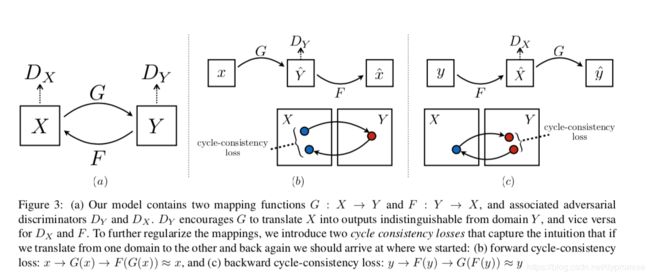
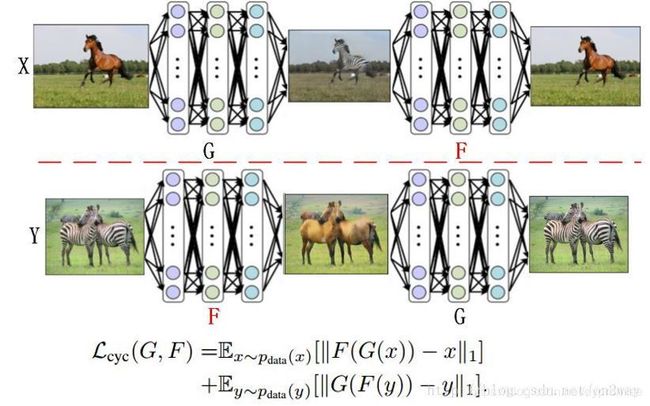
作者提出了一种unpaired的无监督训练方法实现domain transfer。核心就是GAN Adversarial Loss + Consistency Loss。主要是后者实现解放unpaired 训练集的限制：
1）Adversarial loss
$$L_{GAN}(G,D_y,X,Y)=E_{P_{data}(y)}[log{D}_Y(y)]+E_{P_{data}(x)}[log(1-D_Y(G(x)))]$$
2）Cycle Consistency Loss
$$L_{cyc}(G,F)=E_{P_{data}(x)}[||F(G(x))-x|{|}_1]+E_{P_{data}(y)}[log(||G(F(y))-y|{|}_1)]$$

Full Objective:

$$L(G,F,D_X,D_Y)=L_{GAN}(G,D_Y,X,Y)+L_{GAN}(F,D_X,Y,X)+\lambda L_{cyc}(G,F)$$
即求解下面的问题：
$$G^{\ast },F^{\ast }=argmi{n}_{G,F}ma{x}_{D_X,D_Y}L(G,F,D_X,D_Y)$$

理解

首先来想想这篇文章的出发点，这篇文章和上面那篇基本上是一组作者，上面那篇我们已经看到，数据集的一个非常重要的要求就是你的图像必须是成对的，这一点其实是非常苛刻的，现实中很难找到，就好比同一个场景下的白天和黑夜的两幅图，很难找到这样一个大的数据集里面包含完全相同的同一个场景下的白天与黑夜图。那么这篇文章就是为了解决这样一个问题，就是训练集不在需要同一组完全配对的图，只需要两个模式不同的图即可，如下：

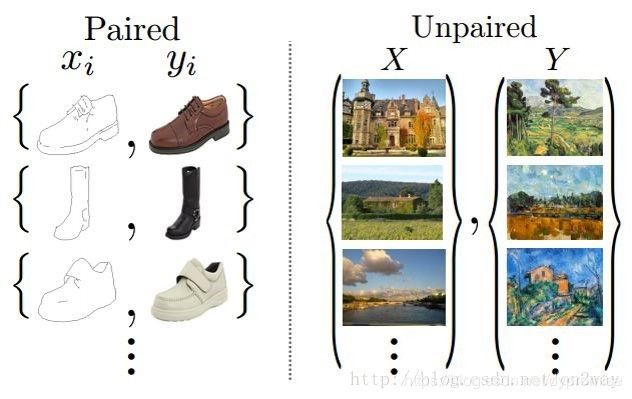
下面来详细探讨下这三类loss，首先是前两个一般情况下的GAN的loss。这里把这两个简化一下如下：

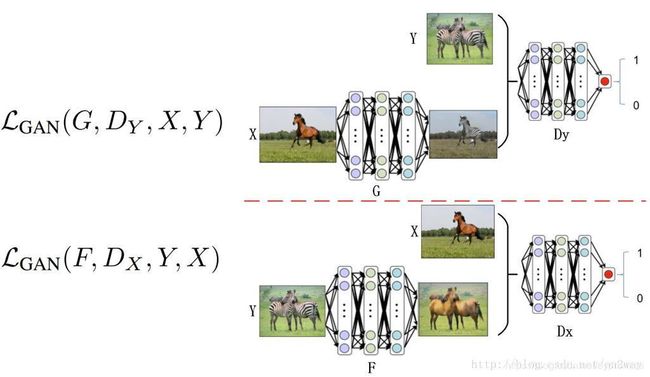
这样应该好理解了，首先是第一类GAN的loss，这里认为Y是真的样本集，而把X作为生成样本集的输入，这样就会产生一类Y模式下的X了，通过Dy来判断真的Y和X生成的假的Y来实现训练的目的。同理把X和Y换个位置就变成了上图下面的情况了。可以说这一过程是非常的巧妙，巧妙在于X与Y都是真样本集，同时又可以实现生成的假样本集，并且并不要求X与Y是同一个物体，只要他们的潜在模式一样即可。

接下来是第三类重建误差loss了，依然用一个图表示下：

这里可以看到，存在着两种重建误差了吧，首先是X的，X经过G可以变成假Y，假Y进F又可以还原会假X，我们的目的就是让真X与假X足够相似，公式表示就是这种重建误差了。这是对于X是这样，同理对于Y也是如此。
看到这里，同样一声惊叹这种设计方法的巧妙。这就是整个loss的构成，基于此，网络可以得到很好的训练了。最终也可以训练得到想要的G，F，Dx,Dy。而G，F才是最好可以用来作为图像转换使用的。

来看几个最终的实验结果吧：

Star-GAN

要引入多domain，必须引入指向domain的监督。于是作者在判别网络中引入一个对domain分类的分类器。

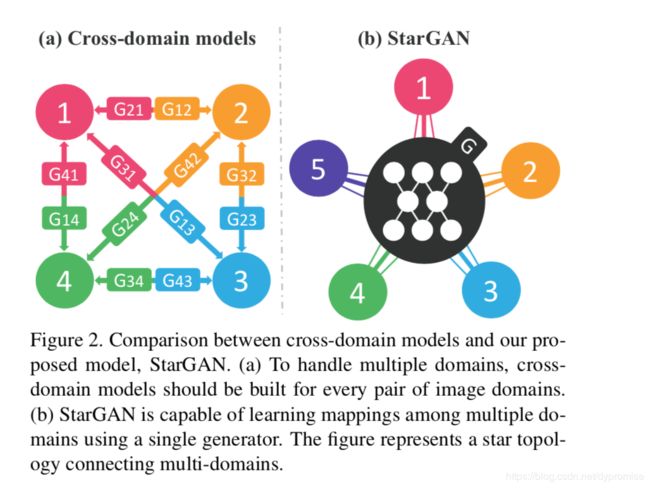
生成网络采用cycleGAN形式。本文提出的网络结构：

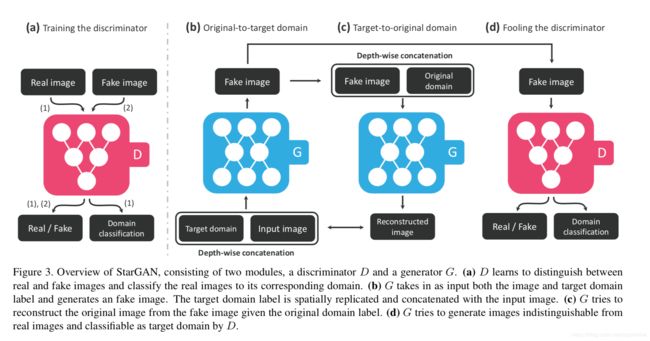
作者将loss分成三部分：
$c$ 代表target domian，$c^{{}^{\prime }}$代表original domain
1）Adversarial loss
$$L_{adv}=E_x[log{D}_{src}(x)]+E_{x,c}[log(1-D_{src}(G(x,c)))]$$
2）Domain classification loss
$$L_{cls}=E_{x,c^{{}^{\prime }}}[-log{D}_{cls}(c^{{}^{\prime }}|x)]+E_{x,c}[-log{D}_{cls}(c|G(x,c))]$$
3）Reconstruction loss
$$L_{rec}=E_{x,c,c^{{}^{\prime }}}[||x-G(G(x,c),c^{{}^{\prime }})|{|}_1$$

效果

但是做实验发现，会有一些鬼脸生成。这个可以尝试PGGAN的方法。

Asymmetric CycleGAN

妆容迁移的一篇文章
CVPR_2018: PairedCycleGAN: Asymmetric Style Transfer for Applying and Removing Makeup
主要结构继承CycleGAN，加了一个知道general domain transfer 的一个 Discriminator。

作者提到，CycleGAN也可以胜任makeup（妆容）迁移的任务，但是生成出来的太过于genreal：
“CycleGAN could in principle learn to apply a general make-you-look-good makeup to a no-makeup face, but it would not replicate a specific example makeup style.” “A second challenge, specific to our makeup problem, is that people are highly sensitive to visual artifacts in rendered faces”

人们对于妆容迁移苛刻、细致的追求导致一些传统的color transfer、style transfer的方法产生的 artifacts (like painting style) 不能容忍。所以，善于脑补（高度feature抽象与生成）的GAN会起到一些帮助作用。但是，某些时候我们做妆容迁移或者人脸属性编辑的时候，我们只想更改某一个部位的apperence，而不改变其他的部位。一般的GAN会将不该改变的部分迁移到source图片上，这并不是理想的结果。

CycleGAN可以解决这个问题。作为一个强化版双向conditional GAN，它拥有前向生成网络G与反向生成网络F，相应的，拥有监督两个domain的Discriminator Dx与Dy。Dx与Dy起到至关重要的作用，Dx区分 $x$ 与 $x^{{}^{\prime }}$, 而Dy区分 $y$ 与 $y^{{}^{\prime }}$。这驱使两个Generator向正确的domain生成图片。

但是问题来了，在相对精细的妆容迁移任务上，GAN的diversity的弊端显的明显。意思是如何让CycleGAN适应任意风格的makeup输入、并且生成的图片不要有artifacts？从StarGAN的思路受到启发，可以设计一个多分类器Discriminator，来指导Gernerator生成多种风格的makeup。但是这样只能是有限种类的makeup。如何可以做到arbitrary makeup输入都可以迁移？本文提出用一个“*an auxiliary discriminator DS, which decides whether a given pair of faces wear the same makeup.”*这样的化巧妙的将范化任意种类的任务转换成判断一pair是否是一样的style这样的问题。甩锅给判别器，只要你train data里面有足够多的style 类型。

效果：

未完待续。