【DL】卷积神经网络(CNN)的介绍与优化
1 CNN简介
是一种以卷积计算为核心的前馈运算神经网络模型,区别于低隐层全连接神经网络模拟轴突树突神经节点,卷积网络类似大脑识别物体的感受野,对特征进行从低维到高维的逐层抽象提取,学习到从边缘、方向、纹理低层特征到高层语义(物体、句子)的特征。
2 网络结构
CNN快速发展,得益于LeNet-5、Alexnet(8层)、ZFNet、VGGNet(19层)、GoogleNet(24层)、ResNet等不同结构的设计出现。
主要设计思路:
- 卷积>激活>池化>卷积>激活>池化>…全连接
2.1 卷积层(convolution layer)
卷积计算:卷积核在图像上按照步长移动,卷积核覆盖的区域内的每个通道图像数据和卷积核对应位置数值相乘求和。参考博客:yjl9122 博客2
卷积的作用就是通过卷积核(深度一般和输入图像相同)作用于图像局部区域获得图像的局部信息,增强提取特征(就是核里的数值和图像数值乘积求和作为输出),类似图像处理中的滤波器,输出的新图像称为feature map特征图。
上图就是两个卷积核,w1和w2,每个卷积核的深度(通道)为4,下一层输出就是两层。
超参数:
-
卷积核(卷积参数,convolution kernel或convolution filter)是一个矩阵,覆盖在图像上边移动边计算。深度不定。
-
卷积步长(stride):核在输入图像上的移动距离。
权重(weight):需要学习的部分, 就是学习到的核参数
权值共享(weight sharing):卷积核在移动过程中是不变的
偏置项(bias term):运算偏置,卷积核求积求和后加个常数,增加非线性。
- 偏置项或者学习率设置为0固定这一层的偏置或者权重。
卷积核作用:
整体边缘滤波器(Ke)、横向边缘滤波器(Kh)、纵向边缘滤波器(Kv)不同核值可以达到提取图像像素显著差异区域,消除差异小的区域,达到检测整体、纵向、横向边缘信息。Kh,Kv 一般也称为sobel滤波器。
2.2 池化(pooling或汇合)
池化操作类似特征的下采样(down-sampling),模仿人对视觉特征的降维抽象,池化操作的输入就是卷积输出的feature map,
提取高级特征。
就是减低卷积输出的特征向量,对池化核区域内的数据有目的选择。
- 特征不变性:更关注是否存在而非具体值。
- 特征降维:维度约简,抽取广泛的特征,减小下层输入,降低计算量。
- 一定程度防止过拟合。
操作运算类似卷积过程,只是不需要学习参数。只需要指明池化类型、池化核大小、池化步长这些超参数就可以,也决定了输出数据的大小维度。
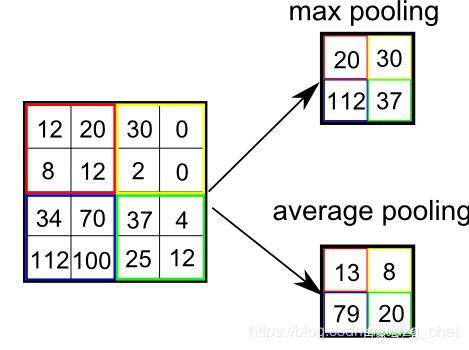
- 均值池化(average-pooling):池化核盖上去,取这个区域的平均值
- 最大值池化(max-pooling):核区域内的最大值
- 随机池化(stochastic-pooling):全局上类似平局,局部类似最大
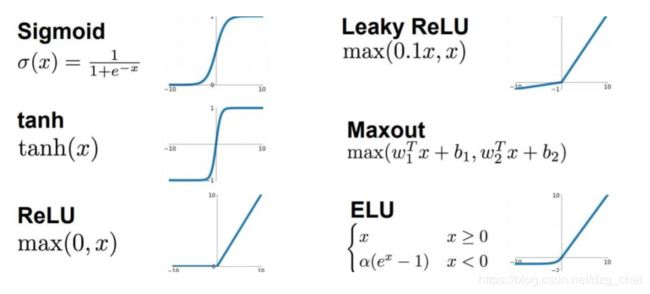
2.3 激活函数(activation function)
模拟生物学中神经元的特性,输入信号到达一个阈值之后才会产生兴奋向下传递,又称非线性映射层(no=linearlity-mapping),增加网络表达非线性的能力。
在网络里对(权重 * 节点参数 * + 偏差 )的运算结果进行激活处理。抛掉一部分达不到阈值的输出。
sigmod函数(logistic):
-
输入无论多大多小输出都会被压缩到【0,1】之间。
-
由它的梯度(导数)函数图像知道,是一个尖峰型,尖峰两边很远的变量导数为0.在误差反向传播时导数处于这部分的误差很难传到钱层,导致参数无法更新,网络无法训练,引发饱和效应(staturation effect)。
ReLU函数(最常用):
- x >= 0,函数梯度为1,反之为0.消除了梯度饱和。
- 有助于随机梯度下降法收敛,收敛速度较logistics快6倍左右。
2.4 全连接层
准确说是Flatten层,将卷积层和池化层操作运算得到的抽象特征映射为一个高维向量(一维),然后用这个向量通过全连接层和分类输出拟合理想的函数,实现学习特征最后目标。方便计算概率和分类预测的输出。
3 经典模型示例(LeNet-5)
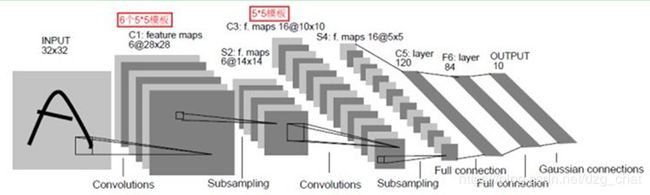
这里要注意的是:随着向后运算的过程,每个卷积核的深度是变化的,如第三层feature_map是6 * 14 * 14,就是每单个卷积核深度为6,进行卷积运算求和加偏置等之后输出为1层feature_map,所以理论上是要有 16个(5 * 5 * 6)的卷积核。实际因为不是全连接,所以不需要那么多卷积核,可以看下文。
3.1 C1卷积
这里一个卷积核可以理解为深度为6,就是一个卷积核包含六个同样尺寸的卷积模板,因为输入是单层的,所以只进行了一次和卷积核的运算。
- 输入尺寸:32*32
- 卷积核大小:5*5
- 卷积核深度(一个卷积核包含的卷积模板数):6
- 输出特征图(神经元节点数量):2828 * 6(步长为1时,5 * 5大小卷积核在32 * 32图像上走完输出图的尺寸是 32-5+1=28)
- 可训练参数:(5*5+1) * 6 (每一个核都需要训练参数和偏置,和池化有区别)
- 网络连接数量:(5 * 5+1)* 6 * 28 * 28
3.2 S2下采样(池化)
这里运算更看重卷积模板运算后的权和偏置,不在意卷积的时候每个模板不同位置的参数。
- 输入特征图:28 * 28 *6
- 采样核:2 * 2 (步长为2)
- 采样核深度:6 (和卷积输出特征深度相同)
- 输出池化特征图:14 * 14 * 6
- 网络连接数量:(2 * 2 + 1)* 6 *14 *14
- 可训练参数:这一步的参数不是训练核里的数值,而是求完和的权(激活),再加上一个偏置,所以训练参数数量:2 * 6
3.3 C3卷积
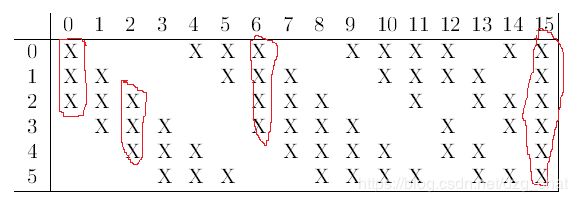
C3里卷积核与S2的特征图是部分连接的,每个卷积核可以看做由不同数量的卷积模板组成的,如下图,前面6次是3个模板作为一个卷积核,中间9个是5个模板作为一次卷积核,最后一次是与S2全连接,6个模板作为一个卷积核。
-
输入:S2 输出的6个池化特征图的组合,即与S2部分连接
-
卷积核大小:5 * 5 (步长 1)
-
卷积核种类:16 (决定输出特征也是16层)
-
输出2次卷积运算后的特征:10 * 10 (14-5+1) 对S2 输出的池化特征图进行组合,(6 + 9 +1)共16层输出。
训练参数(以6+9+1=16为例):
-
16层的C3输出特征图的前6种,是以S2里3个子特征图作为输入运算出来的。一个卷积核是含3个卷积模板。
- 一个卷积核的参数:3 * 5 * 5,再加一个偏置项。6层总参数:6 * (3 * 5 * 5 + 1)
-
C3输出的中间9个特征图,是以S2里的4个特征子图为输入运算出来的,一个卷积核包含4个卷积模板。
- 一个卷积核参数:4 * 5 * 5,加上一个偏置项。9层总参数:9 * (4 * 5 * 5 + 1)
-
C3输出的最后1个特征图,以S2里的全部作为输入,一个卷积核包含6个卷积模板。
- 一个卷积核参数:6 * 5 * 5,加一个偏置项,总:6 * 5 * 5 + 1
-
C3的总训练参数:6 *(3 * 5 * 5 + 1)+ 9 *(4 * 5 * 5 + 1)+6 * 5 * 5 + 1 =1516
网络连接数量:1516 * 10 * 10 = 151600 个
3.4 S4下采样(池化)
- 输入特征图:10 * 10 共16 层C3 特征图
- 采样核:2 * 2 (步长为2)
- 采样核深度:16 (和C3输出特征深度相同)
- 可训练参数:2 * 16
- 网络连接数量:(2 * 2 + 1)* 6 *5 *5
- 输出池化特征图:5 * 5 * 16
C3层输出特征图大小是10 * 10,S4输出是5 *5 ,只有1/4 大小了。
3.5 C5 卷积
这里有120个卷积核,每个卷积核包含16个卷积模板,这样一个卷积核和S4运算一次相当与每个S4的输出特征图都连接了卷积模板。
- 输入:16个 5 * 5 特征图
- 卷积核:5 * 5
- 卷积核深度:120
- 输出特征图:1 * 1 (5 - 5 + 1) 共计120个
- 训练优化的参数:120 * (5 * 5 * 16 + 1)= 48120 个
- 120个卷积核,每个核16个卷积模板,模板是5*5,再加一个偏置
3.6 F6 全连接
这里全连接层有84个神经节点,和C5的120 维神经节点进行全连接。
- 输入:C5卷积输出的120 * 1 * 1的特征
- 输出:84 维的特征。
- 可训练参数:84 * (120 + 1) = 10164
一般会把卷积网络最终输出的N多维向量使用 softmax 函数转化为概率密度函数。之后可以作为分类判断,也可以结合样本ylabel求解交叉熵。
4 网络优化改进方向
4.1 输入数据的处理
- Normallization 归一化
- 输入数据中心式均值归一(移除共同,凸显差异)
- 数据扩充
- 水平翻转、旋转(-30, -15,15, 30)
- 随机扣取(原图0.8-0.9)
- 尺度变换(图像分辨率0.8, 0.9, 1.1, 1.2, 1.3)
- 色彩抖动(RGB微调色值,HSV微调SV值)
- 监督式数据扩充(绘制热力图特征图看相关性,扣取有关的)
- 训练数据随机打乱(shuffle):配合Mini_batch
- 不平衡样本:有的类别很多,有的类别极少
- 数据少的(over_sampling),多的(under-sampling)
- 类别平衡采样:先随机取类,再从类里抽样
- 算法层面:根据混淆矩阵添加代价敏感矩阵、向量
4.2 网络参数的处理
4.2.1网络训练参数初始化:
- 随机初始化(高斯、去偏离正态、均匀分布等)
- 全零初始化
- 获得预先训练好的模型参数
4.2.2 Regularization 正则化
给参数加权重,加快收敛,防止过拟合。
参考博客:链接1 链接2
- L1正则:∑|W|(Lasso)
- L2正则:Ridge Regression(岭回归)权重衰减
4.2.3 神经元随机失活:
被drop的只是本轮不参与训练,下轮可能就会参与。
- Dropout:模型训练时随机让网络某些隐含层节点的权重不起作用,但是它的权重保留下来(只是暂时不更新)
- DropConnect:不像DropOut一样随意设置输出节点的值为0,而是随机设置权重矩阵W 为0。
4.2.4 学习率learning rate
不宜过大,0.01和0.001为佳。一般都设为0.001
- 指数衰减(较常用)
- 轮数衰减
- 分数衰减
知乎专栏:
4.3 卷积层的优化
一个大卷积层替换为多层小卷积层结构:
- L到L+1层映射关系为1 * 1——7 * 7和L层——L+3层中间包含3层3 * 3 相比平添了很多卷积核的优化参数,效果却近似,所以小而多的卷积层较好。
- 添加中间层小卷积核增强了网络容量和复杂度,降低了卷积参数个数。
- 配合填充(padding):利用处理边缘信息、保证图像大小
1*1 的卷积核的作用:
-
改变特征图深度:升、降维(改通道数)、明显降低计算量
-
增加非线性:提高表达能力。
参考博客:1*1卷积CSDN 知乎回答
4.4 池化层的优化
一般采用 2*2, 3 *3 较小的核,不丢弃过多。
- 常用的一般池化:Max、Mean pooling
- Mixed pooling:混合最大和均值池化
- 随机stochastic pooling:
- Spatial pyramid pooling:金字塔池化
4.5 激活函数的优化
现在最常用的非线性激活函数有relu,relu常见于卷积层。其他sigmoid/tanh比较常见于全连接层,都会或多或少有梯度爆炸或者梯度消失的问题。为了改进relu的死区问题还出现了几种衍生算法,一般不常用。
- sigmoid:值域在[0,1]之间,过大过小x时梯度为零,误差无法前传
- tanh:值域在[-1,+1],容易和sigmoid类似梯度饱和(爆炸)或消失
- ReLU(有死区,x<0,梯度为0)
- LReLU : x<0时加参数 α ,防死区
- PReLU
- RReLU(随机化)
- 指数化线性单元(ELU)
4.6 损失函数的优化
回归问题:
- 普通残差:y_pre-y
- L1损失:∑|残差|
- L2损失:∑|残差|2
分类问题:
- Softmax loss :交叉熵损失函数,卷积网络最常用
- Hinge loss:像SVM类似的大边距。
- Robust loss:
- 大间隔交叉损失:large-margin softmax loss
- 中心损失:center loss
4.7 优化器的选择
普通的梯度下降法在神经网络里不常使用,因为参数太多,无法同时更新所有的参数。
- 随机梯度下降(Stochastic gradient descent)
- 动量更新:(MomentumOptimizer)
- AdamOptimizer、AdadeltaOptimizer等等
其他常用的可以在tensorflow.train.里面查看。知乎专栏
5 应用场景
- 图像分类
- 物体跟踪
- 身体姿态估计
- 文本检测
- 动作识别
- 场景标记
感谢:魏秀参博士-解析卷积神经网络的电子书以及众多优秀的博客作者。