单源最短路径:Dijkstra算法
一,Dijkstra算法基本概念
Dijkstra算法使用了广度优先搜索解决非负权有向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
该算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。我们以 V 表示图 G 中所有顶点的集合。每一个图中的边,都是两个顶点所形成的有序元素对。(u, v) 表示从顶点 u 到 v 有路径相连。我们以 E 表示G中所有边的集合,而边的权重则由权重函数 w: E → [0, ∞] 定义。因此,w(u, v) 就是从顶点 u 到顶点 v 的非负权重(weight)。边的权重可以想像成两个顶点之间的距离。任两点间路径的权重,就是该路径上所有边的权重总和。已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t的最低权重路径(例如,最短路径)。这个算法也可以在一个图中,找到从一个顶点 s 到任何其他顶点的最短路径。对于不含负权的有向图,Dijkstra算法是目前已知的最快的单源最短路径算法。
1,算法步骤:
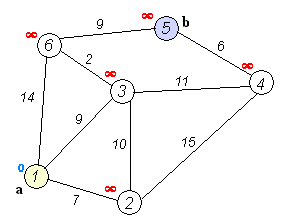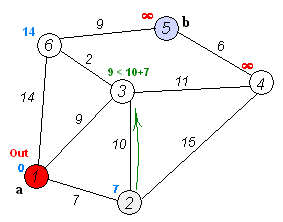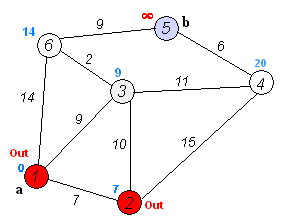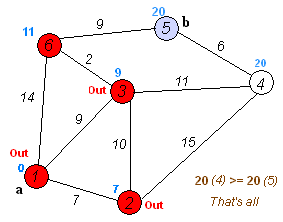
1). 初始时令 S={V0},T={其余顶点},T中顶点对应的距离值,若存在,d(V0,Vi)为弧上的权值,若不存在,d(V0,Vi)为∞。
2). 从T中选取一个其距离值为最小的顶点W且不在S中,加入S。
3). 对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值。
4).重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止。
动画演示如下
二,C++模板实现
1,Graph.h代码如下(无向图):
#include "stdafx.h"
#include "iostream"
using namespace std;
template *m_pnext;//下一条边(注意不是下一个顶点,因为m_nposTable已经知道了这个顶点的位置)
};
//声明
template *pmove = padjEdge;
while (pmove)
{
padjEdge = pmove->m_pnext;
delete pmove;
pmove = padjEdge;
}
}
private:
friend class Graph;//允许Graph类任意访问
NameType m_vertexName;//顶点中的数据内容
Edge *padjEdge;//顶点的邻边
};
template[size]; //为顶点集分配内存
if (m_pVertexTable == NULL)
{
exit(1);
}
m_numVertexs=0;
m_nmaxSize=size;
m_nnumEdges=0;
}
~Graph()
{
Edge *pmove;
for (int i=0; i < this->m_numVertexs; i++)
{
pmove = this->m_pVertexTable[i].padjEdge;
if (pmove){
this->m_pVertexTable[i].padjEdge = pmove->m_pnext;
delete pmove;
pmove = this->m_pVertexTable[i].padjEdge;
}
}
delete[] m_pVertexTable;
}
int GetNumEdges()
{//获得边的数目
return m_nnumEdges/2;
}
int GetNumVertexs()
{//获得顶点数目
return m_numVertexs;
}
bool IsGraphFull() const
{ //图满的?
return m_nmaxSize == m_numVertexs;
}
//在顶点集中位置为v1和v2的顶点之间插入边
bool InsertEdge(int v1, int v2, DistType weight=m_Infinity);
//插入顶点名字为vertex的顶点
bool InsertVertex(const NameType vertex);
//打印图
void PrintGraph();
//顶点v到其他各个顶点的最短路径(包括自身)
void Dijkstra(int v, DistType *shotestpath);
//获取顶点集中位置为v1和v2的顶点之间边的权重值
DistType GetWeight(int v1, int v2);
//获得在顶点集中的位置为v的顶点的名字
NameType GetVertexValue(int v);
//用该顶点的名字来寻找其在顶点集中的位置
int GetVertexPosTable(const NameType vertex);
private:
Vertex *m_pVertexTable; //顶点集
int m_numVertexs;//图中当前的顶点数量
int m_nmaxSize;//图允许的最大顶点数
static const int m_nDefaultSize = 10; //默认的最大顶点集数目
static const DistType m_Infinity = 65536; //边的默认权值(可以看成是无穷大)
int m_nnumEdges;//图中边的数目
};
//返回顶点vertexname在m_pVertexTable(顶点集)中的位置
//如果不在顶点集中就返回-1
template
int Graph::GetVertexPosTable(const NameType vertexname)
{
for (int i=0; i < this->m_numVertexs; i++)
{
if (vertexname == m_pVertexTable[i].m_vertexName)
{
return i;
}
}
return -1;
}
//打印图中的各个顶点及其链接的边的权重
template
void Graph::PrintGraph()
{
Edge *pmove;
for (int i=0; im_numVertexs; i++)
{
cout << this->m_pVertexTable[i].m_vertexName << "->";
pmove = this->m_pVertexTable[i].padjEdge;
while (pmove)
{
cout << pmove->m_distWeight << "->" << this->m_pVertexTable[pmove->m_nposTable].m_vertexName << "->";
pmove = pmove->m_pnext;
}
cout << "NULL" << endl;
}
}
//获得在顶点集中的位置为v的顶点的名字
template
NameType Graph::GetVertexValue(int v)
{
if (v<0 || v>=this->m_numVertexs)
{
cerr << "查找的顶点位置参数有误,请检查!" <
DistType Graph::GetWeight(int v1, int v2)
{
if (v1>=0 && v1m_numVertexs && v2>=0 && v2m_numVertexs)
{
if (v1 == v2)
{
return 0;
}
Edge *pmove = m_pVertexTable[v1].padjEdge;
while (pmove)
{
if (pmove->m_nposTable == v2)
{
return pmove->m_distWeight;
}
pmove = pmove->m_pnext;
}
}else
{
return m_Infinity;
}
}
//顶点依次插入到分配好的顶点集中
template
bool Graph::InsertVertex(const NameType vertexname)
{
if (IsGraphFull())
{
cerr<<"图已经满,请勿再插入顶点!"<m_pVertexTable[this->m_numVertexs].m_vertexName = vertexname;
this->m_numVertexs++;
}
return true;
}
//在顶点集位置为v1和v2的顶点之间插入权值为weght的边(务必保持输入的准确性,否则.....)
template
bool Graph::InsertEdge(int v1, int v2, DistType weight)
{
if (v1 < 0 && v1 > this->m_numVertexs && v2 < 0 && v2 > this->m_numVertexs)
{
cerr<<"边的位置参数错误,请检查! "< *pmove = m_pVertexTable[v1].padjEdge;
if (pmove == NULL)//如果顶点v1没有邻边
{ //建立顶点v1的第一个邻边(该邻边指明了目的顶点)
m_pVertexTable[v1].padjEdge = new Edge(v2, weight);
m_nnumEdges++;//图中边的数目
return true;
}else//如果有邻边
{
while (pmove->m_pnext)
{
pmove = pmove->m_pnext;
}
pmove->m_pnext = new Edge(v2, weight);
m_nnumEdges++;//图中边的数目
return true;
}
}
}
//Dijkstra单源最短路径算法
template
void Graph::Dijkstra(int v, DistType *shPath)
{
int num =GetNumVertexs();
int *visited = new int[num];
for (int i=0; i < num; i++)
{//初始化
visited[i] = 0;//未访问
shPath[i] = this->GetWeight(v, i);//顶点v(当前中间点)到各个相邻顶点的边权值,其他情况返回无穷大
}
visited[v] = 1;//第v个顶点初始化为被访问,并以他为中点点开始找最短路径
for (int i = 1; i < num; i++)
{
DistType min = this->m_Infinity;
int u=0;
//寻找新的中间点u,依据就是数组中权值最小的那个点的位置(且没被访问过)
for (int j=0; j < num; j++)
{
if (!visited[j])
{
if (shPath[j]GetWeight(u, w);//顶点u(当前中间点)到各个相邻顶点的边权值,其他情况返回无穷大
if (!visited[w] && weight != this->m_Infinity )
{
if ( shPath[u]+weight < shPath[w] )
{
shPath[w] = shPath[u] + weight;//更新顶点v到w的最短路径值
}
}
}
}
delete[] visited;
} 2,主测试代码如下:
// ConsoleAppMyGraph.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "Graph.h"
#include
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
Graph graph(7);
char *vertex[7] = {"【地大】", "【武大】", "【华科】", "【交大】", "【北大】", "【清华】", "【复旦】"};//顶点集
for (int i=0; i<7; i++)
{
graph.InsertVertex(vertex[i]);
}
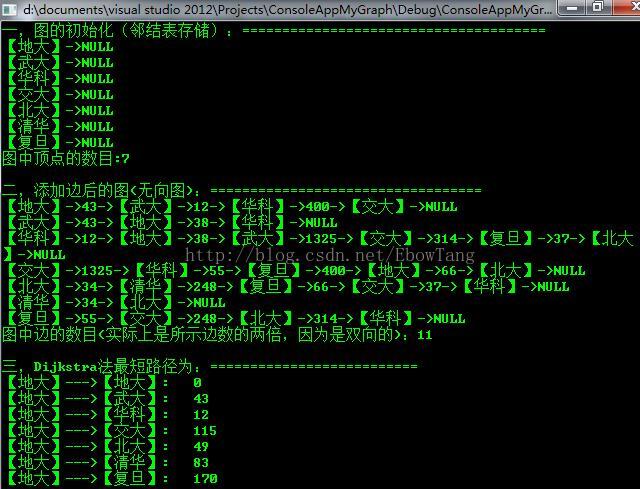
cout<<"一,图的初始化(邻结表存储):======================================"<" << graph.GetVertexValue(i)
<< ": " << shortestPath[i] < 3,测试结果如下:
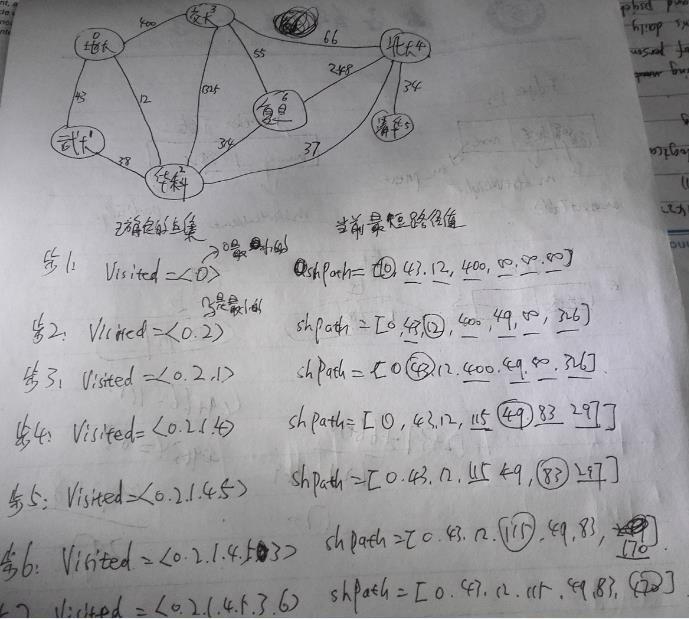
4,其中的计算过程如下:
邻接矩阵的代码:
本代码还设定了必经点。
#include
#include
#include
#include
using namespace std;
int dijkstra(int(*graphy)[8], int vertexs, int s_v, int e_v, int *path, int *ban_visit);
int _tmain(int argc, _TCHAR* argv[])
{
system("color 0A");
int g[8][8];
memset(g, -1, sizeof(int)* 8 * 8);
for (int i = 0; i < 8; i++)
g[i][i] = 0;
g[1][2] = 3, g[2][1] = 3;
g[1][6] = 1, g[6][1] = 1;
g[2][3] = 2;
g[2][4] = 1;
g[4][3] = 3;
g[3][5] = 1;
g[3][6] = 1;
g[7][3] = 3;
g[5][4] = 1;
g[5][7] = 2;
int path[8] = { 0 };
int shortestdist;
int mustpass[4] = {2,3,4,7};
int ban_visit[10] = {0};
ban_visit[5] = 1;
for (int i = 0; i < 3; i++)
{
int start_vertex = mustpass[i];
int end_vertex = mustpass[i+1];
shortestdist = dijkstra(g, 8, start_vertex, end_vertex, path, ban_visit);
if (shortestdist != -1)
{
cout << "shortest path, from " << start_vertex << " to " << end_vertex << " is: " << shortestdist << endl;
cout << "path: ";
for (int i = end_vertex; path[i] != -1; i = path[i])
cout << i << "<--";
cout << start_vertex << endl << endl;
}
else
cout << "shortest path, from " << start_vertex << " to " << end_vertex << " is not exist." << endl << endl;
}
system("pause");
return 0;
}
// 最短路径:Dijkstra, dist[j] = min{dist[j], dist[i]+graphy[i][j]}
// graphy: G = (V, E), V:顶点集, E: 边集
// e ∈ E & e > 0表示顶点邻接,权值为e, e = -1表示两顶点不邻接
//
int dijkstra(int(*graphy)[8], int vertexs_nums, int start_vertex, int end_vertex, int *path, int *ban_visit)
{
int *shortpath = new int[vertexs_nums];; //存储起点到各终点的最短路径
int *visited = new int[vertexs_nums];; //已访问过的顶点
int num;
int min, k;
//初始化,-1代表max_value
memset(shortpath, -1, sizeof(int)*vertexs_nums);
//起点到终点最短距离为0
shortpath[start_vertex] = 0;
memset(visited, 0, sizeof(int)*vertexs_nums);
memset(path, -1, sizeof(int)*vertexs_nums);
num = vertexs_nums - 1;
while (num)
{
//贪心策略:从访问过的顶点中,找出最短路径,从已知的最短路径开始延伸
//寻找新的中间点k,依据就是数组中权值最小的那个点的位置(且没被访问过)
min = -1;
k = -1;
for (int i = 0; i min + graphy[k][i] || shortpath[i] == -1))
{
shortpath[i] = min + graphy[k][i];
path[i] = k; //更新记录前驱顶点,供最后回溯最短路径
}
}
}
min = shortpath[end_vertex];
delete[] shortpath;
delete[] visited;
return min;
} 参考资源:
【1】《算法导论》
【2】《维基百科》
【3】《百度百科》
【4】https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm【5】http://blog.csdn.net/todd911/article/details/9347053
注:
本文部分文字学习并copy自网络,代码转载并改写于网络资源.
如果侵犯了您的版权,请联系本人[email protected],本人将及时编辑掉!