自然语言处理NLP（3）——神经网络语言模型、词向量

在上一部分中，我们了解到了统计语言模型，n-gram模型以及语料库的基本知识：
自然语言处理NLP（2）——统计语言模型、语料库
在这一部分中，我们将在此基础上介绍神经网络语言模型以及词向量的相关知识。
在介绍这些知识之前，我们首先对自然语言处理领域的整体架构进行一些简单的介绍。

【一】自然语言处理架构

首先，我们来看这样一张图。

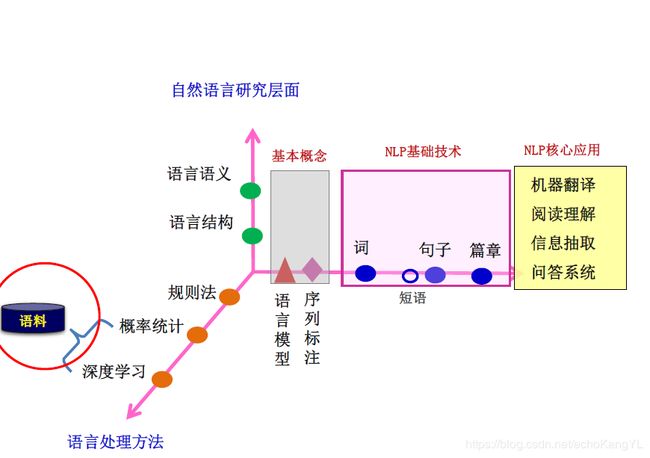
从这张图中，可以清晰地看到，所谓的规则法、概率统计法、深度学习法都只是处理各类NLP问题的具体方法，而不是NLP问题的组成部分。
（这一点一定要清晰，NLP不只是深度学习，深度学习仅仅是解决其问题的方法之一）

而具体的NLP问题包括对于词、短语、句子、篇章的处理问题，以及NLP的一些应用问题：例如机器翻译、阅读理解、信息抽取、问答系统等。这一切的问题都包括两个层次：结构、语义。目前来说，对于语义的把握要更难。
解决这些问题离不开两个基本概念：语言模型、序列标注。语言模型的概念我们在之前的介绍中已经有提到过，序列标注的概念我们将在今后的章节进行介绍。
所以，这张图传递给我们的核心信息就是：利用规则法、概率统计法、深度学习法来解决各类NLP问题。方法可能有所不同，但是NLP问题才是核心。

了解了这一点，我们开始下一个方面的介绍——神经网络语言模型。

【二】神经网络语言模型

在上一节：自然语言处理NLP（2）——统计语言模型、语料库，我们已经了解了什么是语言模型（n-gram），以及什么是语言模型中的参数（P(S)等式中的各个P值）。传统语言模型利用概率统计法求取语言模型参数，而神经网络语言模型，就是利用神经网络求取这些语言模型参数。

为什么要用神经网络？
在了解统计语言模型之后，不难发现，统计语言模型具有这样的缺点：
1.平滑技术错综复杂，而且会使得模型回退到低阶，使得模型无法面向更大的n元文法获取更多的词序信息。
2.基于极大似然估计（MLE）的统计语言模型缺乏对上下文的泛化。例如，观察到black car和blue car不会影响到对red car的估计。
而神经网络语言模型将很好地解决这两个问题。

在对神经网络语言模型进行介绍之前，我们需要对各种神经网络有所了解。
本人的另一篇博客中对NLP领域常用的神经网络进行了介绍，对神经网络不太了解的朋友们可以自行学习：神经网络基础：DNN、CNN、RNN、梯度下降、反向传播

根据所使用的神经网络不同，神经网络语言模型分为两种：
1.NNLM（利用DNN）
2.RNNLM（利用RNN）

（一）NNLM

为了方便叙述，在这里首先以2-gram为例，假设统计基元为词。
先来回顾一下上一部分的内容：在语言模型中，2-gram可以写成这样的式子：
$$P(w_1,w_2,...,w_m)=\prod _{i=1}^{m}P(w_i|w_{i-1})$$
换成通俗语言来讲就是：已知当前词前面的一个词，预测当前词。

NNLM语言模型如下：

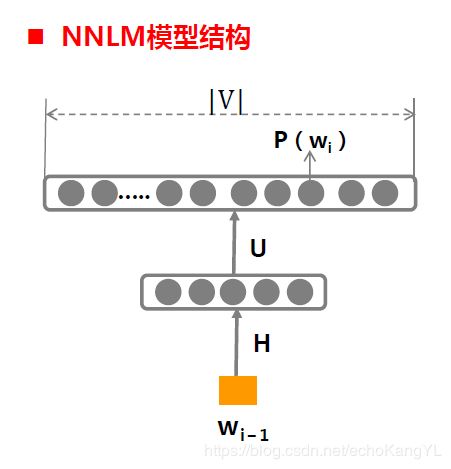
不要忘了，对于一个模型来说最重要的是什么？
四元组：输入、输出、参数、对应运算关系

在NNLM中，
输入为X：$w_{i-1}$，即当前词的前一个词；
输入为Y：$P(w_i|w_{i-1})$，即基于前一个词所预测出来的当前词概率；
而且，这个东西就是语言模型的参数啊！
参数：$\theta =\{H,U,b^1,b^2\}$，图中描述很清晰，在这里就不进行解释了；
在这里，参数是指神经网络的参数，而不是语言模型的参数。
运算关系：
$$y(w_i)=b^2+U(tanh(XH+b^1)$$
$$P(w_i|w_{i-1})=\frac{exp(y(w_i))}{{\sum }_{k=1}^{|V|}exp(y(w_k))}$$
第一个式子很好理解，其中激活函数为tanh函数；
第二个式子是一个softmax，将输出转化为概率，其中，$|V|$是词汇表大小（即，当前词共有多少种可能）。

模型的学习过程与DNN的学习过程类似，这里不再赘述，有需要的朋友可以参考：神经网络基础：DNN、CNN、RNN、梯度下降、反向传播

于是，在我们利用NNLM预测某句话出现的概率的时候，就成了这个样子：

可以看出，每一步预测时，输入前一个词，找到输出中当前词所对应的概率（即语言模型参数），对整个句子进行这样的操作过后，将概率值累乘，即可得到最终结果。

对于n-gram模型，有公式如下：
$$P(w_1,w_2,...,w_m)=\prod _{i=1}^{m}P(w_i|w_{i-(n-1)}...w_{i-1})$$
于是很自然地，模型结构如下：

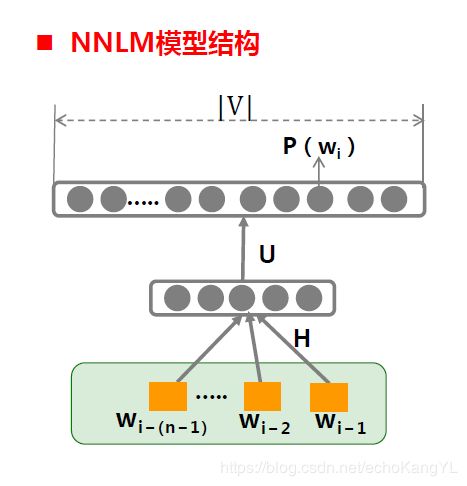
可以看出，相较于2-gram，模型输入部分改变为X：$w_{i-(n-1)},...w_{i-2},w_{i-1}$，输出部分改变为Y：$P(w_i|w_{i-(n-1)}...w_{i-1})$，其余部分不变。

于是，模型预测过程变化为：

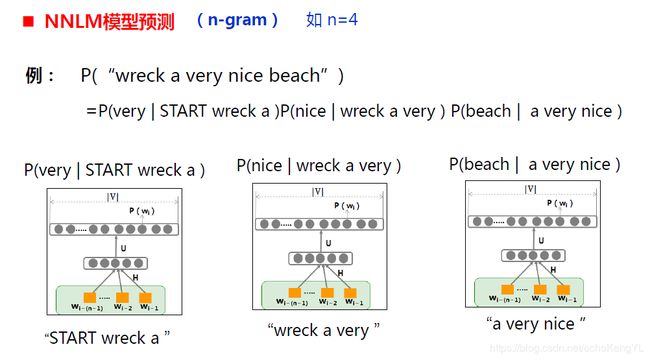
与2-gram类似，这里不再进行过多解释。

（二）RNNLM

相较于NNLM，利用RNN构建的RNNLM基本结构如下：

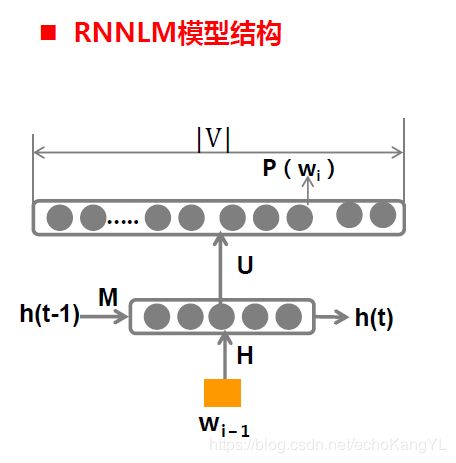
还是那个老问题，模型最基本的四元组是什么？
输入X：$w_{i-1}$以及上一刻传递而来的$h(t-1)$
输出Y：$P(w_i|w_{i-1})$以及传递给下一时刻的$h(t)$
参数：$\theta =\{H,U,M,b^1,b^2\}$，图中描述也很清晰，同样不再进行解释；
运算关系：
$$h(t)=tanh(XH+Mh(t-1)+b^1)$$
$$y(w_i)=b^2+U(tanh(XH+Mh(t-1)+b^1)$$
$$P(w_i|w_{i-1})=\frac{exp(y(w_i))}{{\sum }_{k=1}^{|V|}exp(y(w_k))}$$
与RNN的基本运算关系类似，在这里不进行过多解释，有兴趣的朋友可以参考：神经网络基础：DNN、CNN、RNN、梯度下降、反向传播

与NNLM相比，RNNLM多了一个内部隐层h(t)，整个h(t)有什么用呢？
我们先把这个问题放下，不过我们不会等太久，马上就会对这个问题进行解释。

RNNLM模型的学习过程与一般的RNN学习过程类似，有兴趣的朋友同样可以参考上述博客：神经网络基础：DNN、CNN、RNN、梯度下降、反向传播

RNNLM模型的预测过程如下：

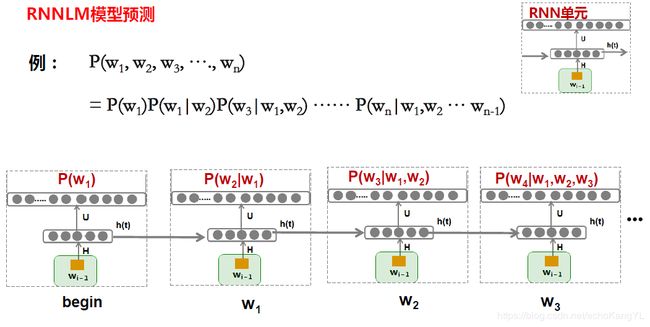
看到这里，是不是忽然明白了我们之前留有疑惑的一个问题：h(t)的作用是什么？

因为有h(t)的存在，整个网络保留了上文信息（对于双向RNN来讲，保留了上下文信息），这样可以每次只输入一个词，就可以模拟n-gram。
而在NNLM中，模拟n-gram需要输入n-1个词。
这样，RNNLM保留了更丰富的上文信息，有潜力达到更好的效果。

【三】神经网络词向量

在使用深度学习技术解决自然诧言处理任务时，最基础的问题是词的表示。

回顾上面介绍过的NNLM模型和RNNLM模型，无论那种模型，都建立在神经网络的基础之上。而在神经网络中，模型的输入、输出都需要是向量，那么如何把词输入神经网络呢？换句话说，用什么样的向量表示一个“词”呢？
这就是词的表示问题。

自然语言问题要用计算机处理时，第一步要找一种方法把这些符号数字化，成为计算机方便处理的形式化表示。
于是，词的表示问题成了最初需要解决的问题。

词的向量表示分为两种：离散表示和分布式表示。
1.离散表示：
（1）one-hot
这是NLP中最直观、最常用的表示方法。例如，
减肥：[0 0 0 0 1 0 0 0 0 0 0 0]
瘦身：[0 0 0 0 0 0 0 0 0 1 0 0]

one-hot的优势在于：稀疏存储的方式非常简洁；
缺点在于：相似词之间的距离不会更近——词汇鸿沟；
词语个数太多，表示每个词的维度太多——维数灾难。

（2）词袋模型
语料库中one-hot的加和。

（3）TF_IDF
每个数代表该词在整个文档中的占比。

这里，对于三种方法的描述没有太多细节，有兴趣的朋友们可以自行百度了解~

2.分布式表示：
分布式表示的核心思想是：利用一个词附近的其他词来表示该词。

神经网络词向量就是一种基于预测的分布式表示方法，用“基于词的上下文词来预测当前词”或“基于当前词预测上下文词”的方法构造低维稠密向量作为词的分布式表示 。

介绍了神经网络词向量的背景和概念之后，我们来看看词向量在模型中究竟怎么用。

加入了词向量的NNLM与原始NNLM相比有了这样的变化：

图中，左边是我们之前提到过的NNLM，右边是加入了词向量的NNLM。
（该模型模拟n-gram）

很容易可以看出，词是通过一个look-up表转化为词向量的，我们将这个look-up表称为表C。换句话说，look-up表C将原始文本（one-hot形式）转化为D维稠密词向量。

look-up表C是这个样子的：

look-up表C是一个$|D|\ast |V|$维实数投影矩阵，其中，$|D|$表示词向量e的维度（一般为50维以上），$|V|$表示词表大小。
意味着词表中每一个词都由一个$|D|$维向量表示。
各词的词向量存于look-up表C中。词$w$到其词向量$e(w)$ 的转化是从该矩阵中取出相应的列。

例如，
$w_2$的one-hot表示为：$w_2$ = [0 1 0 0 … 0]
那么从表C中选取第二列，$w_2$的向量表示就是：
$e(w_2)=(w_2{)}_1(w_2{)}_2...(w_2{)}_D$

于是，原始文本就可以转化为向量形式输入模型之中了。

在这里，仔细想想，我们可以发现，如果将词向量赋予一个随机初值，那么词向量可以作为模型的参数通过训练得到！

有没有一点理解呢？
没有的话让我们来仔细解释一下：
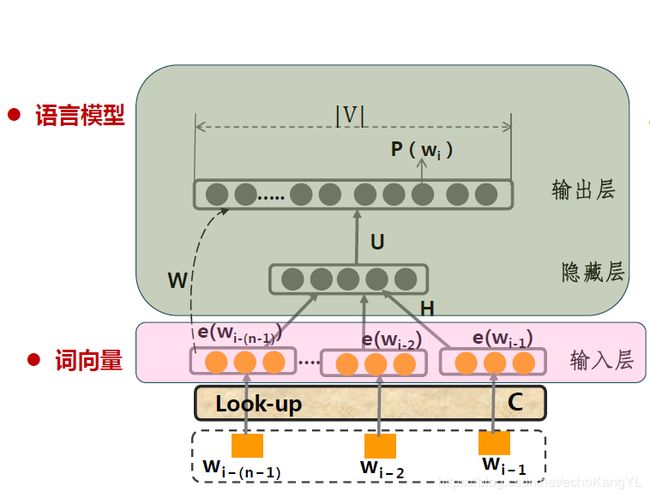
这是加入了词向量之后NNLM的模型结构：

（图中最左侧这条权重为W的连边并不重要）
还是老问题，四元组是什么？
由于我们试图想要利用模型训练得到词向量，所以相较于上面提到的NNLM模型有所不同：
输入$X$：$X=[e(w_{i-(n-1)})...e(w_{i-1})]$（词向量的初始随机值）
输出Y：$P(w_i|w_{i-(n-1)}...w_{i-1})$（与原先的n-gram相同）
参数：$\theta =\{H,U,M,b^1,b^2,$ 词向量$\}$
运算关系：
$$y(w_i)=b^2+WX+U(tanh(XH+b^1)$$
$$P(w_i|w_{i-(n-1)}...w_{i-1})=\frac{exp(y(w_i))}{{\sum }_{k=1}^{|V|}exp(y(w_k))}$$
运算关系中，加入了最左边权重为W的连边所造成的影响，但是这个部分并不重要，朋友们不必太过纠结。

在这里，词向量也是模型中的参数，随着模型的迭代进行调整。
这样，训练结束过后，我们就得到了我们想要的词向量。
也就是说，词向量和语言模型参数，都是我们所求的目标。

我们学得的词向量具有如下的语言学特征：
1.语义相似的词，其词向量空间距离更相近

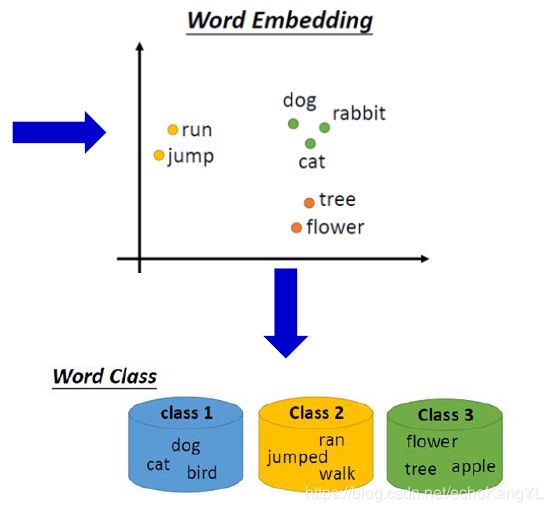
2.相似关系词对的词向量之差也相似

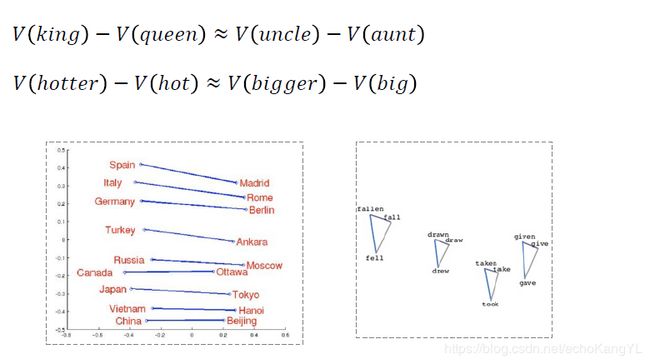
这些词向量的语言学特征可以用来完成语义相关任务，例如：
$Rome:Italy=Berlin:?$
直接使用词向量的加减法（因为相似关系词对的词向量之差也相似），可以得到：
$V(Germany)\approx V(Berlin)-V(Rome)+V(Italy)$

RNNLM词向量的训练过程与NNLM相似，这里就不再赘述。

此外，对CBOW、C&W、Skip-gram模型训练词向量感兴趣的朋友们可以自行百度进行了解~

词向量模型可以从大规模无标注语料中自动学习到句法和语义信息，基于词向量的神经网络模型也为多项NLP任务带来了性能的提升，在深度学习自然语言处理技术中，词向量是重要的组成部分。

现在，我们对神经网络语言模型、词向量这些NLP领域最基本的知识有了一定的了解，在下一部分的内容中，我们将正式接触NLP领域的第一个问题——序列标注。

如果本文中某些表述或理解有误，欢迎各位大神批评指正。

谢谢！