1.4.1 机器学习基础
深度学习是机器学习的一个分支。
机器学习
机器学习是一门研究‘学习算法’的学问,所谓学习是指对于任务T和性能度量P,一个计算机程序能够在T上以P衡量的性能随着经验E而自我完善,那我们称这个计算程序在从经验E中学习。
任务T :机器学习应该如何处理样本,样本是指机器学习系统处理的对象或者事件已经量化的特征集合。 (分类,回归,机器翻译)
性能度量P:评估机器学习算法的能力。
模型评估的基本参数:
1、阳性数据P(关注的数据,在医院阳性结果),阴性数据N(不关注的数据)
真阳性:本身为阳性被正确判断阳性 TP
真阴性:本身为阴性被正确判断阴性 TN
伟阳性:本身为阴性被错误判断阳性 FP
伟阴性:本身为阳性被所悟判断阴性 FN

2、精度 precision : TP/(TP+FP)
3、召回率recall (敏感度,真正比例) : TP/P
4、准确率(识别率) : (TP+TN)/(P+N)
5、AUC : 要先知道ROC曲线,ROC曲线是FP rate 和 TP rate之间的线性关系图, AUC是ROC曲线下面积
如果机器判断结果正确和错误是1:1 ,AUC=0.5,也就是AUC<0.5表示模型不可用,只有AUC>0.5模型才可用
6、 F1 测量值是精确率和召回率的加权平均值
F 1 = ( 2 ∗ p r e c i s i o n ∗ r e c a l l ) / ( p r e c i s i o n + r e c a l l ) F1 = (2*precision*recall)/(precision+recall) F1=(2∗precision∗recall)/(precision+recall)
类不平衡:阳性和阴性数据差别很大
比较参数顺序: AUC–>阳性和阴性–>F1–>精确、召回–>准确率
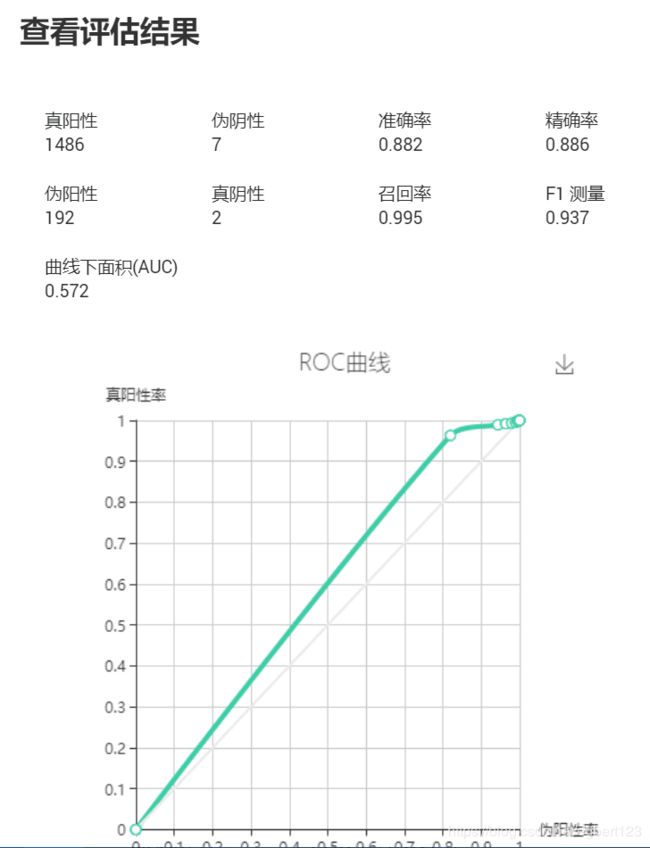
例如:
首先我们从机器的AUC值上来看,AUC代表的是机器判断的整体准确性,小于0.5代表该机器绝对不可用。本分析结果AUC=0.572,模型可用。
在阳性和阴性数据的判断上,我们可以发现,机器的判断基本都将数据判断为阳性数据,而忽略了阴性数据的存在,这本身就是出现了类不平衡的问题。
另外从伪阳性上看,我们可以发现,在一共194个阴性数据中,机器只判断出了9个其所认为的阴性数据,并且正确的只有2个。所以机器对于阴性数据的查找是非常差的,这种性能上的缺失除了会影响阴性数据的判断,还会影响阳性数据的准确度和其他相关的参数。
从F1的角度上来看,为0.937整体参数优秀。
精确率和召回率都在非常高的范围,但是由于阳性和阴性数据的判断出现了误差,所以这些参数并不是非常的可信。
准确性0.882还是处于比较优秀的状态。
综上所述,我们认为该模型如果在阳性数据和阴性数据区别不大的情况下可以使用,但是建议谨慎选择。
经验E : 大部分学习算法被认为是在整个数据集上获取经验,有些算法的数据集并不固定,例如强化学习会和环境互动。机器学习算法根据学习过程中经验的不同可以分为监督算法和无监督算法。
容量,过拟合,欠拟合
泛化能力: 在未观测数据下的表现良好的能力
数据集
训练集:60%
验证集:20% :通过验证集或简单交叉验证集选择最好的模型
测试集:20% :目的是对最终选定的神经网络系统做出无偏差估计,如果不需要无偏差估计,可以不需要测试集
数据很大时:98/1/1
保证训练集和测试集来自相同的来源
用来评估偏差和方差的关键数据是:训练误差和验证集误差
过拟合
Train set error: 1%
Dev set error : 11%
在训练集表现良好,在验证集表现很差,可能某种程度上验证集并没有充分利用交叉验证集的作用,这种情况称为 ‘高方差’ high variance
欠拟合
Train set error: 15%
Dev set error : 16%
假设这个案例中人的错误率是0%, 模型在训练集表现很差,如果数据的拟合度不高,这种情况称为 ‘高偏差’ high bias
Train set error: 15%
Dev set error : 30%
high bias and high variance
Train set error: 0.5%
Dev set error : 1%
low bias and low variance
从预先知道的真实分布p(x, y)而出现的误差也被称为贝叶斯误差接近0%,所以如果最优误差是15%, 那么模型在train set error是15%,我们也任务low bias and low variance
在训练集上的表现体现在偏差上 bias
在验证集上的表现体现在方差上variance
正则化
正则化是指我们修改学习算法,使其降低泛华误差而不是降低训练误差。
机器学习算法的效果不仅很大程度上受影响于假设空间的函数数量,也取决于这些函数的具体形式。
对于线性模型,我们可以加入权重衰减来修改线性回归的训练标准 J ( w ) = M S E t r a i n + λ w T w J(w) = MSE_{train} + \lambda w^Tw J(w)=MSEtrain+λwTw
其中 λ \lambda λ是提前选出的值(超参数),当 λ = 0 \lambda = 0 λ=0时,我们没有任何偏好,越大的 λ \lambda λ偏好范数越小的权重。最小化 j ( w ) j(w) j(w)可以看做是你和训练数据和偏好小权重范数之间的权衡。这会让斜率更小,或者将权重放在较小的特征上。
超参数和验证集
省略
交叉验证
常见的是k-折交叉验证算法,将数据集分为K个不同不重合的子集,测试误差可以估计为K次计算后的平均测试误差,在第i次测试时,数据的第i个子集用于测试集,其它的数据用于训练集。

估计、偏差和方差
偏差和方差度量这估计量的两个不同误差来源,偏差度量着偏离真是函数或参数的误差期望,而方差度量着数据上任意特定采样可能导致的估计期望的偏差。
最大似然估计(参数估计)
频率派统计: 基于估计单一值 θ \theta θ的方法,然后基于该估计作出所有的预测。
一个准则,可以让我们从不同模型中得到特定函数作为好的估计,而不是猜测某些函数可能是好的估计,然后分析其偏差和方差。
离散型随机变量:
设总体X是离散型随机变量,概率分布为
P ( X = t i ) = p ( t i , θ ) P(X = t_i)=p(t^i,\theta) P(X=ti)=p(ti,θ)
其中 θ \theta θ是待估计参数
设 X 1 , X 2 , . . . , X n X_1, X_2, ..., X_n X1,X2,...,Xn是来自总体x的样本, x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn是样本值
称函数 L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = ∏ i = 0 n p ( x i ; θ ) L(\theta) = L(x_1, x_2, ..., x_n; \theta) = \prod_{i=0}^np(x_i; \theta) L(θ)=L(x1,x2,...,xn;θ)=∏i=0np(xi;θ)为样本的似然函数。
如果有 θ ′ \theta' θ′使得, L ( θ ′ ) = m a x L ( θ ) L(\theta') = max L(\theta) L(θ′)=maxL(θ),那么称改 θ ′ \theta' θ′为未知参数 θ \theta θ的最大似然估计值。
例如,假设你射箭的命中率为p,那么p符合二项分布,其概率 C n k p k ( 1 − p ) n − k C_n^k p^k (1-p)^{n-k} Cnkpk(1−p)n−k
假设你有三个样本分别是(命中4次概率,命中5次概率,命中6次概率)
构造最大似然函数 L ( p ) = C 10 4 p 4 ( 1 − p ) 6 ∗ C 10 5 p 5 ( 1 − p ) 5 ∗ C 10 6 p 6 ( 1 − p ) 4 L(p) = C_{10}^4p^4(1-p)^6 * C_{10}^5p^5(1-p)^5 * C_{10}^6 p^6(1-p)^4 L(p)=C104p4(1−p)6∗C105p5(1−p)5∗C106p6(1−p)4
使得 L ( p ) L(p) L(p)取得最大值,那么p就是你的命中率

贝叶斯统计
考虑所有可能的 θ \theta θ。