寻找最大流
在大规模战争中,后勤补给是重中之重,为了尽最大可能满足前线的物资消耗,后勤部队必然要充分利用每条运输网,这正好可以用最大流模型解决。如何寻找一个复杂网络上的最大流呢?
直觉上的方案
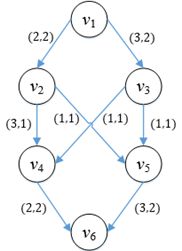
一种直觉上的方案是在一个流网络找到一条从源点到汇点的未充分利用的有向路径,然后增加该路径的流量,反复迭代,直到没有这样的路径为止。广度优先搜索可以在一个流网络中找到这样的路径,这种路径一旦被开充分利用,就会因为达到了最大流量而被“填满”,下次不必再打这条路径的主意。问题是,这样做就一定会得到最大流吗?考虑图下面的网络。
图1
两条明显的路径是v1→v2→v4→v6和v1→v3→v5→v6,依次“填满”两条路径:
图2
此时已经无法再找到新的路径,因此判断最大流是3。然而3并不是最大流,真正的最大流是4:
图3
看来寻找最大流并没有那么简单。为了应对这种情况,需要引入残存网的概念。
残存网
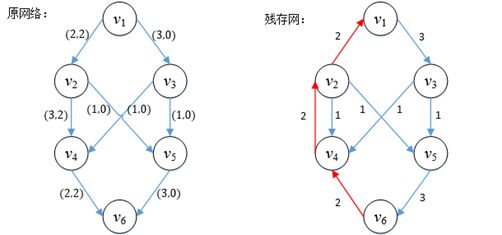
残存网也叫余留网、剩余网,它由原网络中没有被充分利用的边构成。假设有一个流网络G和它的网络流f,G的残存网用Gf表示,我们这样构造一个初始的Gf:Gf和G有同样的顶点,对于原网络中的各条边,Gf将有1条或2条边与之对应,每条边只记录了容量。对于G的一条边v→w,C(v→w)和f(v→w)代表了该边的容量和流量,如果f(v→w)的值为正,则在残存网中包含了一条容量为f(v→w)的边w→v,这条边是原网络中没有的逆向边;如果f(v→w)小于C(v→w),则在残存网中会一条容量为C(v→w)- f(v→w)的边v→w,这条边与原网络同向,它的容量是原网络中v→w的剩余容量;如果原网络中v→w是满边,则残存网中不存在v→w。图8.9展示了一个流网络对应的残存网。
图4
残存网中只记录容量,不记录流量,流量是通过逆向边的容量记录的。由于在原网络中v4→v6是满边,所以残存网中不存在v4→v6,相当于v4→v6的剩余容量用光了,即Cf(v4→v6)=0。由于残存网和原网络存在对应关系,所以增加原网络的流量相当于调整残存网。
增广路径
增广路径是残存网中一条连接源点和汇点的简单有向路径,也称为扩充路径。上图中v1→v3→v5→v6就是一条增广路径。
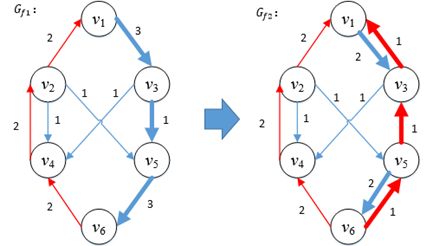
一条增广路径代表着原网络中一条尚未被充分利用的路径,如果想让这条路径得到充分利用,势必会把增广路径上的一条边的剩余容量用完,这样一来,残存网至少会有一条边消失,或直接调转方向:
图5
Gf1上v3→v5的剩余容量被用完,所以在Gf2上删除v3→v5,并增加1条反向的边v5→v3,同时增加另外2条反向边v3→v1和v6→v5,并更新v1→v3和v5→v6的剩余容量。只要增广路径v1→v3→v5→v6得到充分利用,那么原网络上的相应路径也将得到充分利用:
图6
可以看出,原网络的v3→v5已经变成了满边,此时v1→v3→v5→v6也不存在继续扩充的余地。
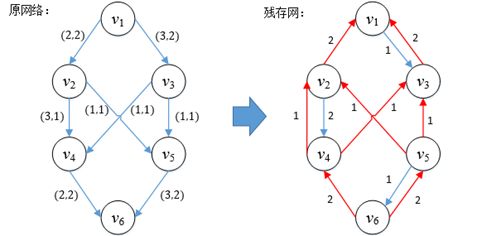
增广路径在告诉我们一个结论,只要把残存网上的增广路径用完,原网络就无法继续扩充,意味着得到了最大网络流。现在,图5残存网Gf2中似乎没有一条连接源点和汇点的路径了,如果就这样结束,则仍然无法找到最大流,怎么办呢?别忘了,残存网中还有逆向边,因此还有一条增广路径,这就是v1→v3→v4→v2→v5→v6,我们填满该路径。
图7
在Gf2中,有1个单位的流量流过v4→v2,这相当于把原来流经v2→v4的流量退还回去,从而获得把退还的流量分配到其他路径的能力。当填满所有的增广路径时,残存网中将不存在从源点到汇点的有向路径,此时原网络中的流值也达到了最大:
图8
增广路径是一条简单路径,路径中的每个顶点只能出现一次,并不是每条连接源点和汇点的有向路径都是增广路径,例如在8.9中,v1→v2→v5是增广路径,v1→v2→v3→v4→v2→v5虽然也连通了源点和汇点,但是v2中这条路径上出现了2次,这条路径并不“简单”,因此不是增广路径:
图9
为什么定义增广路径必须是简单路径呢?以图9的v1→v2→v3→v4→v2→v5为例,设这条路径为P,石油先流入中转站v2,然后绕了一圈后有回到v2,最终统一由v2流向v5。对于v1→v2和v2→v5的容量,无非是两种可能,C(v1→v2)<=C(v2→v5)或C(v1→v2)>C(v2→v5)。
当C(v1→v2)<=C(v2→v5)时,P上能够扩充的流量取决于P上容量最小的边,因此最终扩充的流量一定小于等于C(v1→v2),如果最终扩充的流量小于C(v1→v2),那么v1→v2并没有得到充分利用,中下一次寻径中还会再次找到v1→v2→v5,这还不如一开始就通过v1→v2→v5扩充;与此类似如果最终扩充的流量等于C(v1→v2),也不如一开始就通过v1→v2→v5扩充来得方便。同理,当C(v1→v2)>C(v2→v5)时, 最快的扩充途径仍然是通过v1→v2→v5扩充。可以看出,非简单路径并不是无法得到最大流,只是这样做会增加搜索路径的次数,徒耗钱粮。
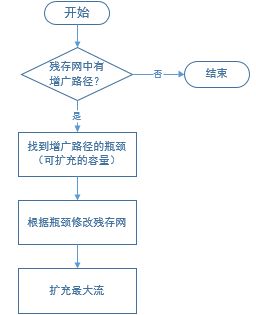
增广路径最大流算法
增广路径最大流算法也称Ford-Fullkerson算法,它通过不断寻找并填满残存网中的增广路径来扩充原网络的流值,直到残存网中不存在增广路径为止:
每填充一条增广路径,就会有这至少一条边被删除或掉转方向,在实际应用中,对于删除的边仅仅是将其容量清零,而并非真正将这条边删除。通过扩展Edge类使之能够表达残存边。
1 class Edge(): 2 ''' 流网络中的边 ''' 3 def __init__(self, v, w, cap, flow=0): 4 ''' 5 定义一条边 v→w 6 :param v: 起点 7 :param w: 终点 8 :param cap: 容量 9 :param flow: v→w上的流量 10 ''' 11 self.v, self.w, self.cap, self.flow = v, w, cap, flow 12 13 def other_node(self, p): 14 ''' 返回边中与p相对的另一顶点 ''' 15 return self.v if p == self.w else self.w 16 17 def residual_cap_to(self, p): 18 ''' 19 计算残存边的剩余容量 20 如果p=w,residual_cap_to(p)返回 v→w 的剩余容量 21 如果p=v,residual_cap_to(p)返回 w→v 的剩余容量 22 ''' 23 return self.cap - self.flow if p == self.w else self.flow 24 25 def moddify_flow(self, p, x): 26 ''' 将边的流量调整x ''' 27 if p == self.w: # 如果 p=w,将v→w的流量增加x 28 self.flow += x 29 else: # 否则将v→w的流量减少x 30 self.flow -= x 31 32 def __str__(self): 33 return str(self.v) + '→' + str(self.w)
每条边有两个节点,如果一条边是v→w,根据传入的顶点不同,residual_cap_to方法既可以表示Cf(v→w)又可以表示Cf(w→v)。
由于残存网的两个顶点间可能存在两条边,因此在Network类中添加edges方法用来取得连接某一顶点的所有边,包括该顶点的流出边和流入边。
1 class Network(): 2 ''' 流网络 ''' 3 def __init__(self, V:list, E:list, s:int, t:int): 4 ''' 5 :param V: 顶点集 6 :param E: 边集 7 :param s: 原点 8 :param t: 汇点 9 :return: 10 ''' 11 self.V, self.E, self.s, self.t = V, E, s, t 12 13 def edges_from(self, v): 14 ''' 从v顶点流出的边 ''' 15 return [edge for edge in self.E if edge.v == v] 16 17 def edges_to(self, v): 18 ''' 流入v顶点的边 ''' 19 return [edge for edge in self.E if edge.w == v] 20 21 def edges(self, v): 22 ''' 连接v顶点的所有边 ''' 23 return self.edges_from(v) + self.edges_to(v) 24 25 def flows_from(self, v): 26 '''v顶点的流出量 ''' 27 edges = self.edges_from(v) 28 return sum([e.flow for e in edges]) 29 30 def flows_to(self, v): 31 ''' v顶点的流入量 ''' 32 edges = self.edges_to(v) 33 return sum([e.flow for e in edges]) 34 35 def check(self): 36 ''' 源点的流出是否等于汇点的流入 ''' 37 return self.flows_from(self.s) == self.flows_to(self.t) 38 39 def display(self): 40 if self.check() is False: 41 print('该网络不符合守恒定律') 42 return 43 print('%-10s%-8s%-8s' % ('边', '容量', '流')) 44 for e in self.E: 45 print('%-10s%-10d%-8s' % 46 (e, e.cap,e.flow if e.flow < e.cap else str(e.flow) + '*'))
接下来通过FordFulkerson类计算网络中的最大流:
1 class FordFulkerson(): 2 def __init__(self, G:Network): 3 self.G = G 4 self.max_flow = 0 # 最大流 5 6 class Node: 7 ''' 用于记录路径的轨迹 ''' 8 def __init__(self, w, e:Edge, parent): 9 ''' 10 :param w: 顶点 11 :param e: 从上一顶点流入w的边 12 :param parent: 上一顶点 13 ''' 14 self.w, self.e, self.parent = w, e, parent 15 16 def get_augment_path(self): 17 ''' 获取网络中的一条增广路径 ''' 18 path = None 19 visited = set() # 被访问过的顶点 20 visited.add(self.G.s) 21 q = Queue() 22 q.put(self.Node(self.G.s, None, -1)) 23 while not q.empty(): 24 node_v = q.get() 25 v = node_v.w 26 for e in self.G.edges(v): # 遍历连接v的所有边 27 w = e.other_node(v) # 边的另一顶点,e的指向是v→w 28 # v→w有剩余容量且w没有被访问过 29 if e.residual_cap_to(w) > 0 and w not in visited: 30 visited.add(w) 31 node_w = self.Node(w, e, node_v) 32 q.put(node_w) 33 if w == self.G.t: # 到达了汇点 34 path = node_w 35 break 36 return path 37 38 def start(self): 39 ''' 增广路径最大流算法主体方法 ''' 40 while True: 41 path = self.get_augment_path() # 找到一条增广路径 42 if path is None: 43 break 44 bottle = 10000000 # 增广路径的瓶颈 45 node = path 46 while node.parent != -1: # 计算增广路径上的最小剩余量 47 w, e = node.w, node.e 48 bottle = min(bottle, e.residual_cap_to(w)) 49 node = node.parent 50 node = path 51 while node.parent != -1: # 修改残存网 52 w, e = node.w, node.e 53 e.moddify_flow(w, bottle) 54 node = node.parent 55 self.max_flow += bottle # 扩充最大流 56 57 def display(self): 58 print('最大网络流 = ', self.max_flow) 59 print('%-10s%-8s%-8s' % ('边', '容量', '流')) 60 for e in self.G.E: 61 print('%-10s%-10d%-8s' % 62 (e, e.cap, e.flow if e.flow < e.cap else str(e.flow) + '*'))
get_augment_path和《搜索的策略(3)——觐天宝匣上的拼图》 中的bfs方法类似,用先进先出队列实现广度优先搜索,找到残存网中的一条增广路径,并通过visited记录访问过的节点,以确保路径是一条最简路径,Node用于记录路径中经历的节点,start()实现了主体代码。
下面的代码用于寻找图1的最大流:
1 V = [1, 2, 3, 4, 5, 6] 2 E = [Edge(1, 2, 2), Edge(1, 3, 3), Edge(2, 4, 3), Edge(2, 5, 1), 3 Edge(3, 4, 1), Edge(3, 5, 1), Edge(4, 6, 2), Edge(5, 6, 3)] 4 s, t = 1, 6 5 G = Network(V, E, s, t) 6 ford_fullkerson = FordFulkerson(G) 7 ford_fullkerson.start() 8 ford_fullkerson.display()
运行结果:
下章内容:最小st-剪切,切断敌军的补给线
作者:我是8位的