学习安排(8月27日-8月28日)
1.主要学习视频Week9&期末考试
链接(http://www.xuetangx.com/courses/MITx/6_00_2x/2014_T2/courseware/d39541ec36564a88af34d319a2f16bd7/)
2.参考书第13章动态规划
动态规划是一种非常高效的方法,适用于解决具有重复子问题和最优子结构的问题。
- 如果一个问题的全局最优解可以通过组合局部子问题的最优解求出,那么这个问题就具有最优子结构。我们已经见过一些这样的问题,比如归并排序。归并排序对一个列表进行排序的方式就是先对子列表进行排序,然后再合并子列表的排序结果。
- 如果求出一个问题的最优解时需要对同样的某个问题求解多次,那么这个问题就具有重叠子
问题。
0/1背包问题具有这两个特性,尽管不太明显。我们要先看一个更明显具有最优子结构和重叠子问题的问题。
又见斐波那契数列
之前我们介绍了一个很直观的斐波那契数列的递归实现:
def fib(n):
"""假设n是非负整数
返回第n个斐波那契数"""
if n == 0 or n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
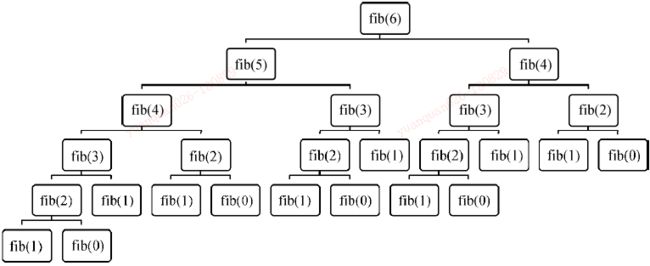
虽然这个递归实现是正确的,但效率太差。复杂度的增长与函数结果的增长成正比,而斐波那契数列的增长速度非常快。举例来说,fib(120)是8 670 007 398 507 948 658 051 921。如果每次递归调用需要1纳秒,那么fib(120)需要250 000年才能结束。fib函数只有寥寥几行代码,很明显问题出在fib函数调用自己的次数上。举个例子,我们看一下fib(6)的调用树:
请注意,我们在一遍又一遍地计算同一个值。例如,fib(3)被调用了3次,而且每一次调用又引发了对fib函数的另外4次调用。很容易就能想到,可以将fib函数的第一次调用结果保存下来,然后在需要的时候直接查找,而不是重新计算。这种方法称为备忘录法,是动态规划的核心思想。
下面给出了一个基于备忘录法的斐波那契函数的具体实现。函数fastFib中有一个参数memo,用来记录已经计算过的函数值,这个参数的默认值是一个空字典。当使用一个大于1的整数n调用fastFib时,fastFib会先在memo中寻找n,如果没有找到(因为这时是第一次使用这个值调用fastFib),就会抛出一个异常。此时,fastFib就使用标准的斐波那契递推公式,并将结果保存在memo中。
def fastFib(n, memo = {}):
"""假设n是非负整数,memo只进行递归调用 返回第n个斐波那契数"""
if n == 0 or n == 1:
return 1
try:
return memo[n]
except KeyError:
result = fastFib(n-1, memo) + fastFib(n-2, memo)
memo[n] = result
return result
动态规划与0/1 背包问题
我们介绍过一种最优化问题,即0/1背包问题。回忆一下,我们介绍了一种复杂度为O(nlog(n))的贪婪算法,但这种算法不能保证找到最优解。除此之外,我们还介绍了一种可以保证找到最优解的暴力算法,但运行时间是指数增长的。动态规划可以提供一种实用的方法,在合理的时间内解决大部分0/1背包问题。作为推导解决方案的第一步,我们先基于穷举法得到一个指数级别的解法。核心思想就是构造一个根二叉树,枚举所有满足重量约束的状态,从而探索可行解空间。
在0/1背包问题的搜索树中,每个节点都使用一个四元组进行标注,这个四元组表示的是这种背包问题的一个局部解。四元组中的四个元素如下:
- 要带走的物品集合;
- 还没有决定是否要带走的物品列表;
- 要带走的物品集合中的物品总价值(这个值只是为了优化算法,因为可以从集合中计算出这个值);
- 背包的剩余空间(这也同样是一种算法优化方式,因为这个值可以通过背包允许的总重量减去当前要带走的物品总重量计算出来)。
这个树是从根节点开始,自顶向下地构建出来的。我们从待定物品中选择出一个,如果背包放得下这个物品,就建立一个节点,反映出选择带走这个物品的后果。按照惯例,我们将这个节点作为左子节点,而用右子节点表示不带走这个物品的后果。以递归方式不断执行这个过程,直到背包被装满或者没有待定物品。因为每条边都表示一个决策(带走或不带走某个物品),所以这种树称为决策树。
如下是一个表示物品集合的表格。
| 名称 | 值 | 重量 |
|---|---|---|
| a | 6 | 3 |
| b | 7 | 3 |
| c | 8 | 2 |
| d | 9 | 5 |
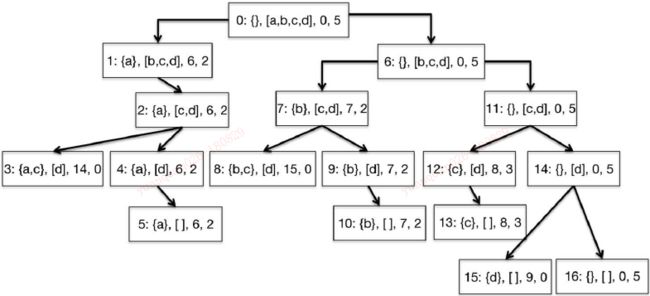
给出一个决策树,在背包能够容纳的最大重量为5的假设之下,可以确定应该带走哪些物品。树的根节点(节点0)有一个标签<{}, [a, b, c, d], 0, 5>,表示没有选择物品,所有物品都处于待定状态,带走的物品总值为0,背包剩余空间还能容纳的重量为5。节点1表示物品a被带走,物品[b, c, d]处于待定状态,带走的物品总值为6,背包还能容纳2的重量。节点1没有左子节点,因为物品b的重量为3,不能放在背包中。
对于每个叶节点,或者第二个元素为空列表(表示没有物品可以考虑是否带走),或者第四个元素为0(表示背包中已经没有剩余空间)。这种深度优先的树搜索使用递归实现如下。
def maxVal(toConsider, avail):
"""假设toConsider是一个物品列表,avail表示重量
返回一个元组表示0/1背包问题的解,包括物品总价值和物品列表"""
if toConsider == [] or avail == 0:
result = (0, ())
elif toConsider[0].getWeight() > avail:
#探索右侧分支
result = maxVal(toConsider[1:], avail)
else:
nextItem = toConsider[0]
#探索左侧分支
withVal, withToTake = maxVal(toConsider[1:],
avail - nextItem.getWeight())
withVal += nextItem.getValue()
#探索右侧分支
withoutVal, withoutToTake = maxVal(toConsider[1:], avail)
#选择更好的分支
if withVal > withoutVal:
result = (withVal, withToTake + (nextItem,))
else:
result = (withoutVal, withoutToTake)
return result
程序中是否还有重叠子问题呢?乍一看似乎没有。在树的每一层,我们考虑的都是不同的可用物品集合,这说明如果确实存在普通的重叠子问题,那么它们一定在树的同一层。实际上,同一层的每个节点的待定物品集合确实是一样的。不过,从图13-4中的标注可以看出,某层的每一个节点的待定物品集合和更高层中节点的待定物品集合是不同的。
考虑一下每个节点需要解决的问题。这个的问题就是,在给定剩余可用重量的情况下,从待定物品集中找到一个最优的物品。决定剩余可用重量的不是带走的具体物品或带走的物品的总价值,而是带走的物品的总重量。所以,举例来说,在决策树图中,节点2和节点7要解决的实际上是同一个问题:在给定剩余可用重量为2的情况下,确定待定物品集合[c, d]中应该带走哪个物品。
下面的代码利用最优子结构和重叠子问题,为0/1背包问题提供了一个动态规划解决方案。通过添加一个附加参数memo,记录已经解决的子问题的解。memo是使用字典实现的,它的键由toConsider的长度和剩余可用重量构成。表达式len(toConsider)是待定物品集合的一种简洁表示,可以这样表示的原因是物品总是从列表toConsider的同一端(前端)被移除。
def fastMaxVal(toConsider, avail, memo = {}):
"""假设toConsider是物品列表,avail表示重量memo进行递归调用
返回一个元组表示0/1背包问题的解,包括物品总价值和物品列表"""
if (len(toConsider), avail) in memo:
result = memo[(len(toConsider), avail)]
elif toConsider == [] or avail == 0:
result = (0, ())
elif toConsider[0].getWeight() > avail:
#探索右侧分支
result = fastMaxVal(toConsider[1:], avail, memo)
else:
nextItem = toConsider[0]
#探索左侧分支
withVal, withToTake =\
fastMaxVal(toConsider[1:],
avail - nextItem.getWeight(), memo)
withVal += nextItem.getValue()
#探索右侧分支
withoutVal, withoutToTake = fastMaxVal(toConsider[1:],
avail, memo)
#选择更好的分支
if withVal > withoutVal:
result = (withVal, withToTake + (nextItem,))
else:
result = (withoutVal, withoutToTake)
memo[(len(toConsider), avail)] = result
return result