ST表--适用多查询O(1)

RMQ问题
给出一个长度为n的区间,m次询问，每次询问l到r这段区间元素的最值，
如果暴力找最值，时间复杂度是O(n)那么总复杂度为O(m*n)
而解决这个问题的方法是ST表和RMQ线段树

ST表类似树状数组，线段树，用于解决RMQ问题(Range Minimum/Maximum Query,即区间最值查询)
的离线算法
与线段树比，预处理复杂度同为O(nlogn)查询时间,ST表为O(1)，线段树为O(nlogn)
对于多查询，建议使用ST表
ST表的主体是一个二维数组ST[i][j],表示需要查询的数组的从下标从i到\(i+2^{j-1}的最值\)

• ST表:一种利用dp求解区间最值得倍增算法
• 定义:st[i][j]表示i到\(2^{j-1}\)这段区间的最值
• 预处理:st[i][0]=a[i],即i到i区间的最大值
  • 状态转移:将st[i][j]分成两段，一段为st[i][j-1]，另一段st[\(i+2^{j-1}\)][j-1]
  • 两段长度均为\(2^{j-1}\)st[i][j]的最大值就是两段的最大值中的最大值
    \(st[i][j]=max(st[i][j-1],st[i+2^{j-1}][j-1])\)
• 查询:需要查询的区间为[i,j]，则需要找到了个覆盖这个闭区间的最小幂区间(这个区间可以重复，因为这个区间是否相交对区间最值没有影响)
  

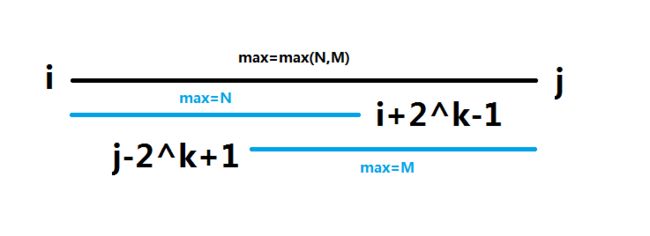
\(很明显ST在查询上比RMQ线段树快很多，而且内存少很多，而树状数组主要是内存比线段树少\)

第一个是ST表，第二个RMQ线段树

ST表

传送门

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn=1e5+5;
const int N=20;//对n进行取对数+1(log(n)+1)
int stmax[maxn][N],stmin[maxn][N];//st[i][j]横着是长度，纵着是元素的大小
int poww[25],logg[maxn];//logg[i]表示小于等于i的2的最大几次放(2^(logg[i])<=i),poww[i]表示2^(i)
int n,m;
void init(){//预处理
    poww[0]=1;
    for(int i=1;i<=N;i++)poww[i]=poww[i-1]<<1;//用于储存2^i
    for(int i=2;i<=n;i++)logg[i]=logg[i>>1]+1;//
    int temp=1;//temp=2^(j-1)
    for(int j=1;j<=logg[n];j++,temp<<=1){
        for(int i=1;i<=n-temp-temp+1;i++){
            stmax[i][j]=max(stmax[i][j-1],stmax[i+temp][j-1]);
            stmin[i][j]=min(stmin[i][j-1],stmin[i+temp][j-1]);
        }
    }
}
inline int query_min(int l,int r){
    int len=r-l+1;
    int k=logg[len];
    return min(stmin[l][k],stmin[r-poww[k]+1][k]);
}
inline int query_max(int l,int r){
    int len=r-l+1;
    int k=logg[len];
    return max(stmax[l][k],stmax[r-poww[k]+1][k]);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        int a;
        scanf("%d",&a);
        stmax[i][0]=stmin[i][0]=a;
    }
    init();
    while(m--){
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",query_max(l,r)-query_min(l,r));

    }
    return 0;
}