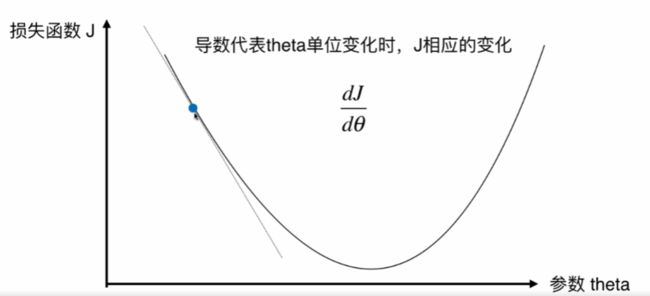
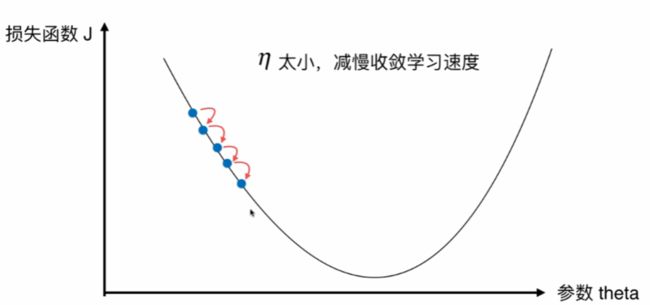
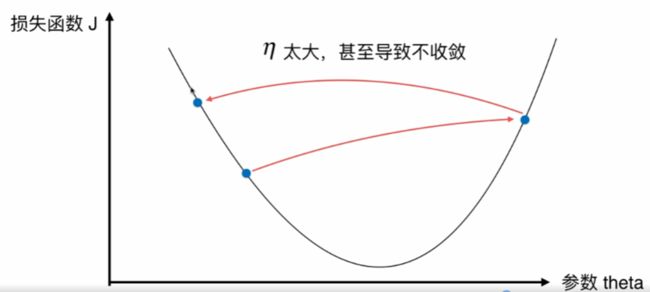
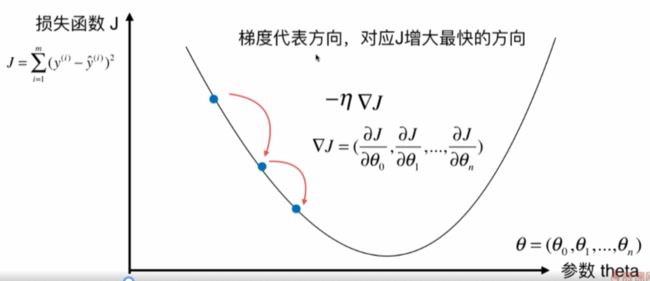
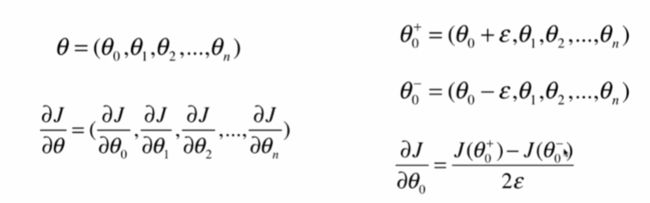什么是梯度下降法
- 不是一个机器学习算法
- 是一种基于搜索的最优化方法
- 作用:最小化一个损失函数
- 梯度上升法:最大化一个效用函数
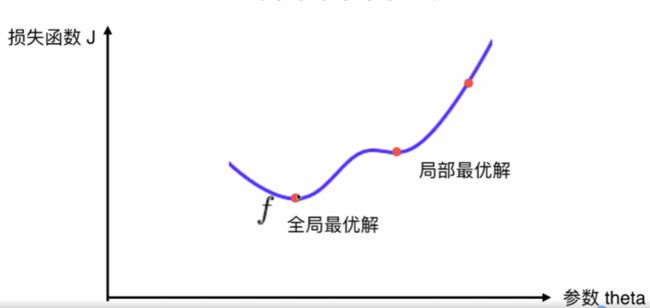
并不是所有函数都有唯一的极值点,解决方案:
- 多次运行,随机化初始点
- 梯度下降发的初始点也是一个超参数
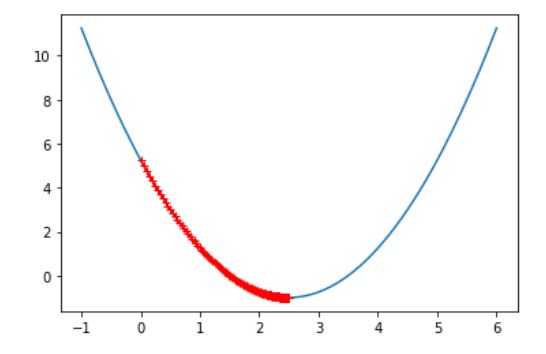
梯度下降法模拟
import numpy as np
import matplotlib.pyplot as plt
plot_x=np.linspace(-1,6,141)
plot_x
plot_y=(plot_x-2.5)**2-1
plt.plot(plot_x,plot_y)
plt.show()
def dJ(theta):#求导
return 2*(theta-2.5)
def J(theta): #损失函数
return (theta-2.5)**2-1
def gradient_descent(initial_theta,eta,n_iters=1e4,eps=1e-8):
theta=initial_theta
theta_history.append(initial_theta)
i_iter=0
while i_iter因为学习率eta过高时,可能会出现无穷大-无穷大的情况,这在python里答案是nan,所以我们要对J()异常处理:
def J(theta):
try:
return (theta-2.5)**2-1.
except:
return float('inf')试一下eta=1.1:
eta=1.1
theta_history=[]
gradient_descent(0,eta)
theta_history[-1]可以发现最后一个数是nan
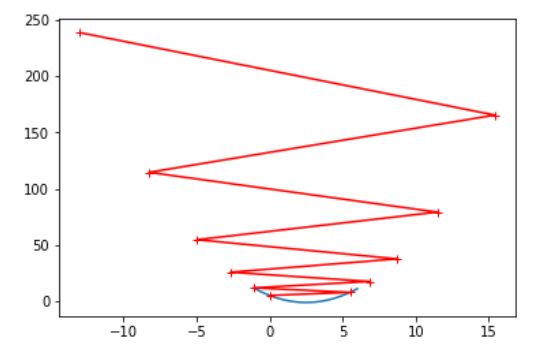
迭代次数取少点,绘制一下图形:
eta=1.1
theta_history=[]
gradient_descent(0,eta,n_iters=10)
plot_theta_history()线性回归中的梯度下降法
import numpy as np
import matplotlib.pyplot as plt
np.random.seed=666
x=2*np.random.random(size=100) #[0,2]的均匀分布
y=x*3.+4.+np.random.normal(size=100) #默认是列向量
X=x.reshape(-1,1)
plt.scatter(x,y)
plt.show()
def J(theta,X_b,y):
try:
return np.sum((y-X_b.dot(theta))**2)/len(X_b)
except:
return float('inf')
def dJ(theta,X_b,y):
res=np.empty(len(theta))
res[0]=np.sum(X_b.dot(theta)-y)
for i in range(1,len(theta)):
res[i]=(X_b.dot(theta)-y).dot(X_b[:,i])#可以看成先求前面的∑部分,最后再和X的第i列点积
return res*2/len(X_b)
def gradient_descent(X_b,y,initial_theta,eta,n_iters=1e4,eps=1e-8):
theta=initial_theta
i_iter=0
while i_iter向量化
上面求到后的式子可以化成矩阵相乘:
图中右下角为最终答案,这是因为Xb是m(样本数)行n(特征值数)列的,所以Xbtheta是m行1列的,即列向量,python中默认是列向量,所以y也是列向量,那么Xb theta - y要转置一下才能变成图中第一行的行向量,最后计算结果还要转置一下才能变成列向量。
添加了梯度下降训练的LinearRegression类:
import numpy as np
from sklearn.metrics import r2_score
class LinearRegression:
def __init__(self):
"""初始化Linear Regression模型"""
self.coef_ = None
self.intercept_ = None
self._theta = None
def fit_normal(self, X_train, y_train):
"""根据训练数据集X_train, y_train训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self, X_predict):
"""给定待预测数据集X_predict,返回表示X_predict的结果向量"""
assert self.intercept_ is not None and self.coef_ is not None, \
"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_), \
"the feature number of X_predict must be equal to X_train"
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
"""根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "LinearRegression()"
import numpy as np
from sklearn import datasets
boston=datasets.load_boston()
X=boston.data
y=boston.target
X=X[y<50.0]
y=y[y<50.0]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666,test_size=0.2)
%run f:\python3玩转机器学习\线性回归\LinearRegression.py
lin_reg1=LinearRegression()
%time lin_reg1.fit_normal(X_train,y_train)
lin_reg1.score(X_test,y_test)
# 梯度下降法
lin_reg2=LinearRegression()
lin_reg2.fit_gd(X_train,y_train)
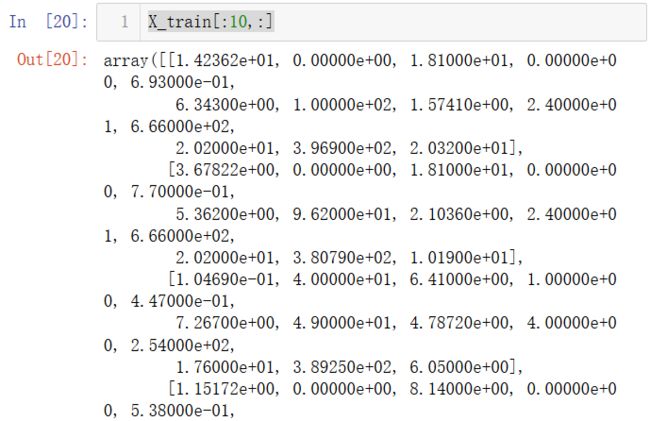
lin_reg2.coef_X_train[:10,:]发现系数都是无穷大,说明学习率太大、训练数据数量级差距太大,导致梯度下降不收敛。
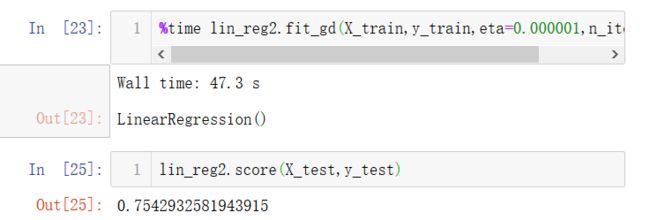
lin_reg2.fit_gd(X_train,y_train,eta=0.000001)
lin_reg2.score(X_test,y_test)#循环次数不够
发现正确率很低,说明可能循环次数不够
%time lin_reg2.fit_gd(X_train,y_train,eta=0.000001,n_iters=1e6)发现准确率提高了,但太耗时了,得另辟蹊径。
归一化
线性回归类中fit_normal采用的是求解正规方程,不涉及搜索的过程,所以不需要数据归一化,时间复杂度O(n^3)。
使用梯度下降法前,最好进行数据归一化。
from sklearn.preprocessing import StandardScaler
standardScaler=StandardScaler()
standardScaler.fit(X_train)
X_train_standard=standardScaler.transform(X_train)
lin_reg3=LinearRegression()
%time lin_reg3.fit_gd(X_train_standard,y_train)可以发现归一化后训练时间优化了很多。
正确率也和正规方程一致了。
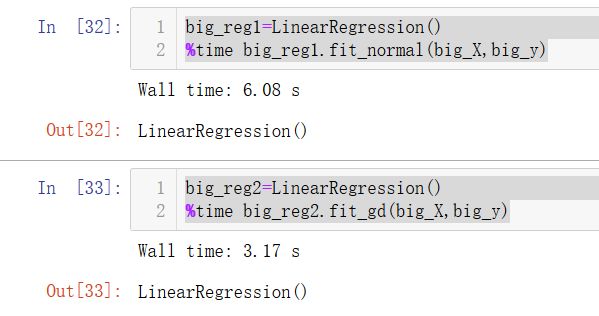
当然,我们可能会发现梯度下降居然比正规方程还慢一点。但是矩阵越大,梯度下降的优势就越强。
m=1000
n=5000
big_X=np.random.normal(size=(m,n)) #正态分布
true_theta=np.random.uniform(0.0,100.0,size=n+1) #n+1个[0,100]的数
big_y=big_X.dot(true_theta[1:])+true_theta[0]+np.random.normal(0.,10.,size=m) #加个均值为0,标准差为10的噪音
big_reg1=LinearRegression()
%time big_reg1.fit_normal(big_X,big_y)
big_reg2=LinearRegression()
%time big_reg2.fit_gd(big_X,big_y)随机梯度下降法
每次随机取一个样本i。
来个例子实战一下看看威力!
import numpy as np
import matplotlib.pyplot as plt
m=500000
x=np.random.normal(size=m) #列向量
X=x.reshape(-1,1)
y=4.*x+3.+np.random.normal(0,3,size=m) #加上噪音
def J(theta,X_b,y):
try:
return np.sum((y-X_b.dot(theta))**2)/len(y)
except:
return float('inf')批量梯度下降:
def dJ(theta,X_b,y):
return X_b.T.dot(X_b.dot(theta)-y)*2/len(y)
def gradient_descent(X_b,y,initial_theta,eta,n_iters=1e4,eps=1e-8):
theta=initial_theta
cur_iter=0
while cur_iter < n_iters:
gradient=dJ(theta,X_b,y)
last_theta=theta
theta=theta-eta*gradient
if(abs(J(theta,X_b,y)-J(last_theta,X_b,y))可以看出和我们刚开始设的斜率和截距是差不多的(4,3)
再看看随机梯度下降法:
def dJ_sgd(theta,X_b_i,y_i):
return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2.
def sgd(X_b,y,initial_theta,n_iters):
t0=1
t1=50
def learning_rate(t):
return t0/(t+t1)
theta=initial_theta
for cur_iter in range(n_iters):
rand_i=np.random.randint(len(X_b))
gradient=dJ_sgd(theta,X_b[rand_i],y[rand_i])
theta=theta-learning_rate(cur_iter)*gradient
return theta
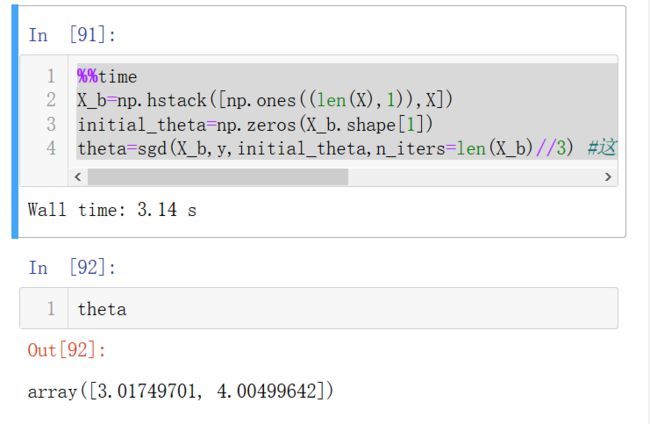
%%time
X_b=np.hstack([np.ones((len(X),1)),X])
initial_theta=np.zeros(X_b.shape[1])
theta=sgd(X_b,y,initial_theta,n_iters=len(X_b)//3) #这里把迭代次数设小一点以看随机梯度下降的威力添加了随机梯度下降训练的LinearRegression类:
import numpy as np
from sklearn.metrics import r2_score
class LinearRegression:
def __init__(self):
"""初始化Linear Regression模型"""
self.coef_ = None
self.intercept_ = None
self._theta = None
def fit_normal(self, X_train, y_train):
"""根据训练数据集X_train, y_train训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_bgd(self, X_train, y_train, eta=0.01, n_iters=1e4):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_sgd(self, X_train, y_train, n_iters=50, t0=5, t1=50):
# 此处的n_iters表示整个样本看几次
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
assert n_iters >= 1
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
def sgd(X_b, y, initial_theta, n_iters=5, t0=5, t1=50):
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b)
#以下代码保证每个样本都被遍历n_iters次
for i_iter in range(n_iters):
indexes = np.random.permutation(m)
X_b_new = X_b[indexes,:]
y_new = y[indexes]
for i in range(m):
gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
theta = theta - learning_rate(i_iter * m + i) * gradient
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self, X_predict):
"""给定待预测数据集X_predict,返回表示X_predict的结果向量"""
assert self.intercept_ is not None and self.coef_ is not None, \
"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_), \
"the feature number of X_predict must be equal to X_train"
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
"""根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "LinearRegression()"再用波士顿房价的例子测试一下:
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston=datasets.load_boston()
X=boston.data
y=boston.target
X=X[y<50.0]
y=y[y<50.0]
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666,test_size=0.2)
from sklearn.preprocessing import StandardScaler
standardScaler=StandardScaler()
standardScaler.fit(X_train)
X_train_standard=standardScaler.transform(X_train)
X_test_standard=standardScaler.transform(X_test)
%run f:\python3玩转机器学习\线性回归\LinearRegression.py
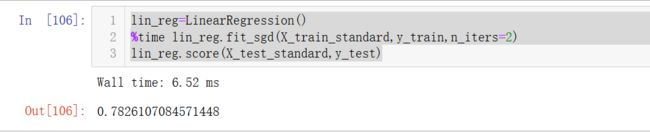
lin_reg=LinearRegression()
%time lin_reg.fit_sgd(X_train_standard,y_train,n_iters=2)
lin_reg.score(X_test_standard,y_test)发现准确率和0.81差不多了:
迭代次数调大:
%time lin_reg.fit_sgd(X_train_standard,y_train,n_iters=100)
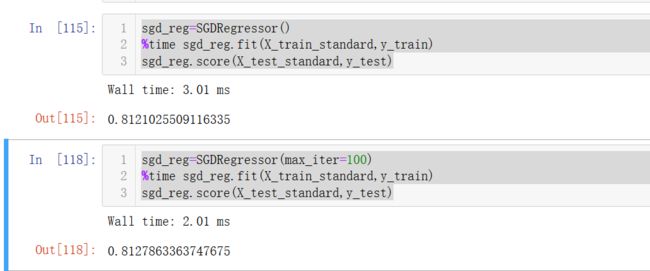
lin_reg.score(X_test_standard,y_test)scikit-learn中的随机梯度下降:
from sklearn.linear_model import SGDRegressor
sgd_reg=SGDRegressor()
%time sgd_reg.fit(X_train_standard,y_train)
sgd_reg.score(X_test_standard,y_test)
sgd_reg=SGDRegressor(max_iter=100)
%time sgd_reg.fit(X_train_standard,y_train)
sgd_reg.score(X_test_standard,y_test)关于梯度的调试
有时候可能梯度求错了但不会报错,这就很坑。
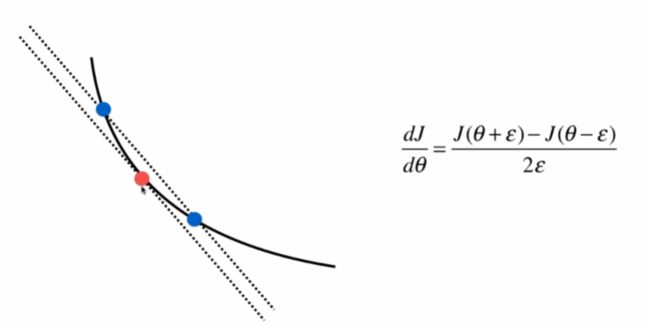
取相邻两个点,这两点的斜率(纵坐标之差/横坐标之差)和切线斜率是差不多的。
对每一个tehta求一遍theta+和theta-,再根据右下角的式子就可以算出这一点切线的斜率,但这样做是非常耗时间的,因此这种方法只适合调试用。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed=666
X=np.random.random(size=(1000,10))
true_theta = np.arange(1,12,dtype=float)
X_b=np.hstack([np.ones((len(X),1)),X])
y=X_b.dot(true_theta)+np.random.normal(size=1000) #加上噪音
def J(theta,X_b,y):
try:
return np.sum((y-X_b.dot(theta))**2)/len(X_b)
except:
return float('inf')
def dJ_math(theta,X_b,y):#数学推导求导
return X_b.T.dot(X_b.dot(theta)-y)*2./len(y)
def dJ_debug(theta,X_b,y,epsilon=0.01):#调试求导
res=np.empty(len(theta))
for i in range(len(theta)):
theta_1=theta.copy()
theta_1[i]+=epsilon
theta_2=theta.copy()
theta_2[i]-=epsilon
res[i]=(J(theta_1,X_b,y)-J(theta_2,X_b,y))/(2*epsilon)
return res
def gradient_descent(dJ,X_b,y,initial_theta,eta,n_iters=1e4,eps=1e-8):#传入求导方法
theta=initial_theta
cur_iter=0
while cur_iter < n_iters:
gradient=dJ(theta,X_b,y)
last_theta=theta
theta=theta-eta*gradient
if(abs(J(theta,X_b,y)-J(last_theta,X_b,y))验证出我们数学推导的求导是正确的。
可以发现调试法求导只用到了J(),所以使用所有的损失函数的,而数学推导求导是根据J()来推导出来的。
有关梯度下降的深入讨论
随机:
- 跳出局部最优解,更容易找到全局最优解
- 更快的运行速度
- 机器学习领域很多算法都要使用随机的特点:随机搜索、随机森林
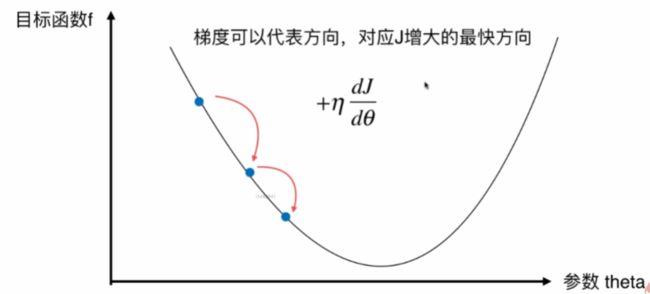
求损失函数J的最大值,可以用梯度上升法: