目录
- 一、图引入
- 二、什么是图(Graph)
- 三、抽象数据类型定义
- 四、常见术语
- 五、怎么在程序中表示一个图
- 六、邻接矩阵
- 6.1 邻接矩阵的优点
- 6.2 邻接矩阵的缺点
- 6.3 邻接矩阵的代码表示
- 6.3.1 c表示
- 6.3.2 Python表示
- 七、邻接表
- 7.1 邻接表的优点
- 7.2 邻接表的缺点
- 7.3 邻接表的代码表示
- 7.2.1 c表示
- 7.3.2 Python表示
更新、更全的《数据结构与算法》的更新网站,更有python、go、人工智能教学等着你:https://www.cnblogs.com/nickchen121/p/11407287.html
一、图引入
相信很多同学都听说过六度空间理论(SixDegress of Separation):只要通过6个人的关系网,你就能够认识全世界所有的人。这个理论和我们接下来要讲的图非常相似。
从上图中,我们可以看出,如果你认识6个人,是很有可能认识其他所有人的。
但是,对于全球的30亿的互联网人来说,你真的可以全部认识吗?大多数同学此刻一定是定神一想,这还用问?你是傻子吗?这一定不可能呀。但是对于这个问题,我们可以用我们未来学习的图的知识解决,啪啪打脸可真不好受,哈哈哈!
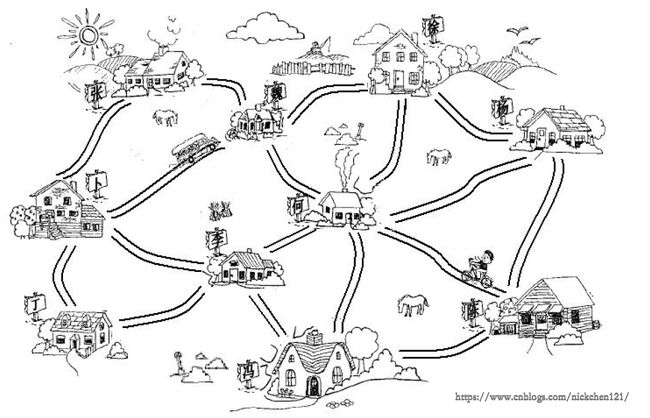
除了上述问题,对于下图,我再来提出两个问题:
- 从陈家庄到张家村,怎么走最快呢?
- 怎么修公路使得村村通的花费最少呢?
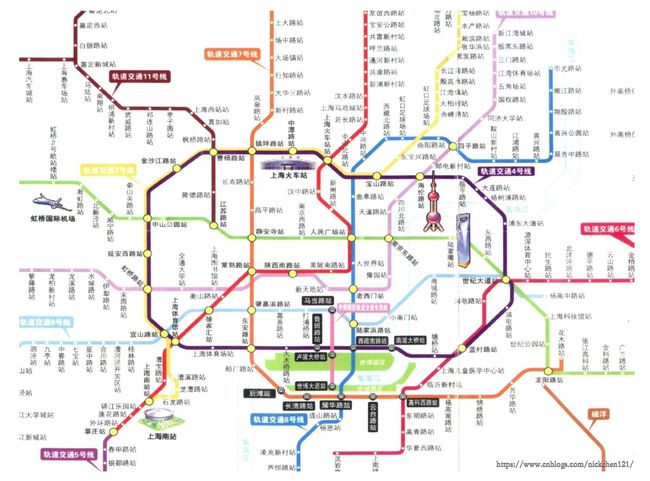
有些同学说了,这还不简单,让我用我的火眼金睛数一数。但是对于下述这张图呢?
算了,我还是街边喊666(溜)吧!!!
二、什么是图(Graph)
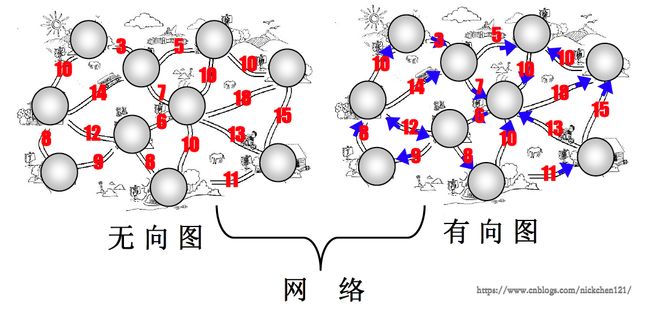
对于上述提出的几个问题,只要你耐下性子和我修习“图法”,相信不久之后,你就不是路边那个只会喊“666”的同志,而是挥手说“同志们好”。那么到底什么是图呢?记住nick心法:图就是下面我讲的这个小东西。废话~,还不如看下图——我(灵魂画师)手绘图:
以前我们学习的链表表示的是一对一的关系;学的树表示一对多的关系;而我们此次的主角,冠勇三军的图却是大有来头,从上图可以看出,图表示的是多对多的关系,通常,它包含如下“小弟”:
- 一组顶点:通常用V(Vertex)表示顶点集合
- 一组边:通常用E(Edge)表示边的集合
三、抽象数据类型定义
我也知道枯燥,但是你逼着自己读一遍都做不到,大江大河等着你逛?
类型名称:图(Graph)
数据对象集:G(V, E),由一个非空的有限顶点集合V和一个有限边集合E组成。
- 操作集:对于任意图\(G\in{Graph}\),以及\(v\in{V},e\in{E}\)
Graph Create():建立并返回空图;Graph InsertVertex(Graph G, Vertex v):将v插入GGraph InsertEdge(Graph G, Edge e):将e插入G;Void DFS(Graph G, Vertex v):从顶点v出发深度优先(别好奇,继续往下看)遍历图G;Void BFS(Graph G, Vertex v):从顶点v出发宽度优先遍历图G;Void ShortestPath(Graph G, Vertex v, int Dist[]):计算图G中顶点v到任意其他顶点的最短距离;Void MST(Graph G):计算图G的最小生成树;- ……,以后都会讲到的,别急,现在不想弄死你,否则你醉生梦死(秃头)走不动了怎么办???
四、常见术语
你随便找一本图论的书,图的常见术语随随便便几十页,为了再次不让你醉生梦死,我就例举出几个,你看着记下就好了:
对,你没有看错,就这几个,还有很多,等以后我慢慢道来……,弄不死你!
五、怎么在程序中表示一个图
理论这东西怎么能符合我大nick的智商,那就来一点实践的吧!
逼逼叨叨一大堆,你倒是讲讲我们怎么在程序中表示一个图呀?
既然你选择了死亡,那我就告诉你吧。在程序中,我们一般有以下两种方式表示图(这并不意味着只有两个,多着呢!),分别为邻接矩阵和邻接表,下面重点戏来了,你个戏精,不是你想要来点实践的吗?
六、邻接矩阵
别听到矩阵就慌了阵脚,有我这个冠勇三军的大nick在,怕啥怕,来吧!
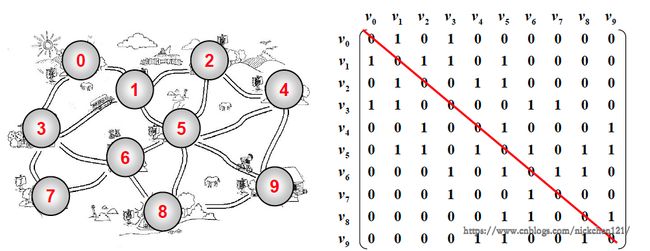
你可以把邻接矩阵看成一个正方形,也可以看成一个二维平面直角坐标轴,也可以混在一起看。我们先来看看它长啥挫样:
不可否认的是,这张图是有点难理解的,但是你要重视接下来我讲的这两句话:
邻接矩阵G[N][N]——N个顶点从0到N-1编号
\[ G[i][j] = \begin{cases} 1\quad\text{若$
不理解,私信我,微信:a1171958281,喷不死你!
对于上图的邻接矩阵,其实存在一个很大的bug,上图的邻接矩阵是沿红线对称的,也就是说,我们是否可以做到如下图所示,只要红色区域的部分呢?这样就可以节省一半空间了,好开心呀!
为了解决存储占用问题,我们可以用一个长度为\(N(N+1)/2\)的1维数组A存储,\(\{G_{00},G_{10},G_{11},\cdots,G_{n-1,0},\cdots,G_{n-1,n-1}\}\),\(G_{ij}\)在数组A中的下标是(一行一行数过去,然后计算它的位置):
\[ (i*(i+1)/2+j) \]
对于边具有权重的网络(不理解就算了),只要把G[i][j]的值定义为边\(
6.1 邻接矩阵的优点
上面逼逼了一大堆邻接矩阵的理论,实在让人痛苦,那么使用邻接矩阵有啥好处呢?好处大大的有,有以下四点好处:
- 直观、简单、好理解,这难道不是优点吗?/偷笑
- 方便检查任意一对顶间是否存在边
- 方便找任一顶点的所有邻接点(有边直接相连的顶点)
- 方便计算任一顶点的度(从该点触发的边数为出度,指向该点的边数为入度)
- 无向图:对应行(或列)非0元素的个数(出度就是入度呀!!!)
- 有向图:对应行非0元素的个数是出度;对应列非0元素的个数是入度
6.2 邻接矩阵的缺点
作为一个一个冠勇三军的大nick,不能总鼓励,也得给点打压!
那么邻接矩阵有什么缺点呢?缺点其实不多,就以下两点:
- 浪费空间——存稀疏图(点很多而便很少,其实就是0很多的意思,有大量无效元素)
- 对稠密图(特别是完全图 )
6.3 邻接矩阵的代码表示
逼逼了一大堆,直接上代码吧!为师毕生功力传给你了,你慢慢参悟,c和python版本我都给你准备好了,但是我推荐你先看完理论再去研究代码。
6.3.1 c表示
/* c语言实现 */
/* 图的邻接矩阵表示法 */
#define MaxVertexNum 100 /* 最大顶点数设为100 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边 */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
DataType Data[MaxVertexNum]; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data[]可以不用出现 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
MGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接矩阵 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; VNv; V++)
for (W=0; WNv; W++)
Graph->G[V][W] = INFINITY;
return Graph;
}
void InsertEdge( MGraph Graph, Edge E )
{
/* 插入边 */
Graph->G[E->V1][E->V2] = E->Weight;
/* 若是无向图,还要插入边 */
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; iNe; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; VNv; V++)
scanf(" %c", &(Graph->Data[V]));
return Graph;
} 6.3.2 Python表示
# python语言实现
# python闭门造车版本,没有一定实力,你就别为难自己了
class Graph_Matrix:
"""
Adjacency Matrix
"""
def __init__(self, vertices=[], matrix=[]):
"""
:param vertices:a dict with vertex id and index of matrix , such as {vertex:index}
:param matrix: a matrix
"""
self.matrix = matrix
self.edges_dict = {} # {(tail, head):weight}
self.edges_array = [] # (tail, head, weight)
self.vertices = vertices
self.num_edges = 0
# if provide adjacency matrix then create the edges list
if len(matrix) > 0:
if len(vertices) != len(matrix):
raise IndexError
self.edges = self.getAllEdges()
self.num_edges = len(self.edges)
# if do not provide a adjacency matrix, but provide the vertices list, build a matrix with 0
elif len(vertices) > 0:
self.matrix = [[0 for col in range(len(vertices))] for row in range(len(vertices))]
self.num_vertices = len(self.matrix)
def isOutRange(self, x):
try:
if x >= self.num_vertices or x <= 0:
raise IndexError
except IndexError:
print("节点下标出界")
def isEmpty(self):
if self.num_vertices == 0:
self.num_vertices = len(self.matrix)
return self.num_vertices == 0
def add_vertex(self, key):
if key not in self.vertices:
self.vertices[key] = len(self.vertices) + 1
# add a vertex mean add a row and a column
# add a column for every row
for i in range(self.getVerticesNumbers()):
self.matrix[i].append(0)
self.num_vertices += 1
nRow = [0] * self.num_vertices
self.matrix.append(nRow)
def getVertex(self, key):
pass
def add_edges_from_list(self, edges_list): # edges_list : [(tail, head, weight),()]
for i in range(len(edges_list)):
self.add_edge(edges_list[i][0], edges_list[i][1], edges_list[i][2], )
def add_edge(self, tail, head, cost=0):
# if self.vertices.index(tail) >= 0:
# self.addVertex(tail)
if tail not in self.vertices:
self.add_vertex(tail)
# if self.vertices.index(head) >= 0:
# self.addVertex(head)
if head not in self.vertices:
self.add_vertex(head)
# for directory matrix
self.matrix[self.vertices.index(tail)][self.vertices.index(head)] = cost
# for non-directory matrix
# self.matrix[self.vertices.index(fromV)][self.vertices.index(toV)] = \
# self.matrix[self.vertices.index(toV)][self.vertices.index(fromV)] = cost
self.edges_dict[(tail, head)] = cost
self.edges_array.append((tail, head, cost))
self.num_edges = len(self.edges_dict)
def getEdges(self, V):
pass
def getVerticesNumbers(self):
if self.num_vertices == 0:
self.num_vertices = len(self.matrix)
return self.num_vertices
def getAllVertices(self):
return self.vertices
def getAllEdges(self):
for i in range(len(self.matrix)):
for j in range(len(self.matrix)):
if 0 < self.matrix[i][j] < float('inf'):
self.edges_dict[self.vertices[i], self.vertices[j]] = self.matrix[i][j]
self.edges_array.append([self.vertices[i], self.vertices[j], self.matrix[i][j]])
return self.edges_array
def __repr__(self):
return str(''.join(str(i) for i in self.matrix))
def to_do_vertex(self, i):
print('vertex: %s' % (self.vertices[i]))
def to_do_edge(self, w, k):
print('edge tail: %s, edge head: %s, weight: %s' % (self.vertices[w], self.vertices[k], str(self.matrix[w][k])))
import networkx as nx
import matplotlib.pyplot as plt
def draw_undircted_graph(my_graph):
G = nx.Graph() # 建立一个空的无向图G
for node in my_graph.vertices:
G.add_node(str(node))
for edge in my_graph.edges:
G.add_edge(str(edge[0]), str(edge[1]))
print("nodes:", G.nodes()) # 输出全部的节点: [1, 2, 3]
print("edges:", G.edges()) # 输出全部的边:[(2, 3)]
print("number of edges:", G.number_of_edges()) # 输出边的数量:1
nx.draw(G, with_labels=True)
plt.savefig("undirected_graph.png")
plt.show()# python语言实现
# python导入模块
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
G = nx.Graph()
Matrix = np.array(
[
[0, 1, 1, 1, 1, 1, 0, 0], # a
[0, 0, 1, 0, 1, 0, 0, 0], # b
[0, 0, 0, 1, 0, 0, 0, 0], # c
[0, 0, 0, 0, 1, 0, 0, 0], # d
[0, 0, 0, 0, 0, 1, 0, 0], # e
[0, 0, 1, 0, 0, 0, 1, 1], # f
[0, 0, 0, 0, 0, 1, 0, 1], # g
[0, 0, 0, 0, 0, 1, 1, 0] # h
]
)
# 建立一个空的无向图
for i in range(len(Matrix)):
for j in range(len(Matrix)):
G.add_edge(i, j)
nx.draw(G)
plt.show()七、邻接表
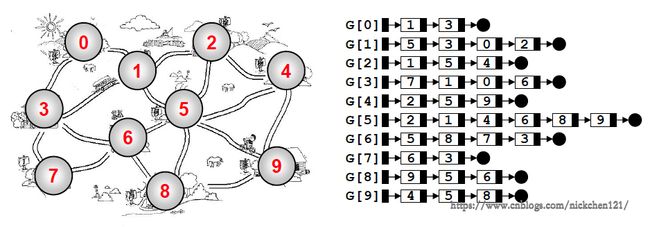
好了,吃完饭了!可以来第二个邻接表了,如下图所示:
对于上图的邻接表,其中G[N]为指针数组,对应矩阵每行一个链表只存非0元素,对于有权重的网络(以后就知道了),结构中增加关于权重的域(多一个权重相关的值)。
但是同志们,一定要注意:图中的顶点之间(邻接矩阵)一定要足够稀疏才合算呀!否则你不就是傻子了吗?
7.1 邻接表的优点
好了,长话短说,邻接表就以下四个优点:
- 方便找任一顶点的所有邻接点
- 节约稀疏图的空间
- 需要N个头指针 + 2E个结点(每个结点至少两个域,头指针5,结点9;也有可能头指针9,结点5)
- 方便计算任一顶点的度
- 无向图:是的
- 有向图:只能计算出度;需要构造逆邻接表(存指向自己的边)来方便计算入度
7.2 邻接表的缺点
就一点,不废话,自己考虑为什么:
- 不方便检查任意一对顶点间是否存在边
7.3 邻接表的代码表示
逼逼了一大堆,直接上代码吧!为师毕生功力传给你了,你慢慢参悟,c和python版本我都给你准备好了,但是我推荐你先看完理论再去研究代码。
7.2.1 c表示
/* c语言实现 */
/* 图的邻接表表示法 */
#define MaxVertexNum 100 /* 最大顶点数设为100 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边 */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
WeightType Weight; /* 边权重 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge;/* 边表头指针 */
DataType Data; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V;
LGraph Graph;
Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接表头指针 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; VNv; V++)
Graph->G[V].FirstEdge = NULL;
return Graph;
}
void InsertEdge( LGraph Graph, Edge E )
{
PtrToAdjVNode NewNode;
/* 插入边 */
/* 为V2建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V2;
NewNode->Weight = E->Weight;
/* 将V2插入V1的表头 */
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
/* 若是无向图,还要插入边 */
/* 为V1建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V1;
NewNode->Weight = E->Weight;
/* 将V1插入V2的表头 */
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = NewNode;
}
LGraph BuildGraph()
{
LGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; iNe; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; VNv; V++)
scanf(" %c", &(Graph->G[V].Data));
return Graph;
} 7.3.2 Python表示
# python语言实现
class Vertex(object):
# 初始化顶点
def __init__(self, key):
self.id = key # 初始化顶点的键
self.connectedTo = {} # 初始化顶点的值
# 添加邻居顶点,参数nbr是邻居顶点的键,默认权重为0
def addNeighbor(self, nbr, weight=0):
self.connectedTo[nbr] = weight
def __str__(self):
return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
# 获取该顶点所有邻居顶点的键
def getConnections(self):
return self.connectedTo.keys()
# 获取顶点的键
def getId(self):
return self.id
# 获取到某邻居顶点的权重
def getWeight(self, nbr):
return self.connectedTo[nbr]
# 自定义图类
class Graph(object):
# 初始化图
def __init__(self):
self.vertList = {} # 初始化邻接表
self.numVertices = 0 # 初始化顶点数
# 添加顶点
def addVertex(self, key):
newVertex = Vertex(key) # 创建顶点
self.vertList[key] = newVertex # 将新顶点添加到邻接表中
self.numVertices = self.numVertices + 1 # 邻接表中顶点数+1
return newVertex
# 获取顶点
def getVertex(self, n):
if n in self.vertList: # 若待查询顶点在邻接表中,则
return self.vertList[n] # 返回该顶点
else:
return None
# 使之可用in方法
def __contains__(self, n):
return n in self.vertList
# 添加边,参数f为起始顶点的键,t为目标顶点的键,cost为权重
def addEdge(self, f, t, cost=0):
if f not in self.vertList: # 起始顶点不在邻接表中,则
self.addVertex(f) # 添加起始顶点
if t not in self.vertList: # 目标顶点不在邻接表中,则
self.addVertex(t) # 添加目标顶点
self.vertList[f].addNeighbor(self.vertList[t], cost) # 在邻接表中添加起始点的目标点及权重
# 获取邻接表中所有顶点的键
def getVertices(self):
return self.vertList.keys()
# 迭代显示邻接表的每个顶点的邻居节点
def __iter__(self):
return iter(self.vertList.values())
if __name__ == '__main__':
g = Graph() # 实例化图类
for i in range(6):
g.addVertex(i) # 给邻接表添加节点
print(g.vertList) # 打印邻接表
g.addEdge(0, 1, 5) # 给邻接表添加边及权重
g.addEdge(0, 5, 2)
g.addEdge(1, 2, 4)
g.addEdge(2, 3, 9)
g.addEdge(3, 4, 7)
g.addEdge(3, 5, 3)
g.addEdge(4, 0, 1)
g.addEdge(5, 4, 8)
g.addEdge(5, 2, 1)
for v in g: # 循环每个顶点
for w in v.getConnections(): # 循环每个顶点的所有邻居节点
print("(%s, %s)" % (v.getId(), w.getId())) # 打印顶点和其邻居节点的键