一致性哈希算法讲解

转自：http://www.evanlin.com/maglev/

前言 （為何想讀這一篇論文)

這一篇論文吸引我注意的原因是，原本 Consistent Hashing 本來的特性就是作為 Load Balancer 之用． 但是 Google 將他們的 Load Balancer (代號: Maglev ) 公布他的實作方式，裡面並且將 Consistent Hashing 做了一些小改版來符合他們的需求．

由於我之前就有學習過 Consistent Hashing ，所以相當好奇 Google 能夠如何地將它更進一步地做提升． 就想要閱讀這一篇論文．

本篇導讀主要內容如下:

• 介紹 Maglev 的特性與其改善的部分

• 回顧 Consistent Hashing

• 介紹 Maglev Hashing

原始論文

Maglev: A Fast and Reliable Software Network Load Balancer

導讀

什麼是 Maglev?

Maglev 是 Google 的軟體 Load Balancer ，不像是一般硬體的 Load Balancer ， 他可以咝性谝话愕 Linux 機器上面． Maglev 在 Google 內部已經咝辛顺^ 六年 ( since 2008 ) ．一台 Maglev 可以處理 10Gbps 的小封包連結．

Maglev 主要的功能與特色

Maglev 作為 Google 內部的高效能軟體 Load Balancer ，他有以下兩個主要功能：

• 新的 Consistent Hashing Algorithm 稱為 Maglev Hashing

• Connection Tracking

回過來講，那什麼是 Consistent Hashing ?

講到 Consistent Hashing 就必須要提到原本 Load Balancer 的咦魇强 Hash Table 的方式來達成，比如說:

• 來源 ip : 1.2.3.4 透過將來源 ip 做 Hashing 過後指向 server1

• 來源 ip : 1.2.3.5 透過將來源 ip 做 Hashing 過後指向 server2

• 來源 ip : 1.2.4.6 透過將來源 ip 做 Hashing 過後指向 server3

依照原先的設計如果 server1 發生了故障，那麼不論如何 1.2.3.4 就無法連接到任何一個伺服器．

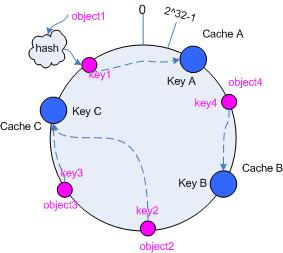
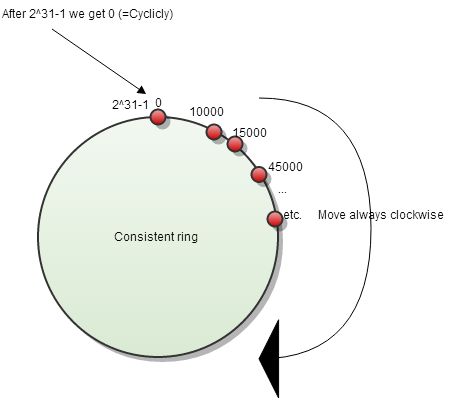
於是 Consistent Hashing 就是在這裡發揮效果． 根據定義 Consistent Hashing 為一個排序的環狀的表格，上面根據 Hashing 的數值來存放不同的節點資訊，並且需要滿足以下兩個條件:

• Minimal Disruption : 這邊指的就是如果有節點被刪除，應該要達到只有該節點影響到的部分要修改而已． 在 Consistent Hashing 裡面透過選取下一個的方式． 透過將索引排序後，直接選取下一個節點作為 Hashing 後的結果節點．簡單的範例如下:

  • 來源 IP 位置 1.2.3.4 ，經過 Hashing 後得到位置 1024 (假設)

  • 到表格 1024 查詢資料，發現 1024 的節點伺服器 server1 已經出現故障．

  • 尋找 1024 最接近的下一個節點 （假設是 1028 ) 並且對應到 server2

  • 分配 server2

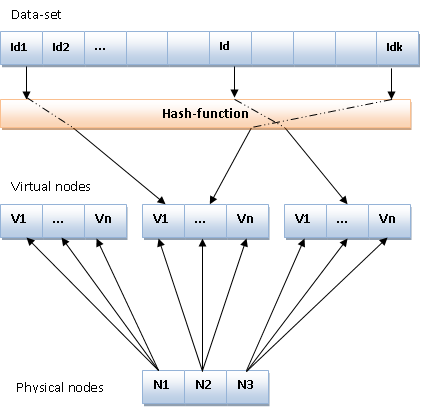
• Load Balancing : 也就是盡可能地讓每個節點都能哂玫剑粫有某些節點有過分哂玫囊蓱]． 在 Consistent Hashing 裡面是使用 Virtual Node ．

  • 簡單的說，也就是在加入節點的時候，會一併複製數個虛擬節點 (通常使用 節點#1, 節點#2 ... 命名方式．

  • 透過多個虛擬節點散佈在各地，讓尋找的時候更容易平均的分配到不同的節點．

對於 Maglev 而言，原本的 Consistent Hashing 有哪些缺點（限制)？

雖然 Consisten Hashing 本身已經解決了許多的問題，但是對於 Google 而言，他們有以下兩個額外的部份需要考量：

• 需要更均勻地分配每隔節點位置： 由於 Google 的每個節點可能都是數百台的機器，由於來源資料龐大，根據舊的演算法可能需要相當大的 lookup table 才能負荷．

• 需要更減少 Disruption : 對於 Google 的需求，演算法需要容忍小量的 disruption ．

關於 Maglev Hashing Algorithm 的介紹

根據以上兩個需要額外考量（應該說是要更加強化）的部分， Google 提出了新的 Consistent Hashing 的演算法，稱為 Maglev Hashing Algorithm

主要概念: 新增 Preference List 概念

Preference List (偏好清單) 會分配給每一個節點，讓每一個節點去填上自己偏好的位址( Permutation )．直到整個表格是填滿的狀態．

效能:

這裡需要注意，如果 M 相當接近 N 的話，整體效能很容易落入最差狀況．

但是如果 M>>N ，比較容易將效能落入平均的狀況．

• 平均狀況: O(MlogM)

• 最差狀況: O(M2)

其中：

• M 是表示 lookup table 的大小．

• N 是表示 節點的個數．

流程:

• 首先 Maglev Hashing 會先把所有的 Preference List 產生出來．

• 透過產生好的 Preference List 開始將節點一個個地加入並且產生出Lookup table

程式碼分析:

計算 “排列表格” Permutation Table

以下先簡單列出 generatePopulation()，主要目的就是建立 permutation table 也就一個排列組合的表格．

//name is the list of backend.func generatePopulation() {
	//如果 []name 是空的就離開
	if len(name) == 0 {
		return
	}

	for i := 0; i < len(name); i++ {
		bData := []byte(name[i])

		//計算 offset 透過 Hash K1
		offset := siphash.Hash(0xdeadbabe, 0, bData) % M
		//計算 skip 透過 Hash K2
		skip := (siphash.Hash(0xdeadbeef, 0, bData) % (M - 1)) + 1

		iRow := make([]uint64, M)
		var j uint64
		for j = 0; j < m.m; j++ {
			//排列組合的表格
			iRow[j] = (offset + uint64(j)*skip) % M
		}

		permutation = append(permutation, iRow)
	}}

由於 M 必須是一個 prime number （如果不給 prime number ，找出的 permutation 就會有重複值) ，舉例 M=7 這個函式就會產生可能是 [3, 2, 5, 6, 0, 4, 1] 或是 [0, 5, 6, 4, 2, 3, 1] ． 這樣的排列表格是為之後使用的．

產生查表表格(Lookup Table)

論文中的 Populate Maglev Hashing lookup table 的 Golang 程式碼．

這邊有兩個表格:

• entry: 代表表格中有沒有走過．架設 lookup table 大小為 7，就得 0 ~ 6 都走過一次． （不然為 -1)．而最後裡面的數值就是節點的索引．

• next: 代表排列表格的下一個位置．如果節點有三個，那麼排列表格就有三組．於是 next 大小也有三個，分別記錄每一個排列表格走到第幾個位置．

範例資料

unc (m *Maglev) populate() {
	if len(m.nodeList) == 0 {
		return
	}

	var i, j uint64
	next := make([]uint64, m.n)
	entry := make([]int64, m.m)
	for j = 0; j < m.m; j++ {
		entry[j] = -1
	}

	var n uint64

	for { //true
		for i = 0; i < m.n; i++ {
			c := m.permutation[i][next[i]]
			for entry[c] >= 0 {
				next[i] = next[i] + 1
				c = m.permutation[i][next[i]]
			}

			entry[c] = int64(i)
			next[i] = next[i] + 1
			n++

			if n == m.m {
				m.lookup = entry
				return
			}
		}

	}

}

以下用簡單的範例資料，希望能夠讓大家更容易了解．

N = 3
M = 5

m.permutation [0] = [4, 3, 2, 1, 0]
m.permutation [1] = [3, 2, 1, 0, 4]
m.permutation [2] = [0, 1, 2, 3, 4]

透過這個範例，建立出 Lookup table 的方式如下：

• 將剛剛建立出的排列表格拿出來

• i=0 ，從第一個排列表格的第一個挑出數值 c1=4 ，那麼 entry[4] = 0 (代表 lookup table 中的 entry[4] 是指向節點 0．

• i=1 ，從第二個排列表格的第一個挑出數值 c2=3 ，那麼 entry[3] = 1

• i=2 ，從第三個排列表個的第一個挑出數值 c3=0 ，那麼 entry[0] = 2

• 重跑 i 迴圈， i=0 ． 從第一個排列表格的第二個( index=1 )挑出數值 c4=3 ，由於 entry[3] 走過了，往後走一個 （next[0] +1) 走到 m.permutation[0][2]=2， 於是 entry[2]=0

• 依此類推，直到所有的 n == M ．此時，也會發現 entry[] 不再存在任何 -1

詳細走法如下圖:

Maglev Hashing 跟 Consistent Hashing 的比較

這部分比較屬於我的心得，建議各位看完論文後再看這段．

• Consistent Hashing

  • 將數值透過 Hash Key 對應到一個 lookup table 的索引 index

  • 如果該 index 沒有節點，往下尋找最接近的節點

  • 將每個節點數值根據 Hashing key 加入 lookup table

  • 製作出 Virtual Node 來達到平衡．

  • 準備工作:

  • 如何查詢:

• Maglev Hashing

  • 數值透過 Hash Key 對應到一個 lookup table 的索引 index

  • 由於準備工作，該 index 必定存在數值

  • 傳回節點資料

  • 需要先建立一個排列表格

  • 並請需要先 透過排列表格做出偏好清單．注意這時候所有 lookup table 每一個索引都有一個節點分配．

  • 準備工作:

  • 如何查詢:

完整程式碼

這邊有我的完整程式碼，大家可以參考一下：

https://github.com/kkdai/maglev