一 什么是线段树?
线段树也叫区间树;线段树是一种二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点;
二 为什么要使用线段树?
在解释这个问题先让我们看一个经典的问题,区间染色;
假设有一面墙,长度为n,每次选择一段墙来进行染色,如下图所示: 首先定义一端长度为n的墙; 然后将4-9这个区间染成黄色; 在将7-15染成绿色; 再将1-5染成蓝色; 再将6-12染成红色;
最后问题来了:
1 问m次操作后我们可以看见多少种颜色?
2 m次操作后,我们可以在[i, j]区间看见多少种颜色?
不管怎样,对于这个问题来说,我们关注的是一个一个的区间,其实对于这个问题只需要两种操作就可以搞定,一个是染色操作(也就是所谓的区间更新),一个是查询操作(区间查询);但是由于我们这个是使用的数组来定义的一面墙,所以查询和更新的操作的时间复杂度都为O(n)级别的,如果我们直接使用数组进行操作系统的系统开销就太大了;因为对于这个问题我们关注点的是一个一个的区间,所以线段树在这里就有了用武之地了;
接下来我们在看一个计算机领域经典的区间查询问题查询一个区间[i, j]的最大值 最小值或者该区间的数字之和;
之前我们的数据结构都是对单个的数据进行操作,显然是不适用于这这样的场景的;这里如果我们将这个问题换成对区间内的数据进行操作会是怎么样的?其实这个问题的本质就是基于区间的统计查询。
放在现在的互联网环境下也有很多这样的问题需要使用到区间查询的操作来完成?
其实这样的问题我们需要注意的是:我们关注的仍然是动态的情况,在这种情况下我们使用线段树会是一个很好的选择;因为动态统计的时候会伴有两个操作一个更新一个查询,如果使用数组来进行操作会极大的增加性能开销;接下来我们来对比一下线段树和数组在对这类问题方面的性能开销
比如:一个电商网站去年一年注册的用户中消费最高的用户是谁?消费最少的用户是谁?
三 线段树概念详解
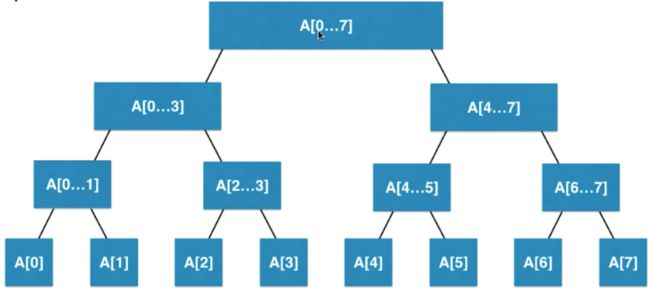
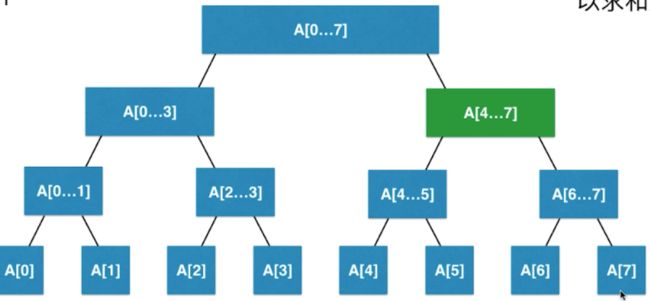
以上的实例我们都可以将数组直接转换成线段树, 这个一个数组,通过以上的实例我们不难发现在线段树中是没有添加和删除操作的,所以转换以后的线段树是这样的 前边也说过线段树是二分搜索树的一种,不同的地方在与线段树每个节点存储的是一个区间,我们以求区间数字之和的问题来进行解析,上图中每一个节点存储一个区间的数据,例如根节点存储的就是整个数组的数据,左右两个子节点存储的就是[0 - 3][4 - 7]这个区间的数据,以此类推;如果我们要操作这些区间数据我们只需要找到这些节点即可,以数组中[4 - 7]这个区间为例: 对于线段树来说有时候我们需要查询的区间需要进行一次合成的操作,比如说在这个实例中我们要查询区间[2 - 5]的数据,就会变成下边的情况:我们需要先找到A[2 - 3]和A[4 - 5]这两个节点,然后对这两个节点在进行合并的操作;
所以在大数量的情况下,如果我们要操作区间数据的话,使用线段树可以很高效的解决我们的问题,而不会像使用数组那样需要先遍历一边所有的元素,这就是线段树的优势所在。
四 线段树的基础表示
1 在之前的例子中我们看到了线段树是一个二分搜索树,但是线段树不一定是一颗满的二叉树,比如说如下图所示: 这是一位,我们的数组是10个元素的数组,根节点保存着10个元素的数据,根节点下边的左右子节点分别保存5个元素,但是左右子节点在往下分的话因为5不能被整除的元素就导致其下边的节点必然会出现元素个数不一致的情况,就像这样的情况: 从图示中可以看出,这个线段树的叶子节点不一定是在最下边一层的,这也表示线段树不一定是满的二叉树同时也不一定是完全二叉树,但是线段树确实一颗平衡二叉树;
平衡二叉树:从根节点开始到叶子节点的深度的差值(最大深度和最小深度)不超过1,从这里我们也可以得出我们的堆也是一颗平衡二叉树,因为完全二叉树本身就是一种平衡二叉树;
- 平衡二叉树的好处就是不会像二分搜索树那样退化成一个链表,在平衡二叉树上进行搜索是非常高效的;
- 我们可以使用数组来表示平衡二叉树,因为我们可以将数组A看成是一个完全二叉树,虽然它最底层的叶子节点有一些是没有的,我们可以将这些节点看成null,这样这个平衡二叉树就会变成完全二叉树,而完全二叉树我们完全可以使用数组来表示;
- 那么问题就来了,如果这个区间有n个元素,我们使用数组表示需要多少个节点? 如图所示,如果区间中有n个元素的话,我们的空间需要2n,因为上边的空间是下边空间之和,但是这有一个最坏的情况,就是我们的数组是奇数的,比如说大小为5这样的情况,那么此时的线段树存储空间就应该是下边这样的 因为区间元素个数为n的话,我们需要2n的空间来进行存储,如果多出一个元素的话我们就需要4n的空间来进行存储,最后我们的线段树模型就应该像下边图示的那样 我们将空的节点全部复制为null,这样就可以让它满足完全二叉树的定义;
注意:在这里我们是浪费了一些存储空间的,由于我们定义的线段树是没有插入操作的也就是说是静态的,那么我们为了性能是完全可以牺牲掉这些空间的;
代码实现线段树基础:
package com.mufeng.segmentTree;
/**
* Created by wb-yxk397023 on 2018/7/8.
*/
public class SegmentTree {
// 线段树使用的数组
private E[] tree;
private E[] data;
public SegmentTree(E[] arr){
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++){
data[i] = arr[i];
}
tree = (E[]) new Object[4 * arr.length];
}
/**
* 获取数组长度
* @return
*/
public int getSize(){
return data.length;
}
/**
* 获取当前索引上的元素
* @param index
* @return
*/
public E get(int index){
if (index < 0 || index >= data.length){
throw new IllegalArgumentException("Index is illega.");
}
return data[index];
}
/**
* 返回完全二叉树的数组表示中,一个索引上元素的左节点索引;
* @param index
* @return
*/
private int leftChild(int index){
return 2 * index + 1;
}
/**
* 返回完全二叉树的数组表示中,一个索引上元素的右节点索引;
* @param index
* @return
*/
private int rightChild(int index){
return 2 * index + 2;
}
}
五 创建线段树
- 首先以求和为例我们先来看一下线段树的模型
在这个图示中,我们的数组长度为10,所以线段树的根节点存储的就是10个元素的和,下边的左右子节点以及各个节点存储的都是相应区间元素的和,如果要创建这样的一个线段树我们就需要使用递归的方法进行创建;
代码实现创建过程
private Merger merger;
public SegmentTree(E[] arr, Merger merger){
this.merger = merger;
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++){
data[i] = arr[i];
}
tree = (E[]) new Object[4 * arr.length];
buildSegmentTree(0, 0, data.length - 1);
}
/**
* 在treeIndex的位置创建表示区间[l....r]的线段树
* @param treeIndex
* @param l
* @param r
*/
private void buildSegmentTree(int treeIndex, int l, int r){
if (l == r){
tree[treeIndex] = data[l];
return;
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r - l) / 2;
buildSegmentTree(leftTreeIndex, l, mid);
buildSegmentTree(rightTreeIndex, mid + 1, r);
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
Merger接口的实现
package com.mufeng.segmentTree;
/**
* Created by wb-yxk397023 on 2018/7/8.
*/
public interface Merger {
E merge(E a, E b);
}
重写toString
/**
* 重写toString方法
* @return
*/
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append('[');
for (int i = 0; i < tree.length; i++){
if (tree[i] != null){
res.append(tree[I]);
}else {
res.append("null");
}
if (i != tree.length - 1){
res.append(", ");
}
}
res.append(']');
return res.toString();
}
测试
package com.mufeng;
import com.mufeng.segmentTree.SegmentTree;
public class Main {
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
SegmentTree segTree = new SegmentTree<>(nums, (a, b) -> a + b);
System.out.println(segTree);
}
}
六 线段树中的区间查询
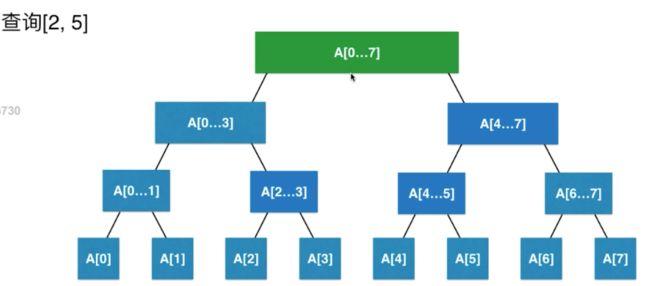
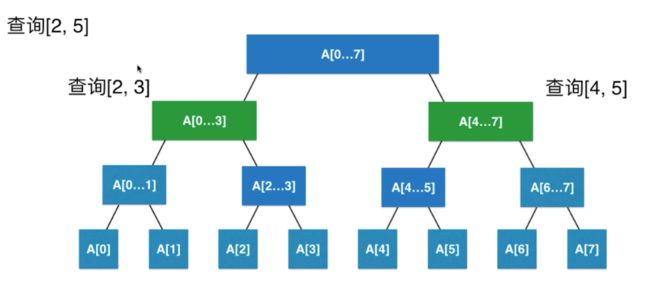
基于递归我们可以很轻松的实现线段树的区间查询操作, 比如说基于这个线段树我们要查询区间为2-5的统计信息; 我们可以先从根节点进行查询; 根据图示我们可以得出要查询[2,5]这个区间的数据就需要查询根节点下左右两个节点的元素,左节点查询[2,3],右节点查询[4,5];由于左右[2,3]和[4,5]这两个节点都有父节点,在这里我们就可以使用递归进行查询;
代码实现线段树区间的查询操作:
/**
* 返回区间[queryL,queryR]的值
* @param queryL
* @param queryR
* @return
*/
public E query(int queryL, int queryR){
if(queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR)
throw new IllegalArgumentException("Index is illegal.");
return query(0, 0, data.length - 1, queryL, queryR);
}
/**
* 线段树区间查询的核心方法
* 在以treeID为根的线段树中[l...r]的范围里,查找[queryL...queryR]的值
* @param treeIndex
* @param l
* @param r
* @param queryL
* @param queryR
* @return
*/
private E query(int treeIndex, int l, int r, int queryL, int queryR){
if (l == queryL && r == queryR){
return tree[treeIndex];
}
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if (queryL >= mid + 1){
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
}else if (queryR <= mid){
return query(leftTreeIndex, l, mid, queryL, queryR);
}
E legtResult = query(leftTreeIndex, l, mid, queryL, mid);
E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
return merger.merge(legtResult, rightResult);
}
测试:
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
SegmentTree segTree = new SegmentTree<>(nums,
(a, b) -> a + b);
System.out.println(segTree);
System.out.println(segTree.query(0, 2));
System.out.println(segTree.query(2, 5));
System.out.println(segTree.query(0, 5));
}
七 线段树中的更新的操作
1⃣️ 代码实现更新操作
/**
* 将index位置上的值更新为e
* @param index
* @param e
*/
public void set(int index, E e){
if (index < 0 || index >= data.length){
throw new IllegalArgumentException("Index is illega.");
}
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
/**
* 在以treeIndex为根的线段树中,更新index的值为e
* @param treeIndex
* @param l
* @param r
* @param index
* @param e
*/
private void set(int treeIndex, int l, int r, int index, E e){
if (l == r){
data[treeIndex] = e;
return;
}
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if (index >= mid + 1){
set(rightTreeIndex, mid + 1, r, index, e);
}else {
set(leftTreeIndex, l, mid, index, e);
}
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}