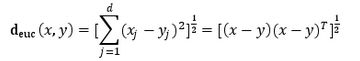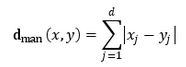keyword
文本分类算法、简单的机器学习算法、基本要素、距离度量、类别判定、k取值、改进策略
摘要
kNN算法是著名的模式识别统计学方法,是最好的文本分类算法之一,在机器学习分类算法中占有相当大的地位,是最简单的机器学习算法之一。
基本信息
外文名:k-Nearest Neighbor(简称kNN)
中文名:k最邻近分类算法
应用:文本分类、模式识别、图像及空间分类
典型:懒惰学习
训练时间开销:0
提出时间:1968年
作者:Cover和Hart提出
关键字:kNN算法、k近邻算法、机器学习、文本分类
工作原理
思想:
官方:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个"邻居"的信息来进行预测。
通俗点说:就是计算一个点与样本空间所有点之间的距离,取出与该点最近的k个点,然后统计这k个点里面所属分类比例最大的(“回归”里面使用平均法),则点A属于该分类。
k邻近法实际上利用训练数据集对特征向量空间进行划分,并作为其分类的“模型”。
三个基本要素:k值的选择、距离度量、分类决策规则
图例说明:
上图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
算法计算步骤
1、算距离: 给定测试对象,计算它与训练集中的每个对象的距离;
2、找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻;
3、做分类:根据这k个近邻归属的主要类别,来对测试对象分类;
类别的判定:
投票法:少数服从多数,近邻中哪个类别的点最多就分为该类。
加权投票法:根据距离的远近,对邻近的投票进行加权,距离越近则权重越大(权重为距离平方的倒数)。
优、缺点
优点:
1、简单,易于理解,易于实现,无需估计参数,无需训练;
2、适合对稀有事件进行分类;
3、特别适合于多分类问题(multi-modal,对象具有多个类别标签), kNN比SVM的表现要好。
缺点:
1、
样本容量较小的类域采用这种算法比较容易产生误分。
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。
2、该方法的另一个不足之处是
计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
3、可理解性差,无法给出像决策树那样的规则。
算法实例
流程:
1、计算距离
2、选择距离最小的k个点
3、通过投票方式,选择点最多的标签。
#-*- coding:utf-8 -*-
import numpy as np
import operator
def createDataset():
#四组二维特征
group = np.array([[5,115],[7,106],[56,11],[66,9]])
#四组对应标签
labels = ('动作片','动作片','爱情片','爱情片')
return group,labels
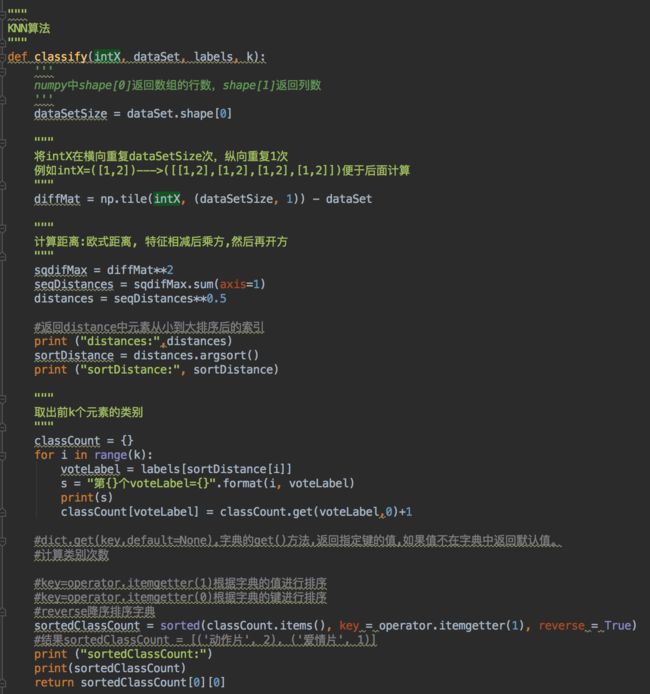
"""
KNN算法
"""
def classify(intX, dataSet, labels, k):
'''
numpy中shape[0]返回数组的行数,shape[1]返回列数
'''
dataSetSize = dataSet.shape[0]
"""
将intX在横向重复dataSetSize次,纵向重复1次
例如intX=([1,2])--->([[1,2],[1,2],[1,2],[1,2]])便于后面计算
"""
diffMat = np.tile(intX, (dataSetSize, 1)) - dataSet
"""
计算距离:欧式距离, 特征相减后乘方,然后再开方
"""
sqdifMax = diffMat**2
seqDistances = sqdifMax.sum(axis=1)
distances = seqDistances**0.5
#返回distance中元素从小到大排序后的索引
print ("distances:",distances)
sortDistance = distances.argsort()
print ("sortDistance:", sortDistance)
"""
取出前k个元素的类别
"""
classCount = {}
for i in range(k):
voteLabel = labels[sortDistance[i]]
s = "第{}个voteLabel={}".format(i, voteLabel)
print(s)
classCount[voteLabel] = classCount.get(voteLabel,0)+1
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)
#结果sortedClassCount = [('动作片', 2), ('爱情片', 1)]
print ("sortedClassCount:")
print(sortedClassCount)
return sortedClassCount[0][0]
if __name__ == '__main__':
group,labels = createDataset()
test = [20,101]
test_class = classify(test,group,labels,3)
print (test_class)
运行结果 :
改进策略
1、对样本属性进行约简。——删除对分类结果影响较小的属性。
2、采用权值的方法(和该样本距离小的邻居权值大)来改进。——依照训练集合中各种分类的样本数量,选取不同数目的最近邻居,来参与分类。
常见问题
1、k值设定
k值选择过小,得到的近邻数过少,会降低分类精度,同时也会放大噪声数据的干扰;而如果k值选择过大,并且待分类样本属于训练集中包含数据数较少的类,那么在选择k个近邻的时候,实际上并不相似的数据亦被包含进来,造成噪声增加而导致分类效果的降低。
如何选取恰当的K值也成为KNN的研究热点。k值通常是采用交叉检验来确定(以k=1为基准)。
经验规则:k一般低于训练样本数的平方根。
投票法没有考虑近邻的距离的远近,距离更近的近邻也许更应该决定最终的分类,所以加权投票法更恰当一些。
3、距离度量方式的选择
高维度对距离衡量的影响:众所周知当变量数越多,欧式距离的区分能力就越差。
变量值域对距离的影响:值域越大的变量常常会在距离计算中占据主导作用,因此应先对变量进行标准化。
4、训练样本的参考原则
学者们对于训练样本的选择进行研究,以达到减少计算的目的,这些算法大致可分为两类。第一类,减少训练集的大小。KNN算法存储的样本数据,这些样本数据包含了大量冗余数据,这些冗余的数据增了存储的开销和计算代价。缩小训练样本的方法有:在原有的样本中删掉一部分与分类相关不大的样本样本,将剩下的样本作为新的训练样本;或在原来的训练样本集中选取一些代表样本作为新的训练样本;或通过聚类,将聚类所产生的中心点作为新的训练样本
在训练集中,有些样本可能是更值得依赖的。可以给不同的样本施加不同的权重,加强依赖样本的权重,降低不可信赖样本的影响。
5、性能问题
kNN是一种懒惰算法,而懒惰的后果:构造模型很简单,但在对测试样本分类地的系统开销大,因为要扫描全部训练样本并计算距离。
已经有一些方法提高计算的效率,例如压缩训练样本量等。
参考文献
机器学习之KNN算法
百度百科-邻近算法
推荐