前言
本文为学习《深度学习入门》一书的学习笔记,详情请阅读原著
五、CNN的实现
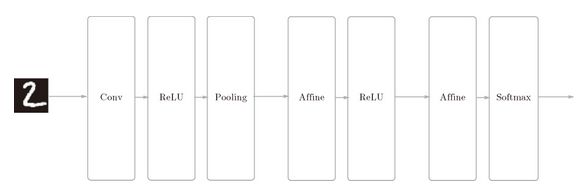
搭建进行手写数字识别的 CNN。这里要实现如图 7-23 所示的 CNN。
图 7-23 简单 CNN 的网络构成
如图 7-23 所示,网络的构成是“Convolution - ReLU - Pooling -Affine - ReLU - Affine - Softmax”,我们将它实现为名为 SimpleConvNet 的类。
首先来看一下 SimpleConvNet 的初始化(__init__),取下面这些参数。
参数
input_dim——输入数据的维度:(通道,高,长)
conv_param——卷积层的超参数(字典)。字典的关键字如下:
filter_num——滤波器的数量
filter_size——滤波器的大小
stride——步幅
pad——填充
hidden_size——隐藏层(全连接)的神经元数量
output_size——输出层(全连接)的神经元数量
weitght_int_std——初始化时权重的标准差
这里,卷积层的超参数通过名为 conv_param 的字典传入。我们设想它会像{'filter_num':30,'filter_size':5, 'pad':0, 'stride':1} 这样,保存必要的超参数值。
SimpleConvNet 的初始化的实现稍长,我们分成 3 部分来说明,首先是初始化的最开始部分。
class SimpleConvNet: def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1}, hidden_size=100, output_size=10, weight_init_std=0.01): filter_num = conv_param['filter_num'] filter_size = conv_param['filter_size'] filter_pad = conv_param['pad'] filter_stride = conv_param['stride'] input_size = input_dim[1] conv_output_size = (input_size - filter_size + 2*filter_pad) / \ filter_stride + 1 pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
这里将由初始化参数传入的卷积层的超参数从字典中取了出来(以方便后面使用),然后,计算卷积层的输出大小。接下来是权重参数的初始化部分。
self.params = {} self.params['W1'] = weight_init_std * \ np.random.randn(filter_num, input_dim[0], filter_size, filter_size) self.params['b1'] = np.zeros(filter_num) self.params['W2'] = weight_init_std * \ np.random.randn(pool_output_size, hidden_size) self.params['b2'] = np.zeros(hidden_size) self.params['W3'] = weight_init_std * \ np.random.randn(hidden_size, output_size) self.params['b3'] = np.zeros(output_size)
学习所需的参数是第 1 层的卷积层和剩余两个全连接层的权重和偏置。将这些参数保存在实例变量的 params 字典中。将第 1 层的卷积层的权重设为关键字W1,偏置设为关键字 b1。同样,分别用关键字 W2、b2 和关键字 W3、b3来保存第 2 个和第 3 个全连接层的权重和偏置。
最后,生成必要的层。
self.layers = OrderedDict() self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad']) self.layers['Relu1'] = Relu() self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2) self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2']) self.layers['Relu2'] = Relu() self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3']) self.last_layer = softmaxwithloss()
从最前面开始按顺序向有序字典(OrderedDict)的 layers 中添加层。只有最后的 SoftmaxWithLoss 层被添加到别的变量 lastLayer 中。
以上就是 SimpleConvNet 的初始化中进行的处理。像这样初始化后,进行推理的 predict 方法和求损失函数值的 loss 方法就可以像下面这样实现。
def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x def loss(self, x, t): y = self.predict(x) return self.lastLayer.forward(y, t)
这里,参数 x 是输入数据,t 是教师标签。用于推理的 predict 方法从头开始依次调用已添加的层,并将结果传递给下一层。在求损失函数的 loss 方法中,除了使用 predict 方法进行的 forward 处理之外,还会继续进行forward 处理,直到到达最后的 SoftmaxWithLoss 层。
接下来是基于误差反向传播法求梯度的代码实现。
def gradient(self, x, t): # forward self.loss(x, t) # backward dout = 1 dout = self.lastLayer.backward(dout) layers = list(self.layers.values()) layers.reverse() for layer in layers: dout = layer.backward(dout) # 设定 grads = {} grads['W1'] = self.layers['Conv1'].dW grads['b1'] = self.layers['Conv1'].db grads['W2'] = self.layers['Affine1'].dW grads['b2'] = self.layers['Affine1'].db grads['W3'] = self.layers['Affine2'].dW grads['b3'] = self.layers['Affine2'].db return grads
参数的梯度通过误差反向传播法(反向传播)求出,通过把正向传播和反向传播组装在一起来完成。因为已经在各层正确实现了正向传播和反向传播的功能,所以这里只需要以合适的顺序调用即可。最后,把各个权重参数的梯度保存到grads 字典中。这就是 SimpleConvNet 的实现。
现在,使用这个 SimpleConvNet 学习 MNIST 数据集。用于学习的代码与 4.5 节中介绍的代码基本相同,因此这里不再罗列(源代码在ch07/train_convnet.py 中)。
如果使用 MNIST 数据集训练 SimpleConvNet,则训练数据的识别率为 99.82%,测试数据的识别率为 98.96%(每次学习的识别精度都会发生一些误差)。测试数据的识别率大约为 99%,就小型网络来说,这是一个非常高的识别率。下一章,我们会通过进一步叠加层来加深网络,实现测试数据的识别率超过 99% 的网络。
如上所述,卷积层和池化层是图像识别中必备的模块。CNN 可以有效读取图像中的某种特性,在手写数字识别中,还可以实现高精度的识别。
六、CNN 的可视化
本节将通过卷积层的可视化,探索 CNN 中到底进行了什么处理。
1、第一层权重的可视化
刚才我们对 MNIST 数据集进行了简单的 CNN 学习。当时,第 1 层的卷积层的权重的形状是 (30, 1, 5, 5),即 30 个大小为 5 × 5、通道为 1 的滤波器。滤波器大小是 5 × 5、通道数是 1,意味着滤波器可以可视化为 1 通道的灰度图像。现在,我们将卷积层(第 1 层)的滤波器显示为图像。这里,我们来比较一下学习前和学习后的权重,结果如图 7-24 所示(源代码在 ch07/visualize_filter.py中)。
图 7-24 中,学习前的滤波器是随机进行初始化的,所以在黑白的浓淡上没有规律可循,但学习后的滤波器变成了有规律的图像。我们发现,通过学习,滤波器被更新成了有规律的滤波器,比如从白到黑渐变的滤波器、含有块状区域(称为 blob)的滤波器等。
图 7-24 学习前和学习后的第 1 层的卷积层的权重:虽然权重的元素是实数,但是在图像的显示上,统一将最小值显示为黑色(0),最大值显示为白色(255)
如果要问图 7-24 中右边的有规律的滤波器在“观察”什么,答案就是它在观察边缘(颜色变化的分界线)和斑块(局部的块状区域)等。比如,左半部分为白色、右半部分为黑色的滤波器的情况下,如图 7-25 所示,会对垂直方向上的边缘有响应。
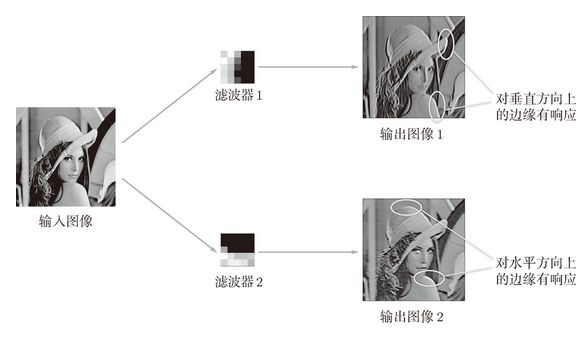
图 7-25 对水平方向上和垂直方向上的边缘有响应的滤波器:输出图像 1 中,垂直方向的边缘上出现白色像素,输出图像 2 中,水平方向的边缘上出现很多白色像素
图 7-25 中显示了选择两个学习完的滤波器对输入图像进行卷积处理时的结果。我们发现“滤波器 1”对垂直方向上的边缘有响应,“滤波器 2”对水平方向上的边缘有响应。
由此可知,卷积层的滤波器会提取边缘或斑块等原始信息。而刚才实现的 CNN 会将这些原始信息传递给后面的层。
2、基于分层结构的信息提取
上面的结果是针对第 1 层的卷积层得出的。第 1 层的卷积层中提取了边缘或斑块等“低级”信息,那么在堆叠了多层的 CNN 中,各层中又会提取什么样的信息呢?根据深度学习的可视化相关的研究 [17][18],随着层次加深,提取的信息(正确地讲,是反映强烈的神经元)也越来越抽象。
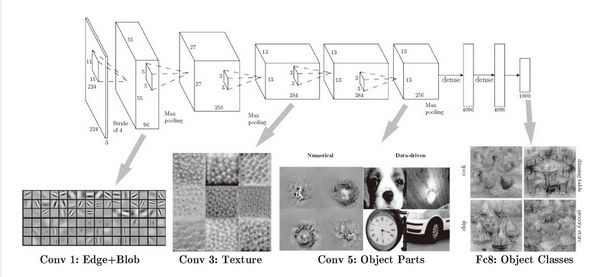
图 7-26 中展示了进行一般物体识别(车或狗等)的 8 层 CNN。这个网络结构的名称是下一节要介绍的 AlexNet。AlexNet 网络结构堆叠了多层卷积层和池化层,最后经过全连接层输出结果。图 7-26 的方块表示的是中间数据,对于这些中间数据,会连续应用卷积运算。
图 7-26 CNN 的卷积层中提取的信息。第 1 层的神经元对边缘或斑块有响应,第 3 层对纹理有响应,第 5 层对物体部件有响应,最后的全连接层对物体的类别(狗或车)有响应
如图 7-26 所示,如果堆叠了多层卷积层,则随着层次加深,提取的信息也愈加复杂、抽象,这是深度学习中很有意思的一个地方。最开始的层对简单的边缘有响应,接下来的层对纹理有响应,再后面的层对更加复杂的物体部件有响应。也就是说,随着层次加深,神经元从简单的形状向“高级”信息变化。换句话说,就像我们理解东西的“含义”一样,响应的对象在逐渐变化。
七、具有代表性的CNN
介绍其中特别重要的两个网络,一个是在 1998 年首次被提出的 CNN 元祖 LeNet[20],另一个是在深度学习受到关注的 2012 年被提出的 AlexNet[21]。
1、LeNet
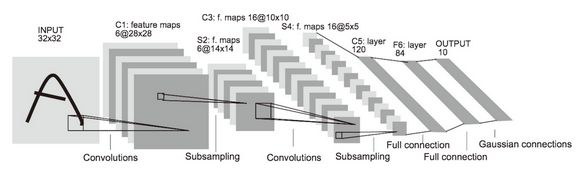
LeNet 在 1998 年被提出,是进行手写数字识别的网络。如图 7-27 所示,它有连续的卷积层和池化层(正确地讲,是只“抽选元素”的子采样层),最后经全连接层输出结果。
图 7-27 LeNet 的网络结构
和“现在的 CNN”相比,LeNet 有几个不同点。第一个不同点在于激活函数。LeNet 中使用 sigmoid 函数,而现在的 CNN 中主要使用 ReLU 函数。此外,原始的 LeNet 中使用子采样(subsampling)缩小中间数据的大小,而现在的 CNN 中 Max 池化是主流。
综上,LeNet 与现在的 CNN 虽然有些许不同,但差别并不是那么大。
2、AlexNet
在 LeNet 问世 20 多年后,AlexNet 被发布出来。AlexNet 是引发深度学习热潮的导火线,不过它的网络结构和 LeNet 基本上没有什么不同,如图 7-28 所示。
图 7-28 AlexNet
AlexNet 叠有多个卷积层和池化层,最后经由全连接层输出结果。虽然结构上 AlexNet 和 LeNet 没有大的不同,但有以下几点差异。
- 激活函数使用 ReLU。
- 使用进行局部正规化的 LRN(Local Response Normalization)层。
- 使用 Dropout(6.4.3 节)。
八、小结
本章所学的内容
- CNN 在此前的全连接层的网络中新增了卷积层和池化层。
- 使用
im2col函数可以简单、高效地实现卷积层和池化层。 - 通过 CNN 的可视化,可知随着层次变深,提取的信息愈加高级。
- LeNet 和 AlexNet 是 CNN 的代表性网络。
- 在深度学习的发展中,大数据和 GPU 做出了很大的贡献。