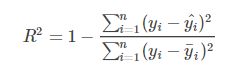- 二分类问题
- 多分类问题
- 连续变量问题
四、连续变量问题(回归)
(1)距离
(2)残差
(3)残差平方和(SSE): 真实值与预测值之间误差的平方和。
(3-1)均方根误差(MSE = mean square error):真实值与预测值之间误差的平方和的均值。(最小二乘)
1 from sklearn.metrics import mean_squared_error
2 y_true = [1,3, -0.3, 2, 7,5]
3 y_pred = [0.8,2.5, 0.0, 2, 8, 5.1]
4 mean_squared_error(y_true, y_pred)
- 均方差越小越好,即最小二乘法。
(4)回归平方和(SSR): 预测值与样本平均值之间误差的平方和。
(5)总偏差平方和(SST): 真实值与样本平均值之间误差的平方和。
经计算推到,SST = SSE + SSR
(5-1)平均绝对误差(MAE = mean absolute error):真实值与样本平均值之间误差的平方和的均值。
1 from sklearn.metrics import mean_squared_error
2 y_true = [1, 3, -0.3, 2, 7, 5]
3 y_pred = [0.8, 2.5, 0.0, 2, 8, 5.1]
4 mean_squared_error(y_true, y_pred)
(6)R2(r2_score):样本的总偏差平方和中,被回归平方和解释的百分比。 R2 = SSR/SST = 1-SSE/SSR (R2值越大,模型效果越好)
1 from sklearn.metrics import r2_score
2 y_true = [1, 3, -0.3, 2, 7, 5]
3 y_pred = [0.8, 2.5, 0.0, 2, 8, 5.1]
4 r2_score(y_true, y_pred)
- R2 越接近1,模型拟合效果越好。
- R2 越接近0,模型拟合效果越差。
- 缺点:数据集越大,R2 越大。因此,不同数据集对同一模型进行测试时,所得的R2 不一定相同。
(7)中值绝对误差(median_absolute_error)
1 from sklearn.metrics import median_absolute_error
2 y_true = [1, 3, -0.3, 2, 7, 5]
3 y_pred = [0.8, 2.5, 0.0, 2, 8, 5.1]
4 median_absolute_error(y_true, y_pred)
总结:
- 以上几个指标全部依赖于数据集,当数据集发生变化时,值也随之发生变化。