词法分析
编译原理笔记第三部分,内容参考:北航软院教师邵兵课堂课件及内容、张莉著《编译原理及编译程序构造》、国防工业出版社的《编译原理——学习指导与典型题解析》、AlvinZH的学习笔记以及个人理解
目前是包含了全部内容的版本,后续会推出精简版和复习知识点版
如有建议或错误错误欢迎在评论中指出或联系我:QQ:847590417
总阅读目录
本章总内容
第一部分:
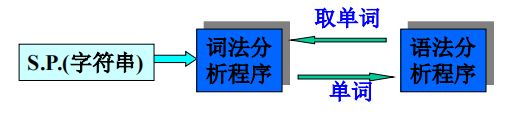
3.1 词法分析程序的功能及实现方案
3.2 单词的种类及词法分析程序的输出形式
3.3 正则文法及状态图
3.3.1 状态图
3.3.2 状态图的使用
3.4 正则表达式与有穷自动机FA
3.4.1 正则表达式
3.4.2 确定的有穷自动机DFA
3.4.3 不确定的有穷自动机NFA
3.4.4 NFA的确定化 子集法
3.4.5 DFA的化简(最小化) 分割法
第二部分:
3.5 有穷自动机、正则文法、正则表达式的转化
3.6 词法分析程序的设计与实现
3.7 词法分析程序的自动生成器LEX
题目讲解
本章总内容
重点:词法分析介绍、词法分析单词种类划分、正则文法、状态图、正则表达式、自动机、自动机的转化、表达式文法和自动机的转化、词法分析程序的设计实现,词法分析程序自动生成器LEX。
剩下的内容
有穷自动机、正则文法、正则表达式的转化,词法分析程序的设计与实现,词法分析程序的自动生成器LEX,题目详解会在第三章的第二部分进行介绍
3.1 词法分析程序的功能及实现方案
词法分析程序的功能是:
1.扫描源程序字符,按语言的词法规则识别出各类单词符号(Token),并将有关字符组合为单词输出,同时进行词法检查;
2.对数字常数完成数字字符串到(二进制)数值的转换;
3.删去空格、换行、制表等字符和注释。(例如ascii码中的9,10,13)
通过词法分析后便可将以字符串表示的源程序加工成为以单词表示的源程序。
实现方式基本上有两种:
1.词法分析单独作为一遍,将字符串转化为单词串,然后在下一遍中进行语法分析
2.词法分析程序作为单独的子程序,词法分析程序和语法分析程序互相调用。
3.2 单词的种类及词法分析程序的输出形式
单词的种类
1.保留字
指语言预定义的字符串,他们有固定的意义
2.标识符
用于定义来表示各种名字的字符串
3.常数
包括无符号数、布尔常数、字符串常数
4.分界符或操作符
可分为单字符分界符和双字符分界符(分界符由几个符号组成)
词法分析程序的输出形式,即单词的内部形式,一般是一个二元式(单词类别+单词值)形式的分类是一个技术性的问题,取决于处理上的方便
1.按单词种类分类
在划分大分类后,统一分类下的单词内容由确定的单词值确定
2.保留字和分界符采用一符一类
这样处理起来方便,因为一个类别只含一个单词,对于这个单词,类别编码就代表其自身的值,不必再判断单词值。
3.标识符和常数的单词值可用指示字(指针)来表示,即标识符在符号表中的地址和常数在常数表中的地址。
3.3 正则文法及状态图
很多程序设计语言的单词都可用乔姆斯基3型文法,即正则文法描述,其描述的语言可用有穷(状态)自动机来识别,状态图既是这种状态机的非形式表示,而正则表达式则可以称为是正则文法的化简
3.3.1 状态图
状态图也称状态转化图,是一个有向图。
结点表示状态,用圆圈表示;结点之间用弧连接,弧上的标记表示弧的射出结点状态下可能出现的输出字符。
每个状态图包含有限个状态,其中有一个初始状态(初态)和至少一个终止状态(终态,双圈表示)
绘制左线性文法的状态图(状态图只能用于左线性文法,这是和后面的DFA的明显区别)状态图的绘制没有严格规定(右线性的暂时不做考虑)
1.文法的非终结符号是一个个的结点
2.设一开始状态S(句子)
3.对规则Q::=t(t为终结符),需要一条从S到Q的一条弧,弧上标记为t
4.对Q::=Rt,画一条从R到Q的弧,弧上标记为t
(倒,谁规约于谁,谁指向谁)
5.根据自动机方法,可加上开始状态和终止状态标志,识别符号作终止状态,用双圆圈标识
3.3.2 状态图的使用
状态图构建后便可接受字符串对其进行分析,分析步骤:
1.字符串为初始状态S,从其的最左字符开始重复步骤2,直到遍历完成
2.扫描字符串的下一字符,在当前状态的向外弧中找出标记为该字符的弧,按方向切换状态。如果没有则说明x不是该文法的句子,当到达最后一个字符且下一个状态为Z,则达到了终止状态,x是该文法的合法句子。
状态图分析是自底向上的分析,每一步的句柄都是当前状态要进入的字符,而句柄所要规约的符号就是下一状态的内容。
3.4 正则表达式与有穷自动机FA
3.4.1 正则表达式
正则表达式是和正则文法等价的,均可表示正则语言,不过正则表达式更为简洁。空集合和空字符串属于正则表达式的内容。
正则表达式的三种操作符:连接、选择和重复,假设有两个正则表达式e1和e2,他们表述的语言是L1和L2.则有:
连接:e1e2,他们标识的语言为L1和L2内句子的拼接,前一个是e1的句子,后一个是e2的句子
选择:e1|e2,表示的语言为L1和L2内所有的句子
重复:e1*即表示表达式的0次到若干次的自重复连接,注意不是闭包,而是任一个e1组成的串
此时在描述一些文法时便非常方便了:
<标识符>=字母(字母|数字)*
<数>=(ε|+|-)(数字*.数字 数字*)(.是小数点,分开两个数字是保证小数点后有数字)
定义:正则集合
有字母表Σ,定义在Σ上的正则表达式和正则集合的递归表示如下:
(1)空符号串和空集都是Σ上的正则表达式,他们的正则集合分别为{ε}和空集φ
(2)任何a属于Σ,a是Σ上的正则表达式,则其正则集合为{a}
(3)假定e1和e2都是Σ上的正则表达式,则他们所表示的正则集合分别即为对应的语言L1和L2:e1|e2也是正则表达式,对应的正则集合:L1∪L2;e1e2也是,对应的正则集合:L1L2;e1*是,正则集合为L1*,即L1的闭包。
(4)所有Σ上的正则表达式和正则集合都有1,2,3产生
正则表达式中操作符的优先级:()优先,*最高,连接其次,|最低。注意括号的是否可省略。
正则表达式的相等也是通过判断他们描述的语言是否相等而得出的
正则表达式也满足一些代数规则:
单位正则表达式:εe=eε=e
交换律:e1|e2=e2|e1
结合律:e1|(e2|e3)=(e1|e2)|e3
e1(e2e3)=(e1e2)e3
分配率:e1(e2|e3)=e1e2|e2e3
(e1|e2)e3=e1e2|e2e3
此外:r*=(r|ε)*,r**=r*,(r|s)*=(r*s*)*
关于正则表达式和其他的转换会在后续(第三章第二部分)进行讲解。
如何证明两个表达式等价:证明他们的语言相同即可。
证明例题如下:
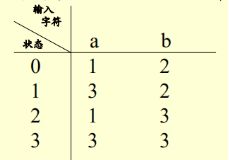
3.4.2 确定的有穷自动机DFA
deterministic finite automaton
即状态图的形式化表述
DFA五元式定义:M=(S,Σ,δ,S0,Z)
S为有穷状态集
Σ为输入字母表
δ(dai er ta)为状态转换函数:
(S×∑ → S的映射)
δ(s,a) = s’ s,s’∈S,a∈Σs’是s的后继状态
s0为初始状态,s0∈S(一个元素)
Z为终止状态集。Z是S子集
按顺序就是五个值
状态转移函数可用矩阵表示:
确定的有穷自动机即状态转换函数是单值函数,不接受ε。
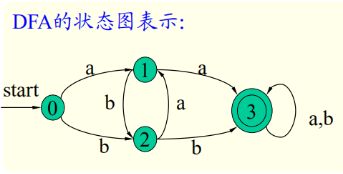
一个DFA也可用一个状态转换图表示:(几个单值函数状态图中的弧的数量就是几个加一,有一个start)
DFA接受的符号串:
对α=a1a2a3...an,α属于Σ*
如果δ(sn-1,an) = sn,sn∈Z,则有δ(s0,α) = sn,即α可被M接受
测试分析时右侧的α可以是一个完整的符号串,然后从左递减到ε,得出的状态如果是S则接受,否则不接受。
即如果存在一条从初始状态到一个终止咋混个台的路径,该路径上所有弧的标记符连接成符号串α,则称α可诶DFA M接受。
对文法M接受的语言为:{α|δ(s0,α)=sn,sn∈Z}
描述语言时正式一点需要用∪符号,而不是或,集合∪即可。
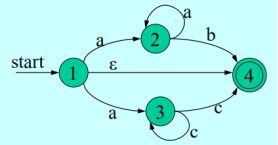
3.4.3 不确定的有穷自动机NFA
NFA的五元式:M’=(S,Σ∪ε,δ,S0,Z)
区别:
输入可为ε
状态转换函数修改为:(S×∑∪{ε} → 2^S的映射,2^S:S的幂集,即S的子集构成的集合)状态转换函数是一个多值函数,且输入允许为ε,即对于某个输入字符存在多个后继状态。
初始状态变为一个集合,不只有一个初始状态。(不是无意大写的)
对文法M’所接受的语言为:L(M′)={α|δ(s0,α)=S’ S’∩Z≠Φ}
α推出的状态集一定需要包含终止状态,除了终止状态也可以有其他状态。
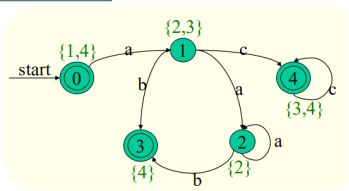
例:
状态图:(弧数同样为单值函数的数量加一,{2,3}相当于两个单值函数)
其接受的语言为:R=aa*b|ac*c|ε
总结:
1.正则表达式和有穷自动机
3型文法所定义的语言都可以用正则表达式描述
用正则表达式描述单词是为了协助生成词法分析程序
有一个正则表达式则对应一个正则集合
若V是正则集合,当且仅当V等于一个M的语言,即一个正则表达式对应一个DFA M。
2.NFA:相比DFA状态转换函数非单值、有ε弧。
3.4.4 NFA的确定化 子集法
利用子集法,根据定义可知,DFA和NFA从功能上是等价的的,即对NFA的M’可以构造出DFA的M,且他们构成的语言相同。
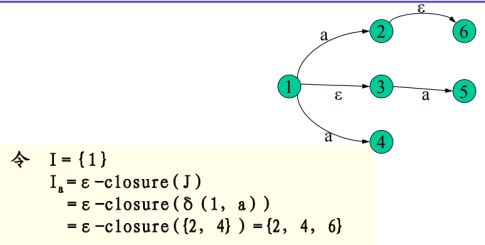
定义:集合I的ε-闭包(ε-closure(I))
令I是一个状态集的子集
1.如果s∈I,则s属于I的ε闭包
2.如果s∈I,则从s出发经过任意条ε弧能够到达的任何状态都属于I的ε闭包。
例:
此时I为{1},则I的ε闭包:{1,3},1一定是,3是经过一个ε弧到达的状态。
定义:令I是NFA M’中状态集的一个自己,a∈Σ
 J是从I中每一个状态出发,经过标记为a的弧(任意长度)能达到的J的集合,Ia是状态子集,即J的ε闭包。
J是从I中每一个状态出发,经过标记为a的弧(任意长度)能达到的J的集合,Ia是状态子集,即J的ε闭包。
例:
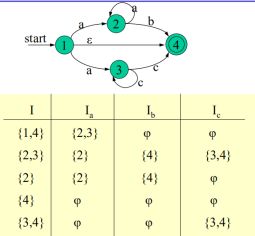
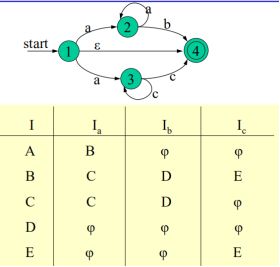
此时便可基于这两个定义进行NFA的确定化:
确定最初的状态子集I(开始状态的ε闭包)
基于I分别对ε外的符号进行求Ia(Ia即Ia,Ib,Ic等等所有鱼符号),求出后如果不为空且不重复,则在下一步对不为空的Ia作为I再次对ε之外的符号求Ia。直到没有新出现的状态子集。
例如:
此时可将所有的状态子集进行变化:
该矩阵既是一个新的状态转换矩阵,对其重新编号既得转化为的DFA M状态转换矩阵:
再画出新的状态图即可:
DFA M的初态:原初始状态1的ε闭包(找出新状态中哪个是1的ε闭包,它既是DFA M初态)
终态:包含终止状态4的状态子集(可有多个,即推导过程中包含状态4的状态子集)
3.4.5 DFA的化简(最小化) 分割法
定理:对任一DFA,都存在一个唯一的状态最少的等价的DFA
这个DFA称为化简的,充要条件为:没有多余状态且它的状态中没有两个是互相等价的。
最小化:即通过消除多余状态和合并等价状态实现
(1)多余状态:从开始状态开始,任何输入串也到达不了的状态(可用状态图辅助寻找)
(2)等价状态,对s和t,他们的等价条件:
1.一致性条件:s和t必须同时为可接受状态或不接受状态(必须同时为终止状态或者不是终止状态)
2.蔓延性条件:对所有输入符号,s和t都转换到等价的状态里(最后会合并)
简易判断:对所有输入符号c,如果Ic(s)=Ic(t),即状态s和t对c具有相同的后继,则他们是等价的。(Ic(s)的符号意义:)
(注:任何有后继的状态和任何无后继的状态一定不等价,不等价即是可区别的)
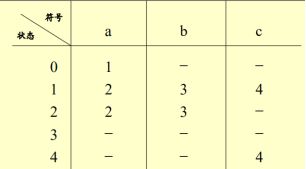
转换方法:分割法,把DFA的状态不断分割为不相关的子集,任何两个不同子集的状态都是可区别的,而同一个子集中的任何状态都等价。
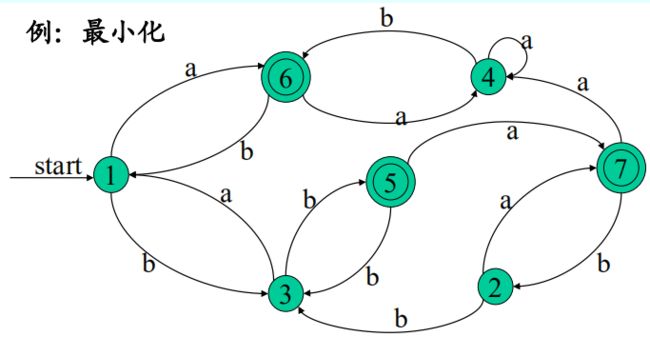
例:
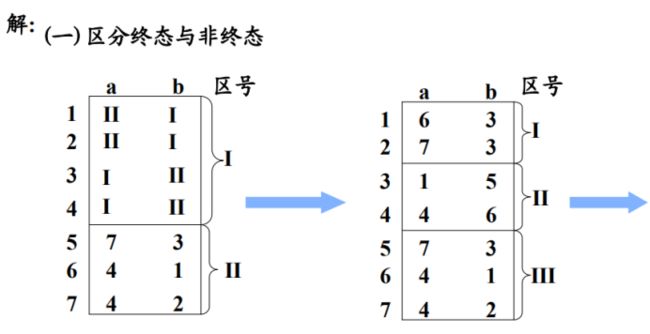
构建:所有状态放左侧,输入字符在上方,转化矩阵依据初态和输入构建,开始状态知道即可,终止状态也记住。
利用一致性条件:将终态和非终态区分开并标号
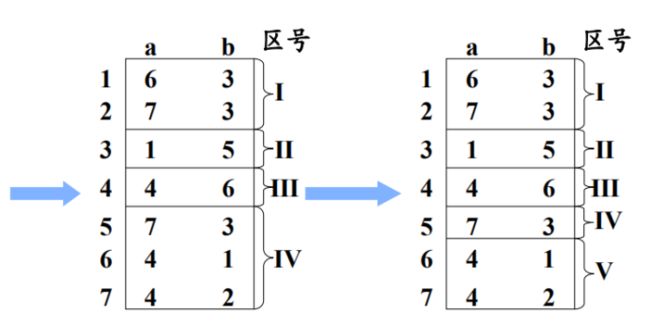
然后不断根据蔓延性条件:判断一个区内的几个状态,当他们遇到符号后进入的区的区号是否相等,将相等的重新划为一个区。
重新划分后再依次判断每个区是否能再次区分开,直到全部无法再划分即可结束,结束即将区号转为状态重新形成DFA即可。