算法设计与分析——最大子段和（分治）

一、问题描述

Description

给定有n个整数(可能为负整数)组成的序列a1,a2,...,an,求该序列连续的子段和的最大值。 如果该子段的所有元素和是负整数时定义其最大子段和为0。

Input

第一行有一个正整数n(n<1000)，后面跟n个整数,绝对值都小于10000。直到文件结束。

Output

输出它的最大子段和。

Sample Input

6 -2 11 -4 13 -5 -2

Sample Output

20

解决该问题有很多方法可以通过暴力、动态规划和分治，这里使用分治的方法来解决该题目。

二、分治策略

 

 

用分治法求解这个问题 。

在数组的 center = (right-left)/2+left 位置处分开。形成两个子数组。

那么，最大子段和 可能出现在三个位置：

　　　　　　　　　　a.可能出现在 左 子数组 

　　　　　　　　　　b. 可能出现在 右子数组 

　　　　　　　　　　c.可能出现在 过center的 中间某部分 元素 组成的子数组。

下面考虑 三种情况的计算方法：

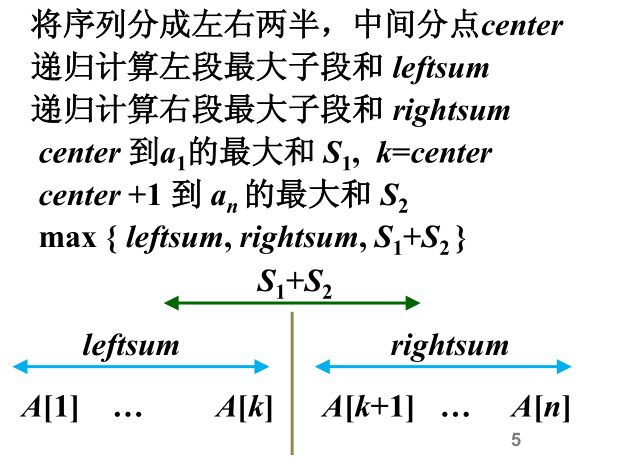
第一种情况： 计算 left 到 center 的最大和，记作 leftSum

第二种情况： 计算从 center+1 到 right的最大和，记作 rightSum

第三种情况： 跨边界的和。 以center为中心分别向两边计算和。

　　　　　　a.从 center出发，每次向左边扩张一步，并且记录当前的值S1，如果当前的和比上次的和大，就更新S1，一直向左扩张到位置 Left。 

　　　　　　b.从 center+1出发，每次扩张一步，计算当前的和 为S2，如果当前的值比上次的和 大，那么，就更新S2的值，一直向右扩张到位置Right。

　　　　　　c.计算过center的连续值的和，S1+S2的值 Sum。 这个就是跨边界的和。

上面三种情况考虑计算完成后，最后一步就是，比较三个值中的最大值，取最大值就可以了。

时间复杂度

我们在（left+right）/2处，把大问题分成了两个部分的小问题。

 

T（N）₁=2T(N） 

T（N）₂=N

 

在跨边界求和的时候，我们需要计算 从center出发的到 left方向的最大和，每次增加一个元素，通过比较，得到最大的和，时间复杂度为O（N），同样， 从center+1 出发的到 right 方向的最大和，每次增加一个元素，通过比较，得到最大的和，时间复杂度 为 O(N) ，所以，时间复杂度为  O(N)。

 

伪代码

源码

import java.util.*;
public class Main
{
    public static int []a =new int[1010];
    public static int maxsum(int l,int r){
        if(l==r){
            return a[l];
        }
        int mid = (l+r)/2;
        int lsum = maxsum(l,mid);//左区间
        int rsum = maxsum(mid+1,r);//右区间
        int sum1=0,sum2=0;
        int lefts=0,rights=0;
        for(int i=mid;i>=l;i--){
            lefts+=a[i];
            if(lefts>sum1){
                sum1=lefts;
            }
        }
        for(int i=mid+1;i<=r;i++){
            rights+=a[i];
            if(rights>sum2){
                sum2=rights;
            }
        }
        int msum=sum1+sum2;
        return Math.max(Math.max(lsum,rsum),msum);
    }
    
    public static void main(String[] args){
        int n;
        int ans;
        Scanner in=new Scanner(System.in);
        while(in.hasNext()){
            n=in.nextInt();
            for(int i=1;i<=n;i++){
                a[i]=in.nextInt();
            }
            ans = maxsum(0,n);
            if(ans<0){
                ans=0;
            }
            System.out.println(ans);
        }
    }
}