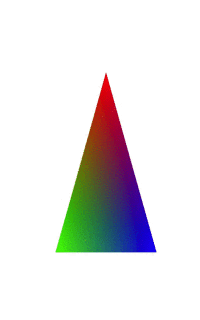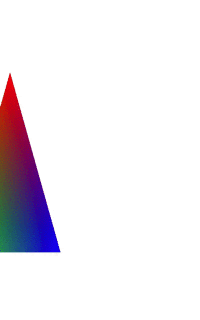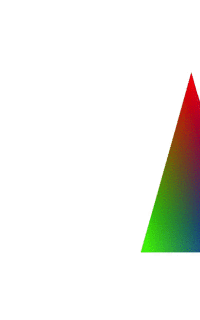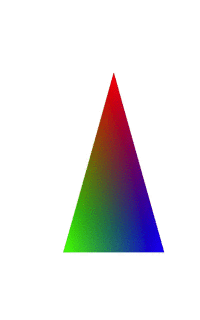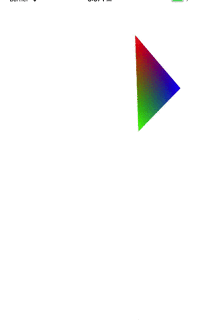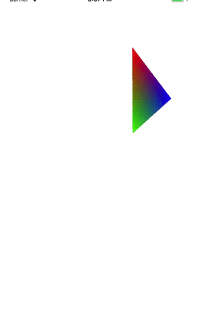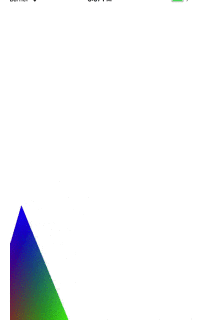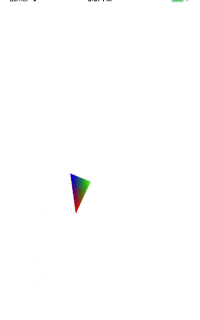从数学上说,变换就是在两个坐标系之间转换顶点坐标。每个坐标系都是相对于其他的参照坐标系定义的。对于OpenGL ES来说,最终的参照坐标系是在一个像素颜色渲染缓存中的像素位置的2D数组。
OpenGL ES中的四种基本变换:平移(translation)、旋转(rotation)。基本变换的联合决定了在一个新的坐标系中的每一个顶点位置是怎么转换为参考坐标系中的一个位置的。四个基本变换足以产生无穷的坐标系。
每个基本变换对应于矩阵的一个简单变化。定义一个与参考坐标系相同的坐标系的矩阵叫做单位矩阵。任意两个矩阵可以在一个联级(又叫矩阵乘法)操作中结合起来以产生一个新矩阵,这个新矩阵包含了两个矩阵的所有变换。实际上,每个基本变换会产生一个简单的矩阵,然后把这个简单的矩阵与当前变换矩阵连接起来以产生一个新的当前矩阵。
定义全局
平移
通过相对于参考坐标系的原点移动新坐标系的原点、平移定义了一个新的坐标系。平移不会影响坐标轴的单位长度,平移不会改变坐标轴相对于参考坐标系的方向。
GLKit提供了GLKMatrix4MakeTranslation(float x,float y,float z)函数,这个函数通过平移一个单位矩阵来返回一个定义了坐标系的新矩阵。x、y、z参数指定了新坐标原点沿着当前参考坐标系的每个轴移动的单位数。
修改代码,看一下GLKit提供的GLKMatrix4MakeTranslation函数实现平移效果。
在顶点着色器中新增了一个uniform mat4 transform。 mat4这个类型前文有提到过,4X4的矩阵。它是Shader内置的类型,支持直接加减乘等操作。使用矩阵会产生更少的运算指令,GPU可以更好的优化运算过程。
attribute vec4 position;
attribute vec4 color;
varying vec4 fColor;
uniform mat4 transform;
void main(void) {
fColor = color;
gl_Position = transform * position;
}
因为我们的数据更新在update里,而赋值绘制在glkView:(GLKView *)view drawInRect:(CGRect)rect中,所以需要定义为全局:
GLKMatrix4 transformMatrix;
// 初始化为单位矩阵,不对图形产生任何变换
transformMatrix = GLKMatrix4Identity;
接下来在应用中创建一个平移变换矩阵:
// 定义一个在值域-1和1之间的局部变量
GLfloat elValue = sinf(changeValue);
// 创建平移变换矩阵,这里只改变了X坐标
GLKMatrix4 translateMatrix =
GLKMatrix4MakeTranslation(elValue, 0.0, 0.0);
把这个变换矩阵赋值到uniform mat4 transform上:
GLuint transformUniformLocation = glGetUniformLocation(program, "transform");
glUniformMatrix4fv(transformUniformLocation, 1, 0, transformMatrix.m);
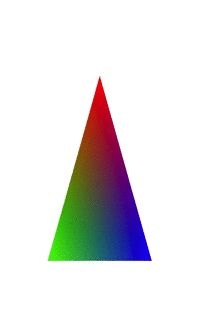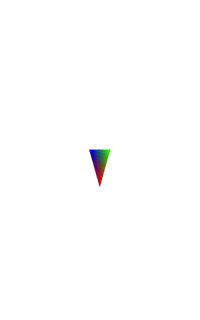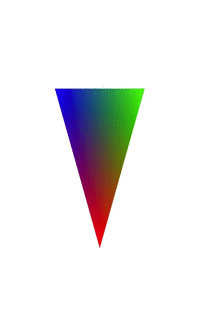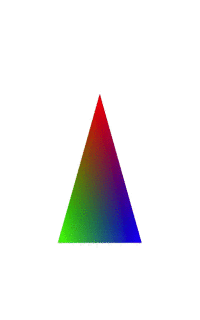
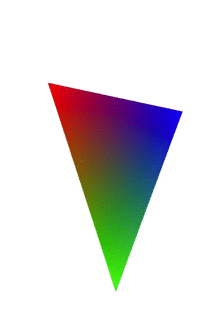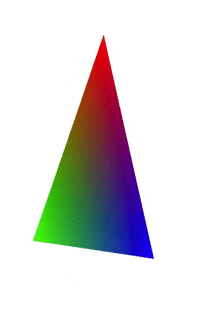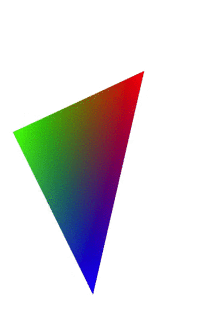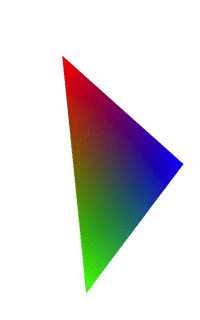
因为我们只是平移了坐标X值,Y和Z值没有变,所以三角形只是沿着X轴平行移动。
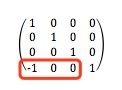
上面的elValue值域为[-1,1],先看一下为-1的时候,我们取其中一个顶点(0,0.5,0)经过(-1,0,0)的平移之后为(-1,0.5,0),我们看一下矩阵计算:如果平移经过(1,0,0)的平移之后就为:(1 0.5 0 1),这就是我们上面看到的三角形的上顶点在屏幕之间移动了。
通过上面的矩阵计算可以发现,平移矩阵就是在一个4x4的变换矩阵中填充第4行前面三个位置:缩放
缩放是通过相对于参考坐标系的坐标轴的单位长度改变新坐标系的坐标轴的单位长度来定义一个新坐标系。缩放坐标系与参考坐标系使用同一个原点。坐标轴的方向通常不会改变。不过,通过一个负值所做的缩放就会翻转坐标轴的方向。
GLKit提供了GLKMatrix4MakeScale(float x,float y,float z)函数,这个函数会通过扩大或者缩小一个单位矩阵的任意坐标轴的单位长度来返回一个定义了坐标系的矩阵。x、y和z参数指定了用来扩大或者缩小每个轴的单位长度的因素。GLKMatrix4Scale(float x,float y,float z)函数通过按指定的因数缩放作为参数传入矩阵来返回一个定义了坐标系的新矩阵。
GLKMatrix4 scaleMatrix = GLKMatrix4MakeScale(elValue, elValue, 1.0);
// 很明显这个矩阵会改变顶点坐标的x、y值
简单分析:elValue为正弦函数的值,所以在-1和1之间,在elValue为1是,不会对原数据有影响,当为-1时,就会翻转坐标轴的方向。所以最终效果就是上图那样,从原图缩小到0,然后负数增大,就是倒过来了。
假定还是点(0.0,0.5,0.0)的x和y值在缩小0.5之后为(0.0,0.25,0.0),看下矩阵计算:旋转
旋转是通过相对于参考坐标系坐标轴的方向旋转新坐标系的坐标轴来定义一个新坐标系。旋转的坐标系会与参考坐标系使用同一个原点。旋转不会影响坐标轴的单位长度,只有坐标轴的方向会发生变化。
GLKit提供了GLKMatrix4MakeRotation(float angleRedians, float x, float y, float z)函数,这个函数通过旋转一个单位矩阵来返回一个定义了坐标系的新矩阵。angleRedians参数指定了要旋转的弧度数。使用GLKMathDegreesToRadians(float degrees)函数可以把角度转换成弧度。x、y和z参数用于指定当前坐标系的哪一个轴作为旋转的轮毂。
例如:GLKMatrix4MakeRotation(GLKMathDegreesToRadians(60.0) , 1.0, 0.0, 0.0)会沿着一个特定的坐标系的X轴旋转60度来产生一个新的坐标系。
相对于平移和缩放,旋转要复杂一些。旋转包含两个重要元素,旋转的角度,绕什么轴旋转。
GLKMatrix4 rotateMatrix = GLKMatrix4MakeRotation(elValue , 0.0, 0.0, 1.0);
// 绕Z轴旋转
除了利用GLKit提供的GLKMatrix4MakeRotation函数直接生成,我们还可以自己定义4x4的旋转矩阵:
// 绕x轴
transformMatrix = GLKMatrix4Make(1.0, 0.0, 0.0, 0.0,
0.0, cos(elValue), -sin(elValue), 0.0,
0.0, sin(elValue), cos(elValue), 0.0,
0.0, 0.0, 0.0, 1.0);
// 绕y轴
transformMatrix = GLKMatrix4Make(cos(elValue),0.0, sin(elValue), 0.0,
0.0, 1.0, 0.0, 0.0,
-sin(elValue),0.0, cos(elValue), 0.0,
0.0, 0.0, 0.0, 1.0);
// 绕z轴
transformMatrix = GLKMatrix4Make(cos(elValue),-sin(elValue), 0.0, 0.0,
sin(elValue), cos(elValue), 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0);
关于旋转矩阵可以参考这篇三维空间中的旋转:旋转矩阵、欧拉角
下面结合三种变换,直接相乘就可以,但是要注意顺序:平移旋转缩放。这样可以保证先缩放,再旋转,最后平移。
// 缩放
GLKMatrix4 scaleMatrix = GLKMatrix4MakeScale(elValue, elValue, 1.0);
// 旋转
GLKMatrix4 rotateMatrix = GLKMatrix4MakeRotation(elValue , 0.0, 0.0, 1.0);
// 平移
GLKMatrix4 translateMatrix = GLKMatrix4MakeTranslation(elValue, elValue, 0.0);
/*
transformMatrix = translateMatrix * rotateMatrix * scaleMatrix
矩阵会按照从右到左的顺序应用到position上。也就是先缩放(scale),再旋转(rotate),最后平移(translate)
如果这个顺序反过来,就完全不同了。从线性代数角度来讲,就是矩阵A乘以矩阵B不等于矩阵B乘以矩阵A。
*/
transformMatrix = GLKMatrix4Multiply(translateMatrix, rotateMatrix);
transformMatrix = GLKMatrix4Multiply(transformMatrix, scaleMatrix);
关于OpenGL ES的三种基本变换就说到这里,其实还有两个重要的投影变换 -- 透视投影和正交投影。就不在本篇继续说了,尽量控制一下篇幅,就在下一篇讲吧!
本例代码:LearningOpenGL ES GitHub