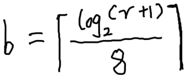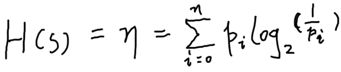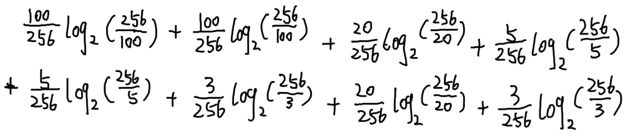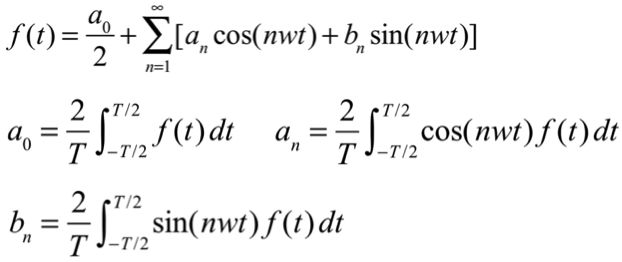1 序
数字媒体技术是迷人的,但是它又充满魔力,吸引了很多开发者投入到该领域中。但是从一名开发者的角度,如何从零开始一步一步成为经验丰富的音视频开发者。如何一步一步建立自己的知识体系,如何从浩瀚如海的数字媒体知识海洋中找到符合当前阶段的重要知识。在这个问题上尽管我现在仍没有明确的答案,但是比刚进入这个领域时更觉前路清晰。
因此,从此篇文章开始,我将站在一个iOS开发者的角度,将搭建属于我的知识体系的心路历程和有相同兴趣的伙伴分享。
2 数字媒体简介
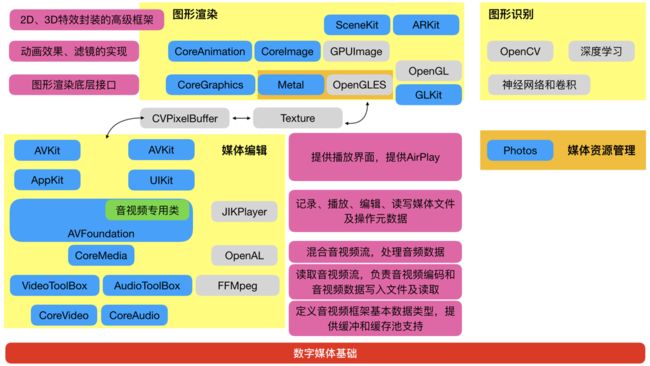
如果对一个领域有野心,那么了解这个领域的基础知识,大的框架是第一步。正如搭建知识树时,总会从枝干开始。要在iOS项目中做出一个游戏的短视频APP,可以所涉及到的知识分为四个部分,媒体编辑、图像渲染、和图形识别、媒体资源管理。它们之间的关系可以表示为下图。
想要掌握上层框架的原理,那么熟悉数字媒体基础中的理论知识则是必不可少的一步。在该部分内容中,我们不会涉及到实践操作,我们不会去编写一段代码从而生成一段视频,也不会去编写一段代码完成一段视频特效。我们更关注的是,当设备的摄像头和麦克风被激活后,数据流是如何被一步一步处理,从而最终形成了一个视频文件。我们会分析其中涉及到的数据采集、量化和编码过程,也会了解这些过程背后的数学知识。
相信很多人和刚入门时的我一样,我们都有过视频开发的经验,尽管从未深入了解数字媒体技术基础中的知识,我们仍坚定的认为我们足够熟悉音视频软件的开发。因此在继续分享之前我们可以问自己如下几个问题:一、使用AVFoundation框架采集视频帧和音频帧时,如何控制视频和音频采样的格式,其中的位深度、颜色空间和采样频率指的都是什么?二、采集到的音频数据如何去除环境噪音?三、图像滤波器是指的什么?它有什么作用?四、音频帧和视频帧是什么?如何确保它们是同步的?五、音频数据和视频数据是如何被编码的?有损编码时损失的是哪部分的数据?
本系列文章将会从数字数据、数字图像、数字音频和数字视频四个方向去介绍数字媒体相关的知识。本篇文章微第一篇,主要讲述数字数据的表示和处理相关知识。
3 模拟数据和数字数据
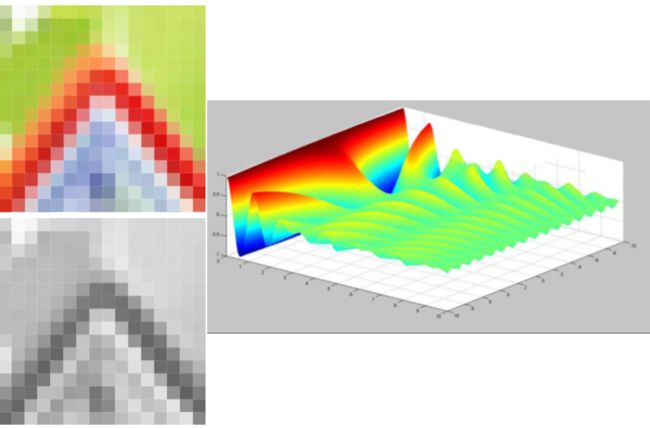
学习数字数据之前了解模拟数据相关知识是必须的,简单的讲模拟数据是连续的数据,而数字数据是在连续数据上的采样,它是离散数据。如下图中的左上角的照片,在自然界中我们所看见的画面任意两点之间我们都可以认为其中有无限个像素。而由上角表示数字数据的照片,我们可以清晰的看见它是由一个一个像素点组成。而数字图像文件保存的就是这些像素点的颜色值。
同样的,左下图表示的音乐是模拟数据,两个音符之间的仍然可以有无穷个渐变的音符组成。而右下角的音频信号表示的是离散的数字音乐,它是由有限个表示声音压强的样本组成。
3.1 模拟音频和数字音频
图像和声音都可以用函数表示,并且可以通过曲线形象的表示出来。声音是一个一维函数,如果将声音看作是一个连续的模拟现象,则可以用函数y=f(x)表示,其中x表示时间,y表示气压振幅。f(x)的基本函数是正弦函数(余弦函数看做是发生相移的正弦函数)。
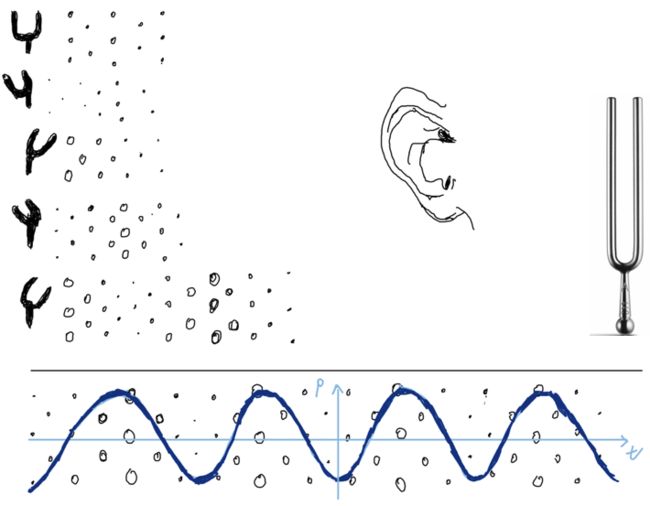
从物理学抽象的角度看,声波是一种机械波,它是通过某种传播介质中质点的运动产生。下图模拟了声波产生的过程。
图的右侧是一个音叉,理论上它只能以固定的频率震动,从而发出频率单一的音波。在音叉静止状态时,空气分子在空间中均匀分布。当音叉向左侧震动时,其右侧进距离的空间范围内,空气分子扩散,该空间内空气压强降低。同样的,当音叉向右侧运动时,其右侧近距离空气压强开始升高。并且上一次压强减低的效应传递到更远处,导致更远处的空气分子向音叉所在的方位运动,从而导致更远处空间内空气压强降级。
当音叉来回震动时,上述物理现象规律发生。导致从音叉附近的空气压强规律变化,如上图下部分描述,其中x轴表示时间,y轴表示空气压强。与此同时在距离音叉不远处的人耳耳膜感受到这种规律的空气压强变换,最终使得我们能听到音叉发出的声音。
使用正弦函数表示一个声波需要将频率f转化为角频率w。他们的换算公式为w = 2πf。如一个频率为440Hz的声波可以使用正弦函数sin(880π)表示。
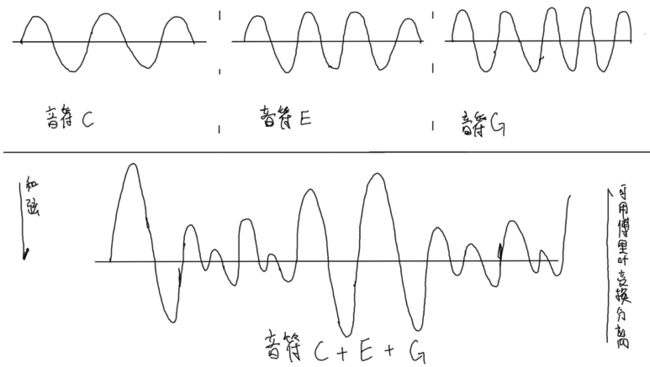
单一频率的音调表示为一个简单的正弦函数,但是自然界中极少的声音只有单一的频率,他们都由多个频率的震动组成。将大量简单的波形组合在一起就可以表示复杂的波形,下入描述了音乐音符C、E、G分别演奏以及他们同时演奏表现和弦时的波形。
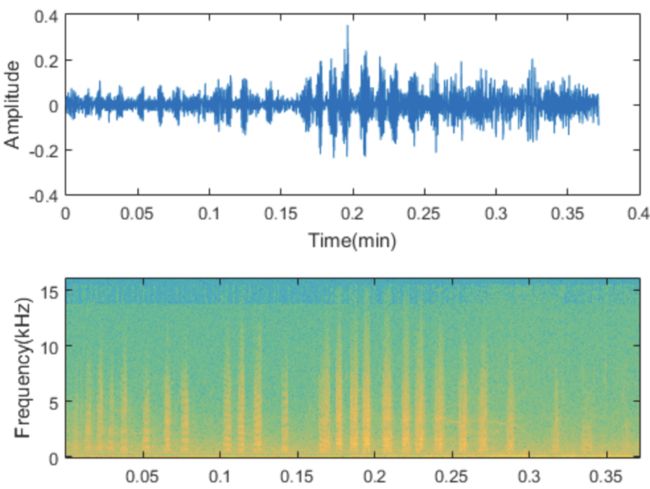
多个简单的音波可以合成复杂的音波,同样的我们也可以将一个复杂的音波分离成多个单一频率的波,这种方法叫傅里叶变换。傅里叶分析表明,任何周期信号都可以分解为无数个正弦波的叠加,简单的正弦波称为复杂波的频率成分。
使用傅里叶变换可以将复杂的声波以数字的形式存储,分析波的频率成分,同时过滤掉不需要的部分。滤波可以用来提高音频的质量或者压缩数字音频文件。
3.2 模拟图像和数字图像
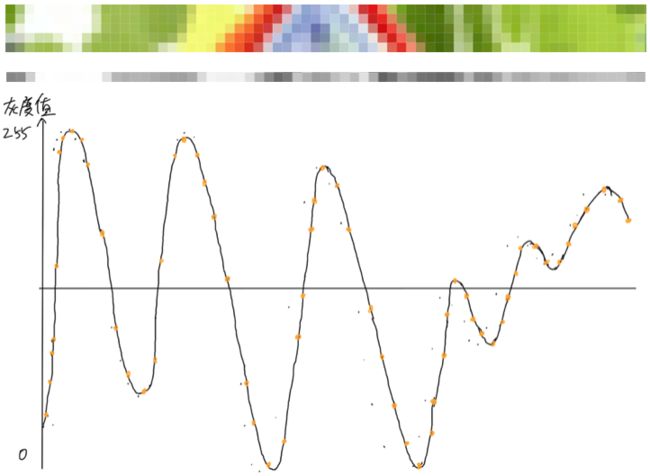
和音频的处理类似,我们也可以将图像抽象为波的形式。如下图所示,顶部的彩色图为衣服图像的一部分。当然这里使用的是数字图像,我们能清晰的在上面看见像素点,当将其延伸到模拟图像并不难,正如前文所描述,模拟图像即我们可以理解为任意两个点之间都有无线个像素点。
中间的灰色条带是其上面彩色图的第一个像素行的灰度图,其中的每一个像素点都可以使用灰度值来表示,其取值范围为0-255,对应着黑色-白色。先将每一个像素的灰度值用黄色的点在下面的坐标系中标出,再由数字图像推广至模拟图像,即图像的每行和每列有无线多个点。因此将黄色的点使用曲线连接,形成了一个复杂的波形。该波形表示了该行图像的颜色变化规律。
同样的,图像上的每一列也可以使用类似的方法抽象出一个正弦函数,绘制出一个波形图。推而广之,我们可以在图像上同时沿着x轴和y轴方向,取得灰度值并绘制波形。此时可以得到一个二维的波形,它可以表示整张图像的灰度变换规律,如下图所示。
对于彩色图像,我们可以将其分解为红绿蓝三个通道,可以得到三个类似的空间二维波形图。
3.3 采样和失真
将声音和图像看成是波形,强调了数据的连续性,波在时间和空间上平滑变换,在选定的两个点之间存在着无数个点。对于数字媒体而言,首要的任务是使用模数转换的方式将模拟信息转换为离散数据。
模数转换分为两个步骤,采样和量化。采样是使用离散的点来衡量一个联系的现象,对于图像而言,样本需要在空间内均匀分布,对于声音而言,样本点需要在时间上均匀分布。每单位时间或者空间上的样本量称为采样率,或者分辨率。
量化要求每个样本用固定的位表示,称为样本容量,或者称为位深度。位深度限制了每个样本的精确度。
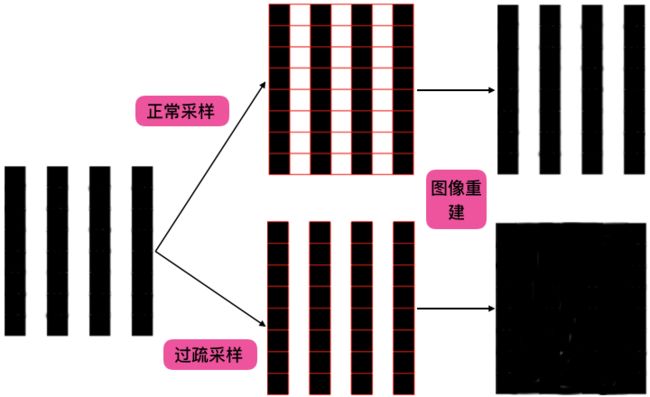
对于下图最左侧的这幅图片,想要沿着水平和垂直方向均匀采样,以数字的方式记录这张图片。在下图中,样本区域指定为矩形块,也称为样本块。对于每个样本块,数码相机会检测其颜色值,并记录为一个像素点。
如果我们对图中上半部门的每个样本块都取样,最后我们能重建出原始的图像。但是如果我们隔行采样,即按照下半部分的方式取样,在图像重建后,我们将得到一张纯黑色的图像,这是一个典型的采样过疏的例子。当我们的采样率没有跟上图像模式的变化率时,会导致图像失真。
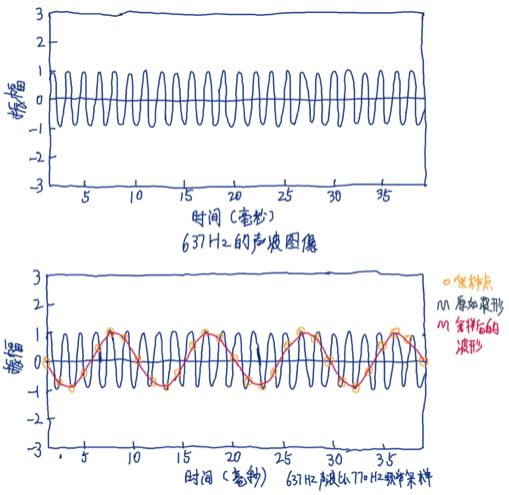
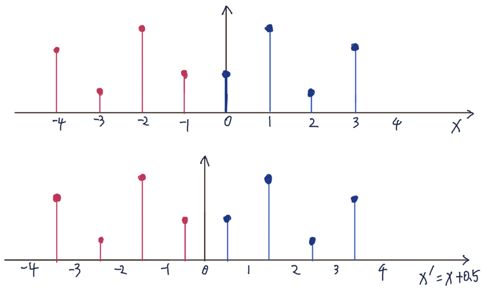
当对声波进行采样的时候我们也会遇到类似的情况。如图中上半部分表示一个频率为637Hz的声音,在图中下半部分,我们使用770Hz(频率在描述采样率时,Hz表示每秒的采样数)的采样频率对该声波采样。其中黄色部分为采样点,此时我们使用这些样本点重建声波的曲线,即图中红色的正弦函数,可以明显发现这不是原来的声音,所以它听上去也与原来的声音不一致。
对于数字图像而言,失真意味着图像不清晰,或者得到的图像和源图像不一致。对于包含文字的数字图像,通常会表现为本应光滑的字母边缘出现锯齿。对于数字音频而言,失真意味着采样后的声音中出现原本并不存在的声音频率。
奈奎斯特定理规定,对于要采样的数据,如果其频率范围是有限的,要从采样后的数据中无失真的复原信号,那么采样评论必须大于2倍最高待采样的信号频率。对于要采样的数据,其最高频率的2倍称为奈奎斯特频率。1928年奈奎斯特提出关于采样率的理论,在1949年该理论被克劳德.香农证明和扩展,因为这个原因,这个定理有时称为奈奎斯特-香农定理。
奈奎斯特定理对于图像采样仍然适用,图像在二维空间上重复的速率也可以使用空间频率描述。
3.4 量化、量化误差和信噪比
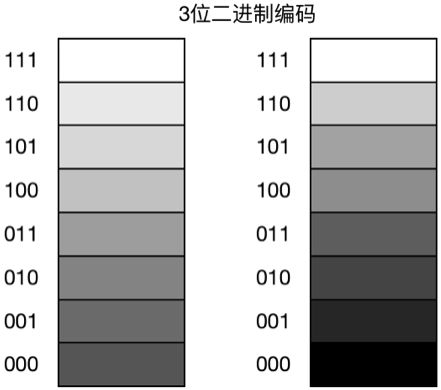
模数转换的第二步就是量化,首先我们需要知道样本是如何在在计算机中表示的。对于数字图像,二维图形上的每个样本表示一个离散点的颜色。表示的颜色数量取决于每一个样本的位数,即样本大小或者位深度,有时也称为颜色深度。通常用24位表示由RGB(红、绿、蓝)颜色空间描述的颜色,能表示的颜色数量为2的24次方种颜色。
对于数字音频,每一个样本表示声波在离散时间点上的振幅。通常的样本大小为8位或者16位。立体声CD品质数字音频有2个16位的声道组成,即共需要32位。
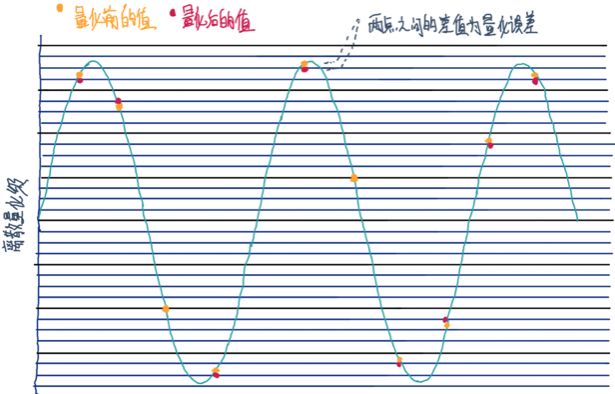
对于数字图像,样本大小影响了与原始色彩的相似度,对于数字音频,样本大小影响了波形中需要保留的振幅精度。如下图所示,在时间域上以某个采样率采样,样本值只能取离他最近的离散值,它的实际值和取整值之间的差值称为量化误差。
量化误差可以使用信噪比(Signal-to-Noise Ratio,SNR)来衡量,信噪比的基本定义为信号中有语言的内容与附带的噪声的比值。在模拟数据通信领域中,定义为信号的平均功率与噪声的比值。对于数字图像和声音,信噪比定义为最大样本值与最大量化误差的比值,又称为信号-量化噪声比(Signal-to-Quantization-Noise Ratio,SQNR)。其无量纲单位为分贝,dB,用于描述相对功率或者相对强度。其定义如下。
分贝也可以用振幅来表示,其定义如下。
对于数字图像、数字音频,对于线性量化样本时,分贝还可以使用量化时的位深度来表示。信号量化噪声比的值与位深度呈正相关。其具体定义如下。
动态范围通常定义为最大振幅声音(对于图像来说是颜色)与给定位深度表示的最小值的比,其数值和位深度相关。显然,对于相同的动态范围而言,如果表示的颜色或者声音范围越大,相对而言其量化误差越大。
对于数字音频,在选择位深度时要考虑声音的类型,如对于管弦乐在高音和低音区都广泛分布,不宜采用过小的位深度,即不宜使用过小的动态范围。
4 数据存储
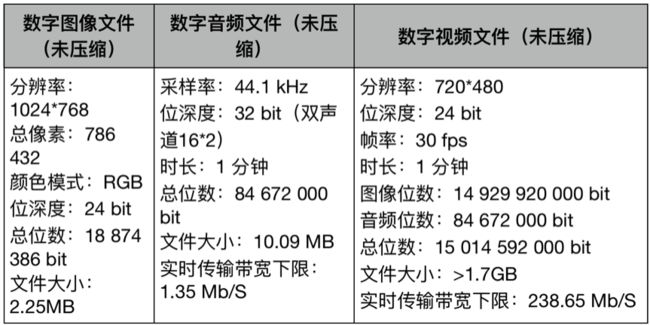
数字媒体文件在无压缩时,其文件大小十分庞大,如下表所示。对于一张容量为17GB的DVD,也只能装下使用下表编码参数的11分钟未压缩视频。因此数字媒体的压缩十分重要。
5 数据通信
通常我们会讲数字文件发布到网上,此时我们必须考虑数字数据传输媒体和通信方法。另外捕获实时声音和视频要求数据传输保持与数据播放相同的速度,这个问题的核心点是网络环境的带宽和媒体文件的码率。此外,想要弄清手机上播放的视频和电视节目的区别,我们需要了解模拟通信和数字通信的区别和联系。
5.1 模拟数据通信和数字数据通信
数据的通信方式分为模拟数据通信和数字数据通信,区分的标准是传输的数据类型是模拟数据还是数字数据,不能将传输的介质如卫星、电缆、广播作为评判的标准。
如下图,模拟数据通信传输的是连续的模拟信号,如连续变化的声音信息和图像信息,在电缆上传输时表现为连续的电压信号。
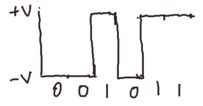
如下图,数据数字通信传输的是离散的数字信息,如使用0和1编码的数字音频和数字视频,在电缆上传输时表现为连续的电压信号。
上图将电压划分为两个离散等级的方法称为系带传输,发射器和接受器之间的通信线路称为系带通道。
基带传输是通过电线和同轴电缆进行的,它只在短距离传输中工作较好,噪声和衰减导致信号在通信通道传输中降幅。基带传输并不是唯一,也不是最常用的数据通信方式。另外一种选择是调制数据传输,也称为带通传输。它是基于缓慢降幅的连续震荡,因此有利于远距离通信。调制传输将需要传输的数据合成到一个基础频率的波之上,再将合成后的波传输,这个基础频率波称为载波信号。
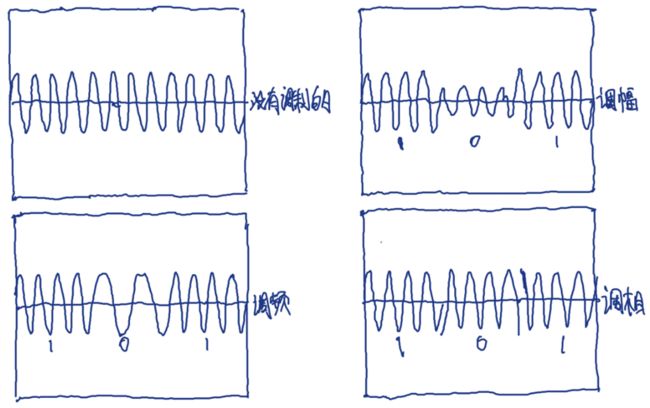
调制载波的三种基本方法分为调幅、调频和调相。下图演示了数字信号101的调制原理。必须注意的是,调制的信号不一定是数字化的,载波频率和调制用于传输模拟无线电和电视信号已经有很长时间了。
当有数字1传输时,在调幅中,载波信号的振幅会增大一个固定值;在调频中,其频率会发生变化;在调相中,其相位会发生变化。遗留问题RichardJieChen,这里调频和调相似乎都会降低数据的传输速率,需要再细看。另外,对于调幅调制,在后续文章视频信号的表示中会详细讲到。
在带通传输中,载波信号加在频带(也称为频道或者通道)的中间用于通信。发送器和接收器都知道分配给它们的频道,发送器只使用这些频道中的频率来发送信息,接收器只监听频道中的通信。
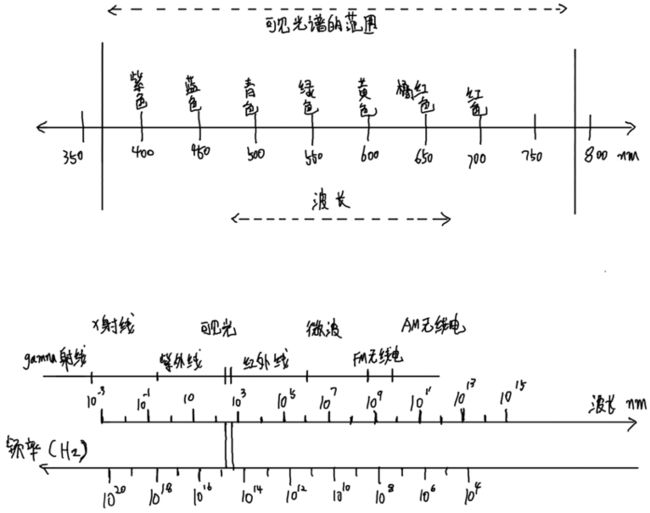
光纤通信,以及卫星、收音机使用的电磁波通信,都利用载波信号进行带通传输。不同颜色的光有不同的频率,在光纤通信时它们可以划分为不同的频带。模拟信息和数字信息都可以用光或其他电磁波形式的载波信号进行编码,调制成包含所要发送的信息。
可见光谱的频率分布,和电磁波的频段分布见上图。
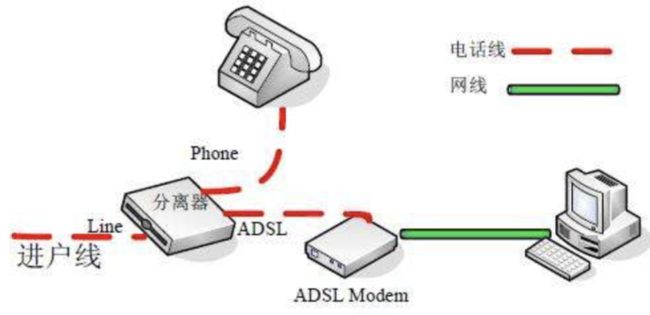
一个连续震荡的电压也可以作为载波信号,这个事实使得电话系统处理数字数据成为可能。最初电话系统通常被设计成以模拟形式进行通信,当调制解调器出现后,通过电话线上网也成为可能。
调制解调器代表了调制器和解调器,它能接收来自计算机的数据,使用前文所讲到的调频、调幅和调相中的某一种方法,将0和1这种数字信号写入到连续的震荡电压中;在通信的另一端,另外一个调制解调器将信号传输给另一台计算机。一个简单的使用电话线上网的示意图如下。
负责研究和改进基带传输和带通(调制的)通信的组织有,国际电信联盟(International Telecommunication Union, ITU)、电气和电子工程师协会(Institute for Electrical and Electronic, IEEE)、和电气工业协会(Electronic Industries Association, EIA)。
小结
- 模拟数据和数字数据都可以通过铜线、同轴电缆、光纤和自由空间进行传输。传输介质不能确定通信时模拟的还是数字的,只能通过数据的形式确定。
- 数字数据可以通过基带信号或者带通(如调制)信号进行传输。基带信号使用0和1的离散脉冲。调制信号使用载波频率和基于周期性改变信号频率、振幅或者相位编码数据。
- 模拟数据和数字数据通可以通过同一种调制信号传输。载波信号可以调制成包含模拟数据或者数字数据。
5.2 带宽
在数字通信中带宽用于描述最大变化速率
在讨论这一小点之前,需要明确一个前提条件,这里我们仅仅讨论0和1的数字信号传输。该传输可以是通过离散脉冲,也就是基带传输中离散的电压变化。也可以通过载波信号的频率、振幅或者相位变化来传输。带宽在此语境下指的是信号改变得有多快。
对于基带传输而言,指的是信号电压从V变化到-V的速率有多快,而对于带通传输,带宽描述到是改变载波信号得振幅、或者频率、相位的速度有多快。
带宽的高度受限于发送装置的改变能力,受限于传输介质的处理信号衰减和错误的能力,也受限于接收装置的识别能力。整个系统最大的变化速率称为该系统的带宽。
例如位于海上的两艘船需要手电筒的灯光闪烁用于莫尔斯密码交流时,信号交流的速度取决于手电筒开启和关闭的速率有多快;也取决于两人之间的天气是暴雨还是晴天,因为这会干扰信号的传输;也取决于接收信号的人能够以多快的速率来识别这些信号。
带宽的单位是周期每秒(赫兹),1Hz表示传输系统在1s内能够把电压水平改到另外一个电压水平再改回来。这意味着一个具有5000Hz带宽的基带传输系统每秒能传输的数据为10000位。
假设信号以两种可能的信号级合b赫兹的带宽发送,那么数据的传输速率d(位每秒)满足公式:d = 2 bit/s。传输系统编码的信号级多于两个时称为多极编码,如4个电压等级时可以分别编码位00、01、10、11。电压等级受到硬件识别信号的能力限制,通常不会太多。
假设信号以k种可能信号级合b赫兹的带宽发送,那么数据传输的速率d(位每秒)满足如下公式。
用频率定义的信号的带宽
数据传输中的信号都可以抽象位波的形式,而任何复杂的周期波形都能分解为不同频率的简单正弦波分量。对于任意一个信号,其分解后的最高频率分量位fmax,最低频率分量位fmin,那么信号的带宽表示位w,并且w = fmax - fmin。
对于带通传输而言,当信号在某个频道上传输时,信号的带宽必须符合频道的宽度,否则部分信息将会被丢失。频段的宽度越大,该频道内每秒允许传输的数据量越大,该点的具体原理在后面分析数字视频时会详细展开。
用频率定义的通信频道的带宽
当数据经过调制后通过电波传输时,它们都是在某一个频道内通信,频道内的频率范围一起构成了频道的带宽。通常载波信号为该频道的中心频率,而频道的最高频率减去最低频率的差值称为通信频道的带宽,也称为通信频道的宽度。
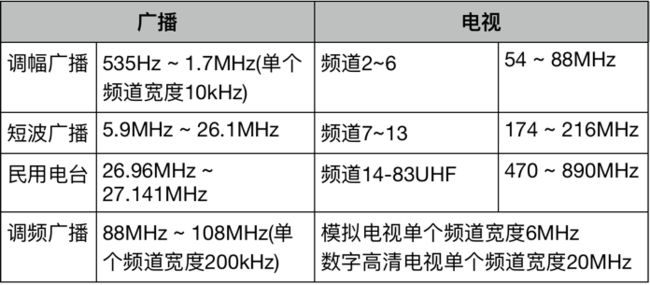
对于数字和模拟信号,数据在传输时,调制增加了原始载波信号的频率分量,成为边带,这些边带必须位于指定的频道内。美国联邦通信委员会(Federal Communication Comission)对通信频道划分如下。
对于如何为调幅广播、调频广播、电视和数字高清电视划分一个合适的带宽;载波信号的调制怎么样引起的边带;边带的频率时多少;它们时怎样影响频道的带宽要求?这些问题将在数字视频部分的内容详细讨论。
5.3 数据传输速率
位速率
带宽经常被随意的直接用于表示位速率,但是需要注意的是带宽的单位是周期每秒(Hz),二位速率的基本单位是位每秒(bit/s)。与位速率相关的单位如kb/s和b/s之间的进位规则位10的三次方。
理论上位速率和带宽的公式为“d = 2b*log(2)(k)",其中k表示能传输的不同信号值的数量。由于通信系统中存在如电磁干扰等噪声干扰,接收者不能总是正确的翻译信号,这个值在现实中几乎不可能达到。
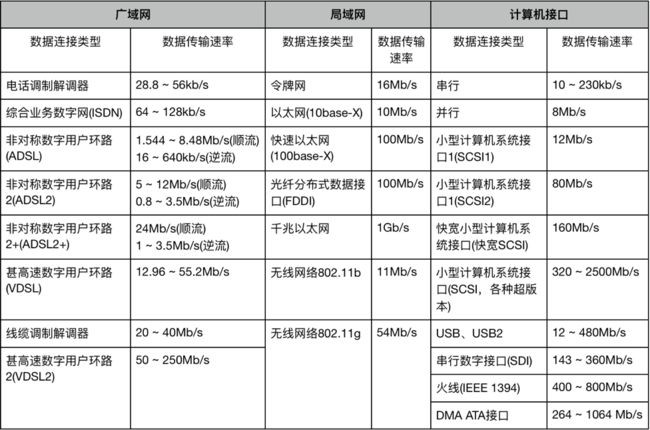
香农定理量化了含有噪声的传输系统所能达到的数据传输率“c = b*log(2)(1+s/p)"。其中c表示通信系统支持的最大传输速率,s表示信号的功率,p表示噪声的功率。在这里s/p是前文提及的信噪比的另外一种用法。数据传输的速率源于信号在给定传输介质中的变化情况,它与系统的信噪比有很大的关系。一些常见的网络类型和它们对应的传输速率如下表,这个速率可能会更新。
波特率
波特率最精确的定义是:它是发送和接收装置的一个性质,描述信号每秒的变化数量。但是在实际使用时,该定义使用比较随意,电话调制解调器的波特率常被描述为位每秒,而不是周期每秒。
- 因为带宽和数字数据通信相关,因此波特率和带宽的意义接近。不同点在于波特率通常在涉及发送和接收装置时被用到,而带宽在提到电波频道时还有其他意义。
- 一个装置(如调制解调器)有最大的波特率和实际波特率。实际波特率就是发送者和接收者之间对一个特定通信商定的速率。
- 经常提到的波特率实际上是位速率。
6 压缩方法
在保存数字媒体文件时,原始数据过大必须进行压缩。在压缩过程中需要尽可能的减小文件的体积,同时也要尽可能维持图像、音频和视频的质量。从压缩后的质量维度看,压缩类型可以被分为有损压缩和无损压缩。从算法实现的维度看,压缩类型分为基于词典、熵、算术、自适应、感知和差分的压缩方法。
- 基于词典的方法(如LZW压缩)使用固定长度代码的查询表,在压缩文件中,一种代码可能对应的一串字符而不是单个字符。
- 熵压缩使用字符频率的统计分析,使用更短的码字对应频繁出现的字符进行编码实现压缩。每个码字对应一个字符,如香农-法诺和哈夫曼编码。
- 算术编码也使用了一个类似的统计分析,但是使用的是单一的码字对一个文件进行编码,而不是为每个字符创造一个单一的码字。
- 自适应方法在压缩文件的过程中获取关于文件性质的信息,然后调整编码使之反应每一步所学到的东西。如LZW压缩,代码表是在压缩和解压缩的过程中即时创建的。如果哈夫曼编码随着压缩过程频率数进行更新而不是事先搜集,也是自适应的。
- 感知编码是根据心理学模型删除不敏感的信息。它被广泛用于数字媒体工程中。
- 差分编码通过计算信号的变化进行编码。也被广泛用于数字媒体工程中。
压缩算法的压缩率是原始文件的大小a与压缩文件大小的比,表示位a:b。或者表示为b对a的百分比。如对于被压缩到原始文件一半的文件,其压缩率可表示为50%或者2:1。
6.1 游程编码
游程编码(Run-Length Encoding, RLE)属于无损压缩,应用于图像压缩。如带有.bmp后缀的图像文件可以选择使用游程编码。它不存储单个像素的值,而是存储数偶(c,n)。其中c表示灰度值,n表示连续像素c的个数。
对于如下图所示的一行像素,从左至右每个像素的灰度值分别为255,255,255,255,255,255,242,242,242,242,238,238,238,238,238,238,255,255,255,255。其游程编码为(255,6),(242,4),(238,6),(255,4)。
此时可以看出未使用游程编码时,该行像素需要20个字节存储。而使用游程编码后,存储的大小由数偶所需的字节数决定。对于数偶(c,n),c的取值为0~255,使用1个字节编码,而n的编码长度由其取值范围决定,假设其取值范围为0~r,则其所需字节b满足如下公式。
因此对于像素尺寸为100*100的图片,假如最大连续像素为300,n的编码长度通过计算为2字节,因此使用游程编码时只需要12字节就可以存储同样的像素行。
需要注意的是游程编码并不一定会减少文件体积,如对于如下像素行进行游程编码。其原始的灰度值为255,255,255,255,243,240,242,242,242,241,238,238,237,237,237,237,255,255,255,255。共占20个字节的内存资源。而其游程编码为(255,4),(243,1),(240,1),(242,3) ,(241,1),(238,2),(237,4),(255,4),共占24个字节内存资源。
实际使用中,通常会指定r的位深度,当连续的像素数超过r能表示的长度时则截断表示为下一个数偶。如对于1000个连续的灰度值为255的白色像素进行编码时,当位深度指定为8时,其游程编码为(255,255),(255,255),(255,255),(255,235)。
下图是一个使用游程编码的很好例子,不考虑文件头信息,其包括100乘100 = 10 000个像素,需要10 000个字节存储,当使用游程编码时仅需要1084个字节,压缩率为9:1,约为11%。
显然,大部分图像并不会如此颜色分明,因此游程编码适用于图像区域分割鲜明,颜色类型有限的卡通图片。这里仅说明游程编码的基本原理,实际实现时会略有不同。
需要注意的是对于任意一种无损压缩算法和任意长度的文件,至少存在一种情况使得算法不能减少文件的体积。推导过程如下。
- 假设文件长度为n位,那么不同的文件有2的n次方个。
- 假设某个无损压缩的算法,输入长度为n的文件,输出长度<= n-1的压缩文件。那么可以生成1+2+4+...+2的n-1次方 = 2的n次方 - 1个不同的压缩文件。
- 要将2的n次方个文件对应2的n次方-1个不同的压缩文件,显然无法一一对应,即无法从1个相同的压缩文件还原到2个不同的原始文件。
无损压缩算法应用于不允许数据丢失的情况。例如对文本和二进制编码的计算机程序进行压缩的情况。应用于像gzip和compress(UNIX)平台、或者pkzip和winzip(Windows平台)这样的工具中。声音文件几乎不会出现相同数值连续的音频数据,不适用于无损压缩。图像文件如PNG、TIFF文件都支持无损压缩。
6.2 熵编码
克劳德.香农(Claude Shannon)指出通过熵编码可用获得更好的压缩率。熵编码是通过可变字长编码的工作方式,用更少的位编码出现更频繁的字符,同时用更多的位编码罕见的字符。
借助物理学中的术语熵,香农(Claude Shannon)定义了信息源的熵。S是一串字符,经处理后描述为有n个不同字符组成的字符串S‘,pi是字符串S‘中第i个字符的频率。则S的熵H(S)满足如下公式。
应用香农熵公式,可以根据每个字符出现的频率来确定一串字符中每个字符实例所需平均位数的一个最佳数值。香农证明了当字符串S的平均编码长度为H(S)时能够得到最佳的编码效果。
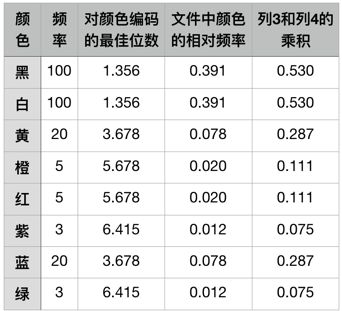
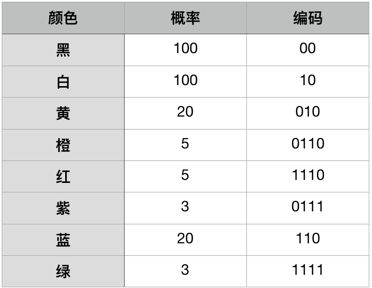
对于一个含有256个像素的图像文件,其像素的颜色频率统计如下。
使用香农熵公式可计算出,该图像文件的熵为2.006,意味着在一个最佳的压缩文件中,表示每个字符的平均编码长度为2.006。
香农-法诺算法的实现如下。
该算法采用自上向下递归的方法,每一次递归将字符分为两半,两部分的频率和近似相同。最后生成一个编码树,树枝用0和1来标记,从根节点到叶节点遍历,并记录所有的0、1序列,得出与叶节点相关的字符代码。
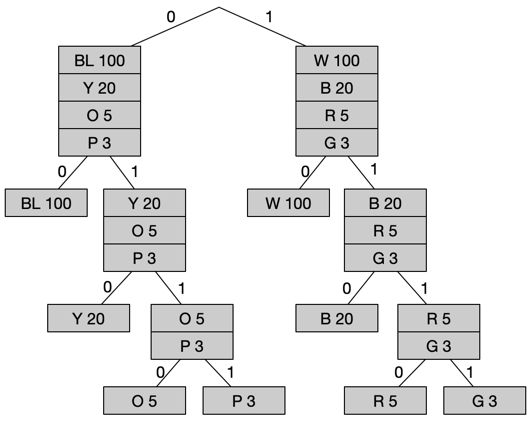
前文对于一个含有256个像素的图像文件的例子,经过香农-法诺算法处理可以得到如下一颗树。未用任何算法处理的原始文件体积为2048位,而经过香农-法诺算法处理后的文件仅需要584位,文件的压缩率为28%。平均每个字符的编码长度为2.28位,这和香农-法诺算法计算出的熵很接近。
上述实例的颜色编码表如下。
熵的通俗定义是事物排列的多样性,如使用两个骰子掷出2点只有1种组合可能,而掷出7点有6种不同的组合方式,因此7这个值的熵比2这个值的大。当文件大小一定,其包含的符号数越多的时候,香农熵公式计算出的值越大。因为字符数越多,字符的排列组合也就越多,所以具有更大的熵。因此每个编码字符需要传递更多的信息,其平均编码字符长度更长。
对于数字媒体,熵编码基于被编码数据的统计分析。可以是某个实际文件的统计分析,也可以是某类型文件的通用统计分析。哈夫曼编码是一类特别的熵编码,它提高了香农-法诺算法的压缩率,在图像压缩中非常有效。
6.3 算术编码
香农-法诺算法和哈夫曼编码的一个缺点是必须单独处理每个字符,而每个字符有它自己的编码,这些编码的长度都是整数位。香农公式表明可以用非整数位编码来获取最佳的编码,如使用1.3561位来表示黑色和白色。
算术编码克服了上述缺点,和香农-法诺算法类似,算术编码也基于文件中字符频率的统计分析。不同之处在于它不再是位单个字符创建编码,而是对整个文件进行编码,从而获得更大的压缩率。
在算术编码中,用简单的浮点数对一串字符进行编码,理论上,为了满足压缩的要求,可以使用任意位的浮点数,这意味着其有无限精度,但是显然这不现实。这里先不考虑该问题,只关注算术编码实现的理论基础。
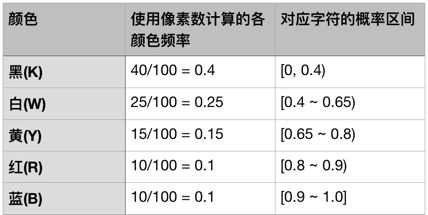
假设一个图像文件包括100个像素,共黑(K)、白(W)、黄(Y)、红(R)、蓝(B)5种颜色,其每种颜色的的频率统计如下。需要注意的是,只要编码器和解码器使用相同的颜色顺序,则概率区间内的颜色顺序并不重要。
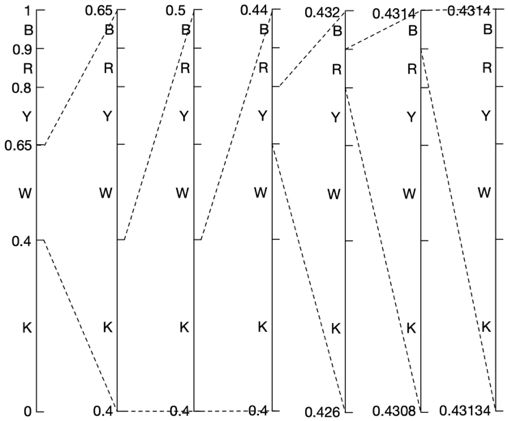
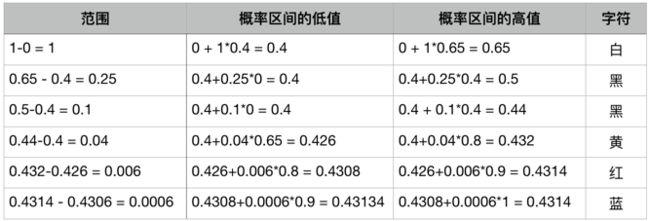
现在考虑原始的概率区间文件[0,1],对图像前6个像素白、黑、黑、黄、红和蓝进行编码。
- 第一步,计算出当前范围为1,需要编码白色像素,因此编码后概率区间更新为[0+1乘0.4, 0+1乘0.65],为[0.4, 0.65]。
- 第二步,计算出当前范围为0.25,需要编码黑色像素,因此编码后概率区间更新为[0.4+0.25乘0, 0.4+0.25乘0.4],为[0.4, 0.5]。
- 第三步...
- 最后得到算术编码的区间为[0.43134, 0.4314],编码字为(0.43134+0.4314)/2 = 0.43137。
用图像的方式可以将计算过程表示如下。
用表格的方式可以将计算过程表示如下。
其简单的算法实现伪代码如下。
algorithm arithmetic_encoding
/* Input: A string of symbols and their assigned probability intervals.
Output: A floating point number that encodes the string*/
low = 0.0
hight = 0.0
while input symbols remain {
s = the next inputs symbol
range = high - low
/*s_high(s) represents the high value of symbol s's assigned probability interval,
and s_low(s) represents the low value of symbols's assigned probability interval.*/
high = low + range * s_high(s)
low = low + range * s_low(s)
}
return (low+high)/2
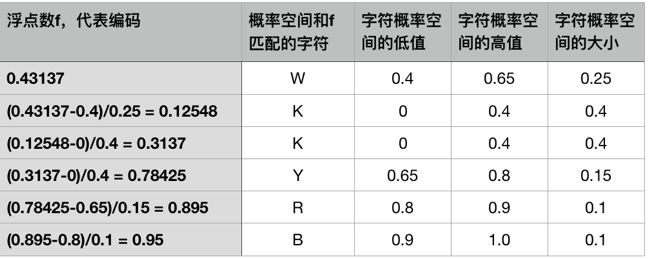
在解码时,给定一个浮点数a。
- 可以从初始概率范围开始,通过寻找浮点数适合的概率区间得到编码字符串的第一个字符。如前面的例子编码为0.43137,可以得出第一个字符c1的符号为W。
- 设下一个浮点数为b,利用公式b = (a - c1low) / c1range。其中c1low表示字符c1点概率空间低值,c1range表示字符c1的概率空间范围。
- 此时b计算出为0.12548,可以得到第二个字符c2的符号为K。
- 不断的重复前两个步骤,直至解码到终止标志,则可以得到原始的字符串。
用表格的方式可以将解码计算过程表示如下。
其简单的算法实现伪代码如下。
algorithm arithmetic_decoding
/*Input: A floating point number, f, encoding a string of symbols, a list of symbols
encoded by the number, and the probability intervals assigned to these symbol.
Output: The string of symbols, s, decoded
Assumptions: A terminator symbol has been encoded at the end of the string */
symbolDecoded = NULL
while symbolDecoded != TERMINATOR_SYMBOL {
s = a symbol whose probability interval contains f
output s
/* Let s_high(s) represent the high value of symbol s's probability interval, and s_low(s)
represent the low value of s's probability interval*/
range = s_high(s) - s_low(s)
f = (f - s_low(s)) / range
}
在实际实现算术编码时,使用整数运算和移位运算,不需要使用无限精确的浮点运算。怎样终止输入字符串和怎样加速费时的压缩方法需要去具体的实现中了解,这里需要注意算术编码可以用于JPEG图像压缩中的一个步骤,另外IBM等公司对该算法享有专利权。
6.4 变换编码
前面提到的编码算法都是无损压缩,而下面将要提到的事有损压缩算法。变换编码通过改变数据的表示方式实现,最常用是离散余弦变换(Discrete Costine Transfer, DCT),和离散傅里叶变换(Discrete Fourier Transfer, DFT)。需要注意的是变换编码自身不是有损变换,不会丢失数据。
有损压缩基于变换编码,它的思想是通过变换编码,使声音或视觉细节不被丢失,而丢失的部分超出了人类感知的范围。但是DCT和DFT中并不会有数据丢失,而是在后面的步骤中丢失部分冗余的、或者不重要的信息。这就是有损压缩中损失的那部分。
离散余弦变换用于数字图像,将数据表示从空间域改变到频域。而频域内的高频分量可以理解为在一个很小空间内颜色的快速波动,这些变换人眼很难察觉,可以直接删除。这就是JPEG压缩的理论基础。
离散傅里叶变换用于声音,将它从时间域变换为频域。而频域空间内,由于人类听觉的生理特征决定某些频率分量会屏蔽其他频率分量的感知,因此丢弃被屏蔽的频率分量可以达到压缩音频的目的。这也是MPEG标准中音频压缩的理论基础。
6.5 压缩标准和编解码器
前文仅仅介绍了各个压缩算法的理论基础,实际上,压缩算在具体实现时都会有细微的改变和优化。在图像、音频、视频的压缩标准中,都会结合多种算法。如JPEG和MPEG压缩结合了DCT、可变字长编码和哈夫曼编码用于图像的压缩。
有些算法被官方委员会标准化从而使得各种各样的实现能够生成相同格式的文件,如果一个标准化的算法获得了专利,那么商业公司必须支付一定的许可费来实现该算法,然后以商业产品卖掉。标准化压缩算法的两个突出例子是用于数字视频摄录的DV和MPEG算法家族。算术编码也是专利涉及图像压缩的一个例子。
压缩算法的具体实现称为编解码器,即压缩/解压缩的简称。有些编解码器作为共享或者免费软件提供。但是大多数编解码器是商业产品。它们可以嵌入图像、音频或者视频处理程序,或者单独出售和使用。如QuickTime中嵌入了标准Sorenson编解码器。
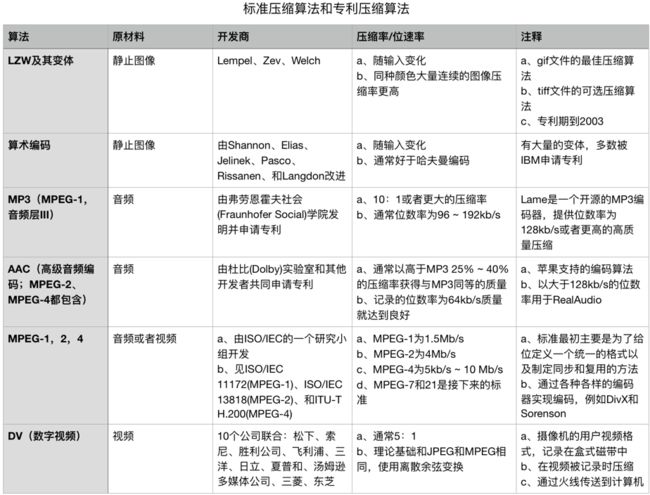
大多数编码器,用户可以通过设置码率、或者质量等级设置压缩率。压缩率越高,与原始的资源相比质量损失程度可能越大。对于视频而言,生成的文件大小只和视频的码率、以及视频的时间相关。下表列出了常见的标准压缩算法、专利算法。
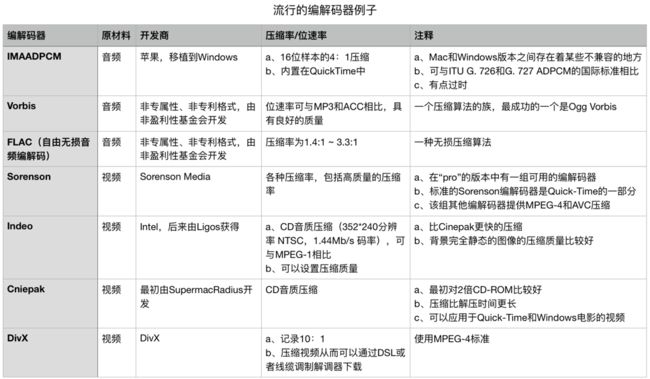
下表列出了流行的编解码器。
6.6 数字媒体的标准和标准化组织
标准可以分为三种主要类型:专有的、事实的和官方的。专有标准由商业公司建立并申请专利,如LZW压缩和算术编码。事实标准描述一种方法或者格式,这些方法已经被行业认可,但是没有任何官方认可,如TIFF图像文件。官方标准由大的产业联盟和政府机构一起开发,如MPEG标准。
在多媒体的研究中,将会认识到制定标准的组织和工作小组,因此需要熟悉他们的名字和首字母缩写词。国际电信联盟(International Telecommunication Union, ITU), 前身为CCITT。ITU是协调全球电信网络和服务的组织,如分配无限的频带。和多媒体相关的是G和H系列,G系列覆盖语音编码和电话通信,如G.700系列涉及使用ADPCM(自适应差分脉冲编码调制)模拟数字电话的编码。H系列属于实时数字音频和视频通信领域,如H.323是一个声音和视频分组标准(交换网络,如因特网),H.262给出了MPEG压缩的标准。
国际标准化组织(International Organization for Standardization, ISO)开发了行业和商业标准,它是由来自各个国家标准组织的代表组成。
国际电工委员会(International Electrotechnical Commission, IEC)制定电气、电子和相关技术标准。
IEC和ISO有一个联合委员会,称为ISO/IEC JTC1。该委员会开发了信息技术标准。如ISO/IEC 11172标准定义了MPEG-1,ISO/IEC 13818定义了MPEG-2。
7 傅里叶变换
图像、音频和视频进行有损压缩时都依赖于变换编码,而变换编码的数学理论基础为傅里叶变换,因此想要深入了解多媒体的编码原理,必须熟悉傅里叶变换。
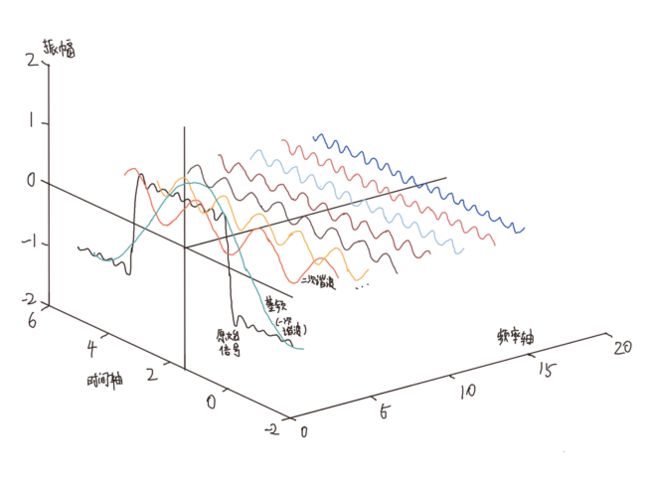
如下图的上部分,随着时间记录表示音波的震动幅度(也可以理解为空气压强),我们可以得到一个音波在时域的函数。而傅里叶变换可以通过将时域的函数分解为基础的余弦函数,从而将时域的函数转换为在频域的函数,如下图的下部分。
7.1 傅里叶级数
傅里叶变换的衍伸变换都可以从傅里叶级数开始推导,傅里叶证明任何周期函数都可以使用无穷的正弦波叠加,如下图。
傅里叶变换的公式表示如下。需要注意的是只有当周期函数f(t)满足分段连续、分段单调、绝对可微的条件时,该函数满足狄利克雷条件,它才可以表示为傅里叶级数。
在开始证明傅里叶级数之前,我们需要了解三角函数系正交性,如下。下图左侧为公式,右侧为举例推证。
因此傅里叶级数的推导过程如下。第一步不用证明,这是傅里叶证明过的。
傅里叶级数更为常见的公式是通过自然常数e来表达的,其推导过程如下。
7.2 傅里叶变换
傅里叶级数将连续时域函数转换为离散频率函数,在此基础上推导的傅里叶变换能将连续的时域函数转换为连续的频域函数。其推导过程如下。
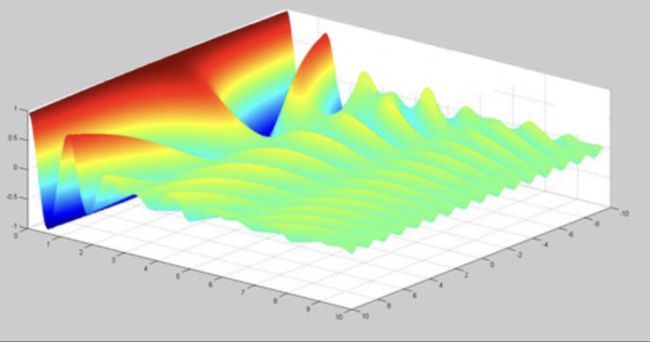
可以想象离散周期函数经过傅里叶变换后,在频域图上的无穷多简单波形可以组合为泛着波纹的海面。如下图。
7.3 离散傅里叶变换
在图像和音频采样过程中,我们获取到的样本点在时域上都是离散的,因此我们需要一种新的数学模型。而傅里叶的推导离散傅里叶变换能将离散时域的函数转换为离散频域的函数。其推导过程如下。
7.4 离散余弦变换
二维离散余弦变换时JPEG图像压缩的重要理论基础,这里仅介绍如何从离散傅里叶变换推导出一维离散余弦变换(DCT)。一维DCT实际上是对N个样本的DFT的对称扩展。即将样本值[f0, f1, f2, ... fn-1]对称变换增加N个样本值[-f(n-1), -f(n-2), ... -f0]。但是需要注意的是离散余弦变换丢弃了各个频率分量的相位信息,因此不能用于音频处理。
对称变换一维DFT的过程如下图所示。
一维离散余弦变换的推导过程如下。周期变为2N后,函数的系数有1/N未变为1/2N的原因还需要查明。