1. 基本概念
比如:输入N个字符串,我们需要找打最大的M个字符串。我们可以将N个字符串进行排序,然后取最大的M个。也可以将新的输入和已知的M个最大字符串进行比较。只要我们用优先队列能高效的实现insert()和delMin()就能解决该问题。
public class TopM {
// This class should not be instantiated.
private TopM() { }
/**
* Reads a sequence of transactions from standard input; takes a
* command-line integer m; prints to standard output the m largest
* transactions in descending order.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
int m = Integer.parseInt(args[0]);
MinPQ pq = new MinPQ(m+1);
while (StdIn.hasNextLine()) {
// Create an entry from the next line and put on the PQ.
String line = StdIn.readLine();
Transaction transaction = new Transaction(line);
pq.insert(transaction);
// remove minimum if m+1 entries on the PQ
if (pq.size() > m)
pq.delMin();
} // top m entries are on the PQ
// print entries on PQ in reverse order
Stack stack = new Stack();
for (Transaction transaction : pq)
stack.push(transaction);
for (Transaction transaction : stack)
StdOut.println(transaction);
}
}
2. 堆的定义
定义:当一颗二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序。根节点是堆有序的二叉树中的最大结点。
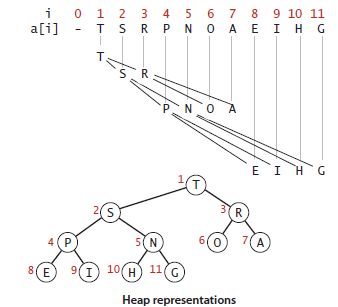
堆的表示:
①按照树的层级结构来存储
②不使用数组中的第一个位置。
③一颗大小为N的完全二叉树的高度为lgN向下取整。当N的数量达到2的整数次幂时树的高度加1
④位置k的结点的父节点是⎣ k/2⎦ ,子节点分别为2k或2k+1
高度=⎣ lg 11 ⎦ 向下取整=3
3. 堆的算法
我们用长度为N+1的pq[]来表示一个大小为N的堆,不使用pq[0]。
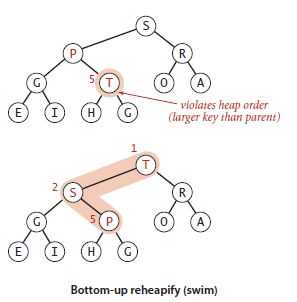
①由下至上的堆有序化(上浮)
某个结点比自己的父结点更大,交换它和它的父节点,直到满足堆有序。
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
② 由上至下的堆有序化(下沉)
某个结点比它的两个子结点或是其中之一要小,将它与两个子节点中较大的值进行交换,直到保证堆有序。
private void sink(int k) {
while (2*k <= n) {
int j = 2*k;
if (j < n && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
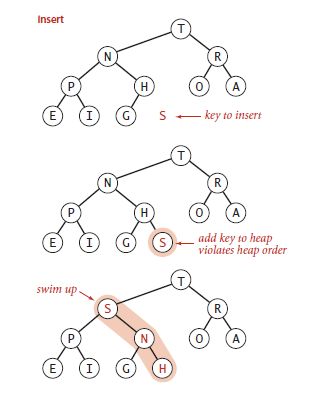
③ 插入元素
将新的元素添加到数组末尾,增加堆的大小,不断上浮
④ 删除最大的元素
从数组顶端删除最大的元素,并将数组的最后一个元素放到顶端,减小堆的大小,并让这个元素下沉到合适的位置。
⑤ 基于堆的优先队列
public class MaxPQ>
{
private Key[] pq; // heap-ordered complete binary tree
private int N = 0; // in pq[1..N] with pq[0] unused
public MaxPQ(int maxN)
{ pq = (Key[]) new Comparable[maxN+1]; }
public boolean isEmpty()
{ return N == 0; }
public int size()
{ return N; }
public void insert(Key v)
{
pq[++N] = v;
swim(N);
}
public Key delMax()
{
Key max = pq[1]; // Retrieve max key from top.
exch(1, N--); // Exchange with last item.
pq[N+1] = null; // Avoid loitering.
sink(1); // Restore heap property.
return max;
}
// See pages 145-147 for implementations of these helper methods.
private boolean less(int i, int j)
private void exch(int i, int j)
private void swim(int k)
private void sink(int k)
}
⑥性能分析
长度为N的基于堆的优先队列,插入元素操作只需要不超过lgN+1次比较,删除最大元素操作,不超过2lgN次比较(确定是否上浮和确定子结点中的最大值)。
4. 索引优先队列
可以当做:能够快速访问其中最小元素的数组。you can think of an IndexMinPQ named pq as representing a subset of an array pq[0..N-1] of items. Think of the call pq.insert(k, item) as adding k to the subset and setting pq[k] = item and the call pq.change(k, item) as setting pq[k] = item。
问题:多个有序的输入流如何归并成一个有序的输出流?
public class Multiway {
// This class should not be instantiated.
private Multiway() { }
// merge together the sorted input streams and write the sorted result to standard output
private static void merge(In[] streams) {
int n = streams.length;
IndexMinPQ pq = new IndexMinPQ(n);
for (int i = 0; i < n; i++)
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
// Extract and print min and read next from its stream.
while (!pq.isEmpty()) {
StdOut.print(pq.minKey() + " ");
int i = pq.delMin();
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
}
StdOut.println();
}
public static void main(String[] args) {
int n = args.length;
In[] streams = new In[n];
for (int i = 0; i < n; i++)
streams[i] = new In(args[i]);
merge(streams);
}
命令行:java Multiway m1.txt m2.txt m3.txt
A A B B B C D E F F G H I I J N P Q Q Z
% more m1.txt
A B C F G I I Z
% more m2.txt
B D H P Q Q
% more m3.txt
A B E F J N
关键:将多路输入和索引相关连,每次都从删除最小的元素的输入流中继续添加元素。
5. 堆排序
①堆的构造
方法1:构造N个元素的堆,从左至右依次将每个元素添加至数组的末尾,然后不断的上浮,直到将N个元素都添加至堆中。NlgN
方法2:从右至左不断下沉构造堆。
**利用下沉操作构建堆只需要2N比较和N交换。
②将堆中最大元素删除,然后放入堆缩小后数组中空出的位置
public static void sort(Comparable[] pq) {
int n = pq.length;
for (int k = n/2; k >= 1; k--)
sink(pq, k, n);
while (n > 1) {
exch(pq, 1, n--);
sink(pq, 1, n);
}
}
③分析
将N个元素排序,堆排序只需要少于2NlgN+2N次比较,以及一半的交换次数。2N来自于堆的构建,2NlgN来自于每次下沉操作最大可能次数。
堆排序是唯一可以同时利用空间和时间的方法,但是许多应用中很少使用它,原因是堆排序没有利用缓存,数组元素很少和相邻的其他元素进行比较,因此缓存未命中的次数远远高于其它的算法(快速、归并、甚至希尔)